Minimax algorithm

Minimax is an algorithm which can be used for two-player zero-sum game theory, in particular to program artificial intelligences.

Game tree

The states of the game can be represented by a tree, in which nodes are states, and one can navigate from one to another by playing one move.
Here is an example for Tic-Tac-Toe:

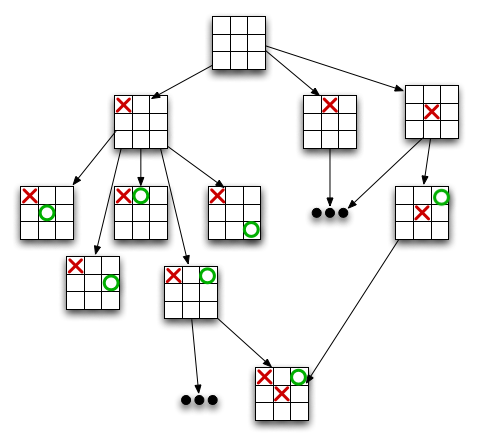
In theory it is possible to read the whole game by exploring the whole tree, to chose the best move to play, but those game trees are generally big. For instance, in the case of Tic-Tac-Toe the number of states is 2^9 = 512. Even though that's ok for a computer, it's already big for such a simple game. In comparison the size of a go board is 19x19, which corresponds to 2^361 states.

Evaluation function

Because the whole game tree cannot be explored, Minimax uses an evaluation function to estimate a state of the game. It takes a given state of the game as a parameter and returns a score.
If A and B are two players and the evaluation function is made from A's point of view, this means that the more the situation of the game is favorable for A, the greater the score should be. On the other hand, for a situation where A is likely to lose the score should be negative.
As it is supposedly a zero-sum game, if the score is X for player A, it will be -X for player B. The more player A is winning, the more player B is losing, and conversely.

When minimax is used for an artificial intelligence, its strength is essentially determined by the evaluation function. The way it works is arbitrary, and it usually needs some thought to implement. For instance, what is the score of this board?

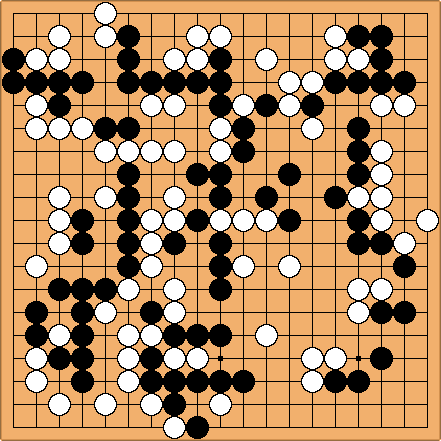
Not so easy, is it ?

Algorithm

Minimax explores a part of the game tree considering that for each step, each player plays the best move.
This means that for the moves played by A, Minimax will chose the state which has the maximum score, because it's the most favorable for A. On the contrary, Minimax considers that B will play the move which produces the state with the minimum score.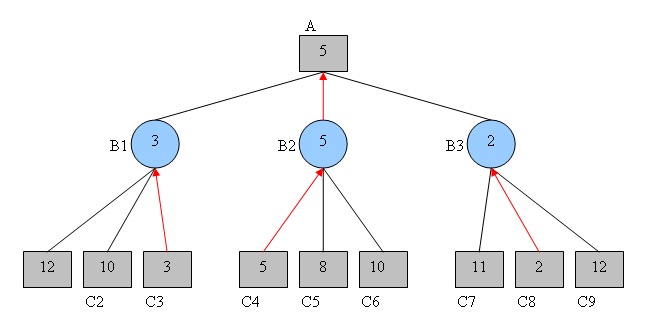
On this picture, squares represents states where A plays whereas circles are player B states.
If A plays the left move, B will be able to play three others, which would respectively result in states with scores of 12, 10 and 3. B wants to have the lowest score as possible so he will play the one which gives 3. So, if A plays the left move, the final score will be 3.
Using the same method for the other moves, one finds that the middle move is the best, because it is the maximum of the minima.

Depth of the tree

The exploration stops at a certain depth, chosen in advance. A deeper exploration gives better results, but takes more time.