LoginSignup
28
19

More than 1 year has passed since last update.

@M_Kotera(小寺 雅司)

高速で厳密なk近傍法(k-NN)の計算

Last updated at Posted at 2022-10-12

はじめに

本掲載について

こんにちは，NEC デジタルテクノロジー開発研究所 データ分析アクセラレーショングループの小寺です．
普段は機械学習を高速化する研究をしています．

高速で厳密なk近傍法(k-NN)の計算の研究をしていて一区切りつきましたので内容を共有したいと思います．よろしくお願いします．

k-NNは，データベースの中からクエリデータに対して最も近くにあるk 個のデータを選ぶアルゴリズムであり，回帰やクラス分類に使われる基本的なアルゴリズムです．
素朴な実装によるk-NNはモデル作成時に時間がかからず高速なものの，この実装によるk-NNを用いた分類や回帰は，データベース全体のデータを参照することから計算コストが高くなるという問題があります．
そこで，本掲載では入力データが6次元程度までの低次元に限りますが，Z-curveを用いることでk-NNの計算コストを減らす方法を紹介します．(基本的なアイデアは[1]を参考)

Z-curve

Z-curveは任意の精度で多次元空間を埋め尽くす空間充填曲線の一種であり，多次元データを1次元空間に写像することができます．
mojikyo45_640-2.gif
特に，Z-curveを用いてデータを多次元空間から1次元空間へと写像したとき，多次元空間上でのデータ同士の局所的な位置関係の情報を保持したまま写像することが可能です．
mojikyo45_640-2.gif
図のように多次元空間で近傍にあったデータは1次元空間でも近傍に写像されます．
また，多次元のデータを1次元のデータに写像したときの1次元の値をZ値といいます．多次元空間で近傍にあったデータのZ値は同じくらいの値を持ちます．
そして，Z-curveの重要な性質として多次元空間中の矩形において，始点(Z値の最も小さい矩形の頂点)と終点(Z値の最も大きい矩形の頂点)をZ-curveで結ぶと，そのZ-curveは矩形内部の全ての点を通ります．
mojikyo45_640-2.gif

以下ではZ値の紹介とその計算について紹介します．

Z値

Z値は多次元データを二進数表記にして互い違いにした値を10進表記にした値です．
例えば，多次元データが(23245, 35159)であったとします．(このときの多次元値は負の数でも浮動小数値でも計算は可能ですが簡単のため非負整数を用いています．)
この多次元データを2進数表記すると

(0101101011001101, 1000100101010111)

となります．
続いて，この2進数の値を大きい位の桁から順に交互に混ぜると，1次元目の数値(0101101011001101)の1番大きい桁の数は0，
2次元目の数値(1000100101010111)の1番大きい桁の数は1，1次元目の数値の2番目に大きい桁の数値は1，
2次元目の数値の2番目に大きい桁の数は0なので，0,1,1,0...と数は続き，これらを繋げると

01100010110010011011000110110111

という32桁の数を得ます．そして，この数を10進表記にするとZ値を得ることができます．
今の手順をまとめると以下のようになります．

  1. 多次元データを2進数表記する．
  2. 2進数表記された多次元データについて各桁の数を交互に混ぜる．
  3. 各桁の数を交互に混ぜた数を10進数表記する．

この文字列操作っぽいやり方でも，Z値を得ることができますが大量のデータを処理する場合，この方法では時間がかかるため，あまりおすすめできません．そこでbit演算によって高速化します．
(※数字を交互に混ぜ合わせる際に1次元目の数から混ぜたが，2次元目の数から混ぜ合わせても良い．)
(※多次元データからZ値を計算する際，Z値を多次元ベクトルとして表現することで多次元データに上限をつくることなく計算が可能になる．例えば，16bitの2次元データからZ値を作成するとZ値は最大32bitの数として表現される．Z値を16bitの2次元のベクトルとして表現することで実質的は32bitの数の表現が可能になる．)

以下ではZ値の計算(bit演算のイメージ)と，C++による具体的な実装を記載します．実装では多次元データの入力としてuint64_tを仮定しています．負の数，浮動小数点への拡張もreinterpret_castを使えば可能です．

Z値の計算

簡単のため16bitの計算で説明を行う．

多次元データ(23245,35159)について2進表記する．

(0101101011001101, 1000100101010111)\tag{0.0}

最終的に得たい1次元のZ値(2進数表記)は数式の多次元のベクトルとして

(0110001011001001, 1011000110110111)\tag{Z}

と表される．
以下では最終的に得たいZ値のうちの1次元目の数

0110001011001001\tag{Z_1}

を計算することを目標にする．

準備としてmask_bitを定義する．

\begin{align}
\rm{mask}_1=(0000111100001111, 0000111100001111)\\
\rm{mask}_2=(0011001100110011, 0011001100110011)\\
\rm{mask}_3=(0101010101010101, 0101010101010101)\\
\end{align}

2進数表記された多次元数(0.0)を8bit右にシフトする．

\begin{align}
0000000001011010, 0000000010001001\tag{1.0}
\end{align}

これで(Z_1)の計算を行う準備ができた．

最初に，(1.0)を4bit左にシフトする．

\begin{align}
0000010110100000, 0000100010010000 \tag{1.1}
\end{align}

次に(1.0)と(1.1)について論理和をとる．

\begin{align}
0000010111111010, 0000100010011001 \tag{1.2}
\end{align}

そして(1.2)とmask_1について論理積をとる．

\begin{align}
0000010100001010, 0000100000001001 \tag{2.0}
\end{align}

同様の操作を繰り返す．
(2.0)について2bit左にシフトする．

\begin{align}
0001010000101000, 0010000000100100\tag{2.1}
\end{align}

(2.0)と(2.1)について論理和をとる．

\begin{align}
0001010100101010, 0010100000101101 \tag{2.2}
\end{align}

(2.2)とmask_bit2について論理積をとる．

\begin{align}
0001000100100010, 0010000000100001 \tag{3.0}
\end{align}

(3.0)について1bit左にシフトする．

\begin{align}
0010001001000100, 0100000001000010 \tag{3.1}
\end{align}

(3.0)と(3.1)について論理和をとる．

\begin{align}
0011001101100110,  0110000001100011 \tag{3.2}
\end{align}

(3.2)とmask_bit3について論理積をとる．

\begin{align}
0001000101000100, 0100000001000001 \tag{4}
\end{align}

最後に(4)について1番目の数値を1bit左にシフトする．

\begin{align}
0010001010001000, 0100000001000001 \tag{5}
\end{align}

(5)について2つの数の論理和をとると所望の

\begin{align}
0110001011001001
\end{align}

を得る．

(Z)の2次元目の数

1011000110110111\tag{Z_2}

を計算する場合は下8桁の数を取り出すために，
(0.0)を8bit左にシフトした後16bit左にシフトすればよい．
その後(Z_1)の場合と同様の計算を行えば(Z_2)を得る．

32bit，64bitの計算や3以上の多次元数について計算を行う場合は，もう少し複雑な計算処理が必要になりますが，上記と同様の手順で計算が可能です．

実装

Z値の計算についての実装を計算します．
このコードではZ値の計算は6次元のデータまで載せています．任意の次元のデータに対してZ値を計算することが可能ですが，次元が大きくなるほどに多次元空間の距離情報が意味を持たなくなるために，この実装では6次元までしか載せていません．

Z値の計算

Z_value.cpp
std::vector<uint64_t> 
Z_value(std::vector<uint64_t> & input_vector, int&  input_vector_num, int&  input_vector_dim) {
  int init_data_shift = 64 / input_vector_dim;
  int morton_dim = input_vector_dim + (64 % input_vector_dim != 0); 
  std::vector<uint64_t> morton_vec(input_vector_num * morton_dim);
  std::vector<uint64_t> origin_input_vector(input_vector_num * input_vector_dim);
  std::vector<uint64_t> Mask_bit = Mask_Table(input_vector_dim);
  int left_shift_init = std::pow(2,Mask_bit.size()-1)* (input_vector_dim - 1);
  int left_shift, inv_morton_dim;

  for (int md = 0; md < morton_dim; md++) {

    for (int nd = 0; nd < input_vector_num*input_vector_dim; nd++) {
      origin_input_vector[nd] = ( input_vector[nd] >> init_data_shift * md);
    }

    left_shift = left_shift_init;
    for (int m = 0; m < Mask_bit.size(); m++) {
      for (int nd = 0; nd < input_vector_num*input_vector_dim; nd++) {
        origin_input_vector[nd] = (origin_input_vector[nd] |( origin_input_vector[nd] << left_shift)) & Mask_bit[m];
      }
      left_shift /= 2;
    }

    inv_morton_dim = morton_dim - 1 -md;
    for (int d = 0; d < input_vector_dim; d++) {
      for (int n = 0; n < input_vector_num; n++) {
        morton_vec[n * morton_dim + inv_morton_dim] |= (origin_input_vector[n * input_vector_dim + d] << (input_vector_dim -1 -d));
      }
    }

  }
  return morton_vec;
}

mask_bitの計算

mask_table
std::vector<uint64_t> Mask_Table(int Dim) {
  int msk_size = 0;
  if(Dim==2){
    msk_size =6;
  }
  if(Dim==3){
    msk_size =6;
  }
  if(Dim==4){
    msk_size =5;
  }
  if(Dim==5){
    msk_size =5;
  }
  if(Dim==6){
    msk_size =5;
  }
  std::vector<uint64_t> Mask_bit(msk_size);
  if (Dim == 2) {
    Mask_bit = {
        0xFFFFFFFF,  
        0xFFFF0000FFFF, 
        0xFF00FF00FF00FF, 
        0xF0F0F0F0F0F0F0F,  
        0x3333333333333333, 
        0x5555555555555555}; 
  }
  else if (Dim == 3) {
    Mask_bit = {
        0x1FFFFF,  
        0x1F00000000FFFF,  
        0x1F0000FF0000FF,  
        0x100F00F00F00F00F,  
        0x10C30C30C30C30C3,  
        0x1249249249249249};  
  }
  else if (Dim == 4) {
    Mask_bit = {
        0xFFFF,   
        0xFF000000FF, 
        0xF000F000F000F,  
        0x303030303030303, 
        0x1111111111111111};  
  }

  else if (Dim == 5) {
    Mask_bit = {
        0xFFF,
        0xF00000000FF,  
        0xF0000F0000F, 
        0xC0300C0300C03,
        0x84210842108421}; 
  }
  else if (Dim == 6) {
    Mask_bit = {
        0x3FF,              
        0x30000000000FF,    
        0x300000F00000F,    
        0x3003003003003,    
        0x41041041041041};
  }
  else {
    exit(1);
  }
  return Mask_bit;
}

Z値の計算方法の紹介ができましたので，以下，k-NNの計算を説明します．

k-NNの計算

素朴な計算によるk-NN

まず，高速でない方法(素朴な方法)によるk-NNの計算を紹介します．これは全てのトレーニングデータと全てのクエリデータとの間の距離を計算し，その後k個の近傍点を選ぶことで計算することができます．
image.png

この方法は，トレーニングデータおよびクエリデータの数が十分に少なければ高速に計算できますがデータの数が多くなると計算コストが膨大なものとなります．
(図の例では，クエリデータ1つに対してトレーニングデータが7つあり，1×7で7回距離計算を行いますが，クエリデータが100万点，トレーニングデータが100万点あった場合は100万×100万回の距離計算で計算コストは莫大なものとなります．)

Z-curveを用いたk-NNの計算

続いて，Z-curveを用いたk-NNの計算について紹介します．
Z-curveの性質として，
「Z-curveを用いてデータを多次元空間から一次元空間へと写像したとき，
多次元空間上でのデータ同士の局所的な位置関係の情報を保持したまま写像することが可能」
というものを紹介しました．この性質を用いて計算を高速化します．
高速化のお気持ちとしてはざっくりと近傍の点を選んで，その中からクエリデータPとトレーニングとの距離を計算して，最後にk近傍点を探すという方法です．
image.png

そしてこのざっくりとした近傍の点というものを計算によって決定します．(人の目には近傍の点というものは明らかですがコンピュータにとっては必ずしもそうではありません．また，図では2次元の例を示していますが，4次元，5次元となってくると人間の目でざっくりとした点を見つけることは難しくなります．)

では具体的な計算の手順を紹介しましょう．
Z-curveを用いたk-NNの計算では処理が大きく二つに分かれます．
前処理計算とクエリ処理計算の二つです．前処理計算ではトレーニングデータをZ値に変換し，Z値によってソートしておきます．そして，このソートされたトレーニングデータを本記事では，Z-curve上のトレーニングデータという表現もします．

前処理

  1. トレーニングデータについてZ値を計算する．
  2. トレーニングデータをZ値によってソートする．
    • Z値は多次元配列で与えられるので基数ソートによってソートを実行する．
    mojikyo45_640-2.gif

続いて，クエリ処理計算について紹介します．

クエリ処理

  1. クエリデータPについてZ値を計算する．

  2. クエリデータP(Z値)をソートされたトレーニングデータ(Z値)内部に配置する．

    • 前処理で計算したソートされたトレーニングデータのZ値とクエリデータのZ値を比較して，ソートされたトレーニングデータの順序に従いクエリデータの位置を決定する．これは二分探索によって高速に計算することができる．
    mojikyo45_640-2.gif

  3. クエリデータ(Z値)の前後k点のトレーニングデータを選ぶ．
    mojikyo45_640-2.gif

  4. 選んだトレーニングデータとクエリデータの元の多次元空間での距離を計算する．
    mojikyo45_640-2.gif

    • 図の水色で囲ったトレーニングデータ(2k個)とクエリデータPとの距離を求める．

  5. 計算した距離の中でk番目に小さい距離を，仮の近傍球半径Rと呼ぶ．
    mojikyo45_640-2.gif

  6. クエリデータを中心として，Rを半径とするような超球を考える．
    mojikyo45_640-2.gif

  7. この超球を含む最小の矩形を考える．この矩形の頂点の中で，最も小さい点とZ値が大きい点を始点と終点と呼ぶ．

    • クエリデータPの座標を(X,Y)とすれば始点の座標は(X-R,Y-R)，終点の座標は(X+R,Y+R)である．
    mojikyo45_640-2.gif

  8. 始点と終点のZ値を計算する．

  9. Z-curve上において始点と終点の間にある全てのトレーニングデータとクエリデータPの距離を計算する．

    • このとき選ばれたトレーニングデータは必ずクエリデータPに対する真のk近傍点を含む．

  10. 計算した距離からk近傍点を求めれば，厳密なk-NNの計算ができる．

具体的な実装については長くなるので本記事では紹介はしませんが，興味のある方は挑戦してみてください．

なぜ厳密なk-NNが計算できるか

ここでは，厳密なk-NNが計算できる理由を述べます．クエリ処理の3ステップ目で行った操作では，クエリデータと2k個のトレーニングデータの距離計算をしています．4ステップ目では，その中からk番目の距離を計算しており，この時に計算したk番目のトレーニングデータとクエリデータの距離はクエリデータの厳密なk近傍点との距離よりも大きい．よって，ステップ5の超球は必ず真のk近傍点を含むため，超球を含む矩形の中を走査することで(Z-curveは矩形内部の点を全て通るので)k近傍点を見つけることができます．

評価

評価ではk=3のときのk-NNグラフの計算をしています．クエリデータとしてトレーニングデータを用いて入力するデータセットの各データについて，最も近い3つのデータを計算します．(そのうち，1つはデータ自身であって，そのときの距離は0)
評価は，人工データを用いて計算を行います．用いるデータの条件は，データ数が100万，データの次元数は2次元から6次元とします．データの値域は[0,10000]で，データは一様乱数を用いて生成しています．
また計算にあたって用いるコア数はx86が12コア，VEが8コアで計算をしています．
(VE：ベクトルエンジン)
まず，冒頭で紹介した素朴な計算方法(brute force)との比較を見てみましょう．
この計算ではbrute force，提案手法ともににVEを用いて計算をしています．

2 3 4 5 6
brute force(VE) 631.01[sec] 648.63[sec] 630.25[sec] 618.06[sec] 630.75[sec]
提案手法(VE) 1.24[sec] 1.43[sec] 1.84[sec] 3.05[sec] 6.72[sec]

brute forceによる手法と比べて提案手法は，このデータによる計算では約100倍から600倍程度高速に計算できることが分かります．

続いて，Pythonの有名な機械学習ライブラリであるscikit-learnのk-NNと比較しましょう．
scikit-learnのk-NNにも高速化のためのオプションがあり，scikit-learnではkd-treeを使って計算コストの削減を行うことができます．
計算結果は以下です．

2 3 4 5 6
scikit-learn(x86) 3.37[sec] 5.91[sec] 13.22[sec] 21.89[sec] 44.77[sec]
提案手法(x86) 1.33[sec] 2.45[sec] 4.16[sec] 9.50[sec] 23.8[sec]
提案手法(VE) 1.24[sec] 1.43[sec] 1.84[sec] 3.05[sec] 6.72[sec]
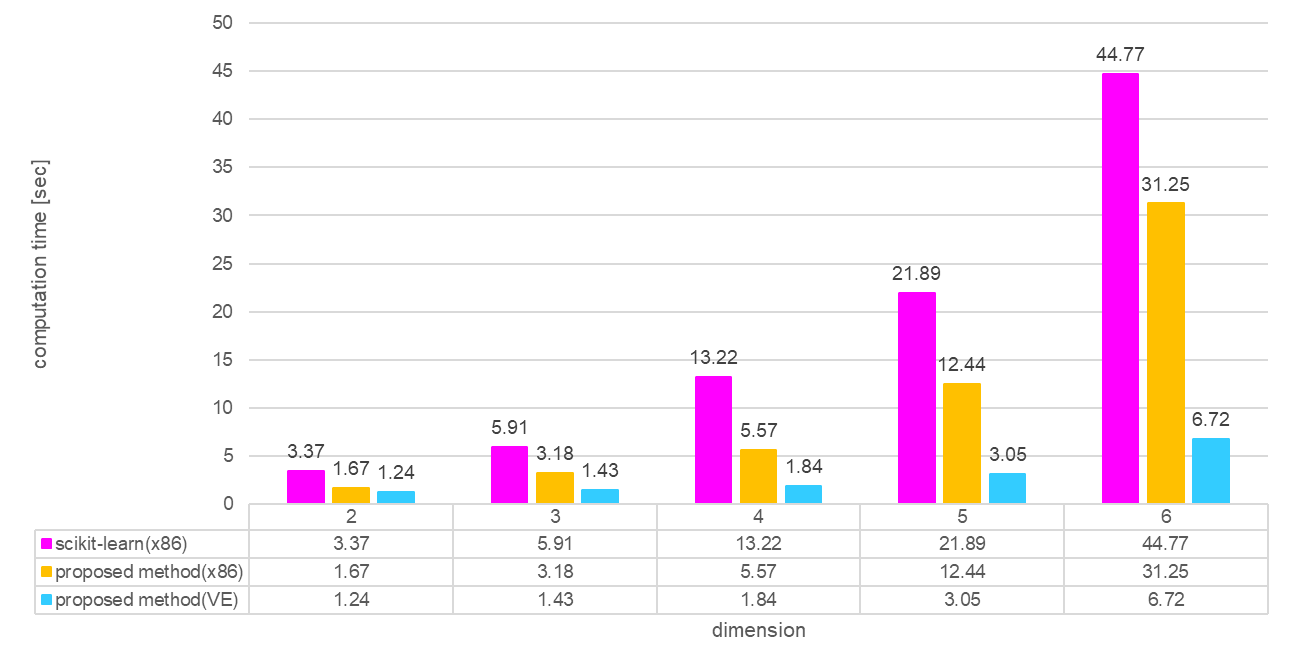
mojikyo45_640-2.gif

提案手法(x86)はscikit-learn(x86)に比べて約2倍から3倍の速度で計算を実行できています．
更に，提案手法(VE)はscikit-learn(x86)に比べて2次元のときは3 倍ほどの速さですが，次元が上がるほどに計算時間の差が大きくなり，6次元のときは7倍ほどの速さで計算ができています．
次元が上がるほどにVEが得意な計算が増えるため(ベクトル長が大きくなる)，scikit-learn比で高速化がされています．

おわりに

この記事では，Z-curveの計算とZ-curveを用いたk-NNの高速化について説明を行いました．
低次元に限りますが，Z-curveを用いたk-NNは高速に計算できることが分かってもらえたかと思います．
Z-curveによる位置情報を保持する写像は強力ですが，Z値の計算自体は複雑です(特に3次元以上)．Z値の計算法について日本語での丁寧な記述が少なかったため，この記事では読み手が計算を1ステップずつ理解することを目標して作成しました．
誤字，間違った記述等ありましたら知らせていただけると幸いです．

また，評価で載せた計算では，更に解の候補点となるトレーニングデータを減らすことで計算を速くしているのですが，内容がかなり複雑になり，話の本筋から外れるため本記事では説明を省いています．基本的なアイデアは参考文献[2]にありますので，気になる方は目を通してみてください．

参考

  1. Michael Connor, Piyush Kumar: Fast construction of k-nearest neighbor graphs for point clouds, IEEE Transac-tions on Visualization and Computer Graphics, 16:599-608, 2010.
  2. Duncan Bates: COTS embedded database solving dynamic points-of-interest, A Raima Inc. Technical Whitepaper, September, 2008.
28
19
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
28
19