##背景
先日、日本代表が念願のロシアW杯の切符を手にしました。
一つ一つの試合が非常に重要が故に、審判のレベルも非常に重要になってきます。
審判によって試合の命運が命運が分かれる場合もあります。
アジアで戦うにおいては、中東の笛と呼ばれるアウェイチームに対して不利な判定を行なっている疑惑も存在しています。
そこで今回は、審判によってホームチームとアウェイチームの判定に差があるかどうかを、簡単な統計分析を用いて調査してみたいと思います。
##データ
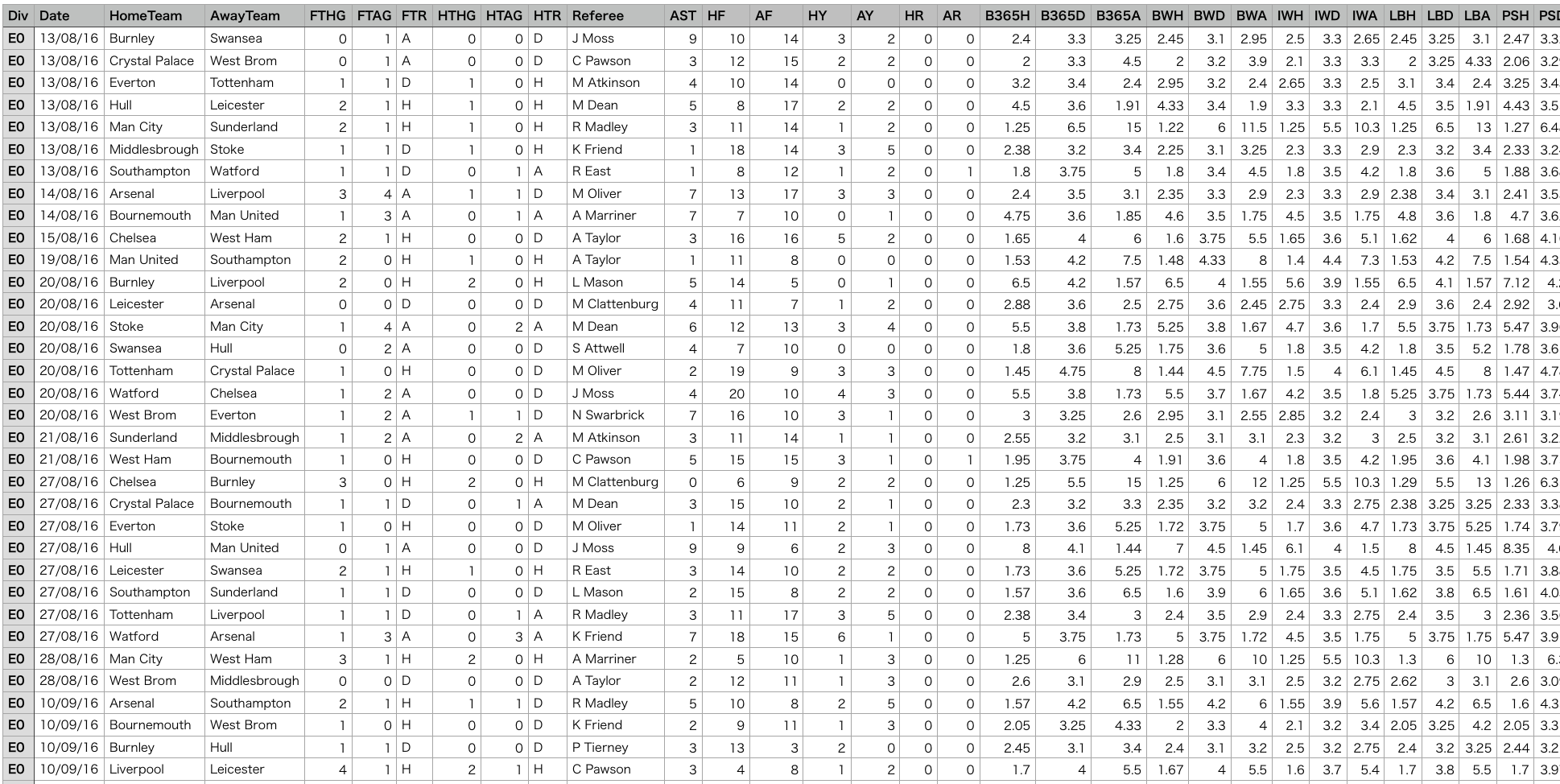
データに関しては、football-data.co.ukという海外データサイトにおいて、Premier LeagueのSeason 2016/2017の全試合データを使用します。
※本当であれば、W杯予選のデータを使用したかったのですが、ちょうどcsvにまとめられているものもありませんでしたし、スクレイピングで取得するほどの労力もかけたくありませんでした。ご了承下さい。
csvファイルは以下のようになっています。
今回は、そこから必要な情報をサマって別ファイルにまとめました。
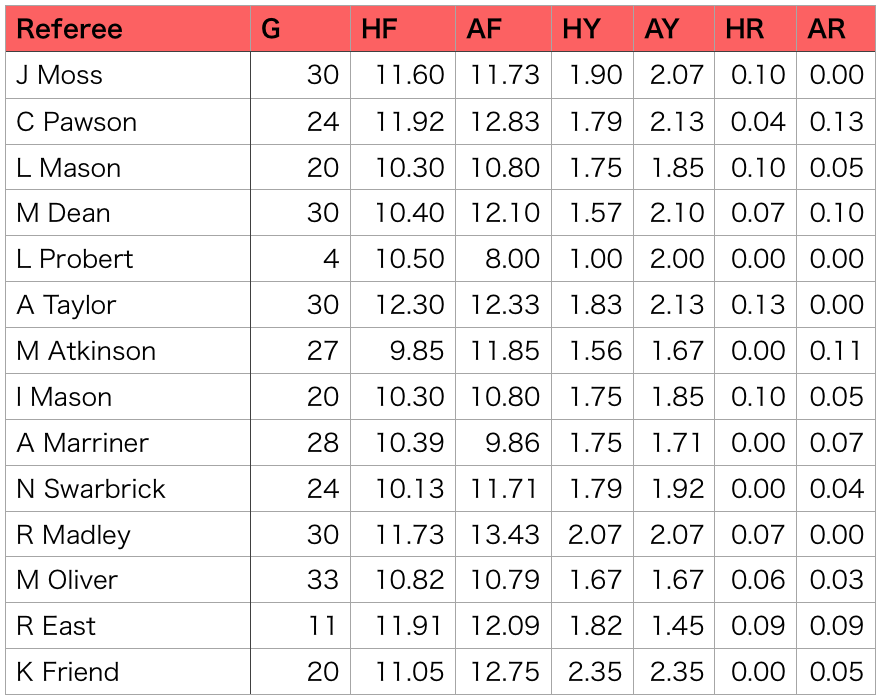
ここでの、HF、AF、HY、AY、HR、YRは各審判の試合数で割った、一試合あたりの平均値を出しています。
各項目の見方は以下の画像を参照して下さい。
##t検定
これらの項目の平均値を算出してみると以下のようになりました。
少しファール、イエローカードに関しては少しだけホーム側が少ないように思えます。
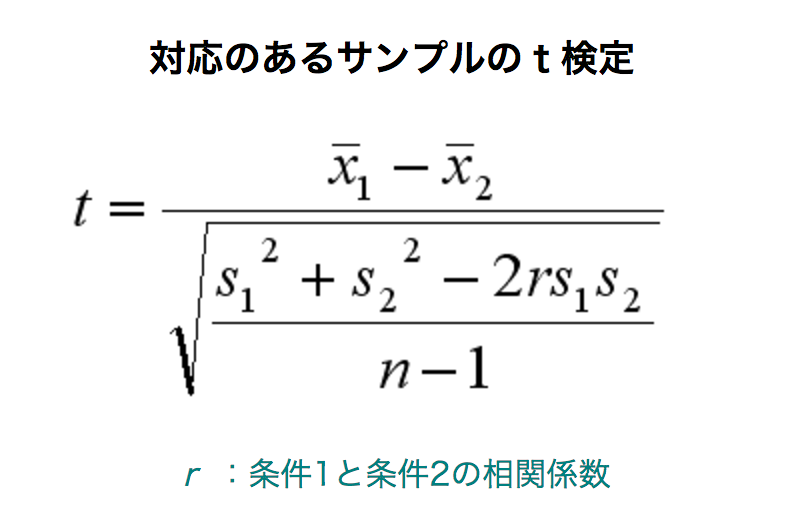
今度は対応のあるt検定を用いて、詳しく調査して見ます。
t検定とは
t検定では、2つの実験結果、2つのアンケート結果などの「平均値の差」に対して、その違いが偶然なのか（よくあるデータのバラつきなのか）、それとも何か本質的な違いがあるのか（有意水準5%または有意水準1%で差があると言えるのか）判断を下すことができる。
t検定の数式は以下のように表すことができます。
帰無仮説:ホームファール数とアウェイファール数は等しい
対立仮説：ホームファール数とアウェイファール数に差はある
とします。
では、ようやく分析に移ります。
# グラフィックス
install.packages("readxl",dep=T)
# データの読み込み
library(readxl)
# データの要約
referee_data <- read_excel("referee_data.xlsx")
#ホームデータとアウェイデータで差があるかどうかを調べる
#t検定を使用して、個人間の差を比べる
#ファール数でのt検定
t.test(referee_data$HF,referee_data$AF,paired = TRUE)
# Paired t-test
# data: referee_data$HF and referee_data$AF
# t = -1.758, df = 13, p-value = 0.1023
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -1.2549480 0.1288812
# sample estimates:
# mean of the differences
# -0.5630334
p値 p-value = 0.1023
p = 0.1023>0.05 と5%より大きいので帰無仮説は棄却できないので、
検定結果は有意でないと言えます。
つまり、ホームファール数とアウェイファール数に差はあるとは言えないという結論になります。
#イエローカード数でのt検定
t.test(referee_data$HY,referee_data$AY,paired = TRUE)
# Paired t-test
#
# data: referee_data$HY and referee_data$AY
# t = -2.0081, df = 13, p-value = 0.06588
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.3514249 0.0128401
# sample estimates:
# mean of the differences
# -0.1692924
p値 p-value = 0.06588
p = 0.06588>0.05 と5%より大きいので、
つまり、ホームイエローカード数とアウェイイエローカード数に差はあるとは言えないという結論になります。
#レッドーカード数でのt検定
t.test(referee_data$HR,referee_data$AR,paired = TRUE)
# Paired t-test
#
# data: referee_data$HR and referee_data$AR
# t = 0.14596, df = 13, p-value = 0.8862
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.03887120 0.04450406
# sample estimates:
# mean of the differences
# 0.00281643
p値 p-value = 0.8862
p = 0.8862>0.05 と5%より大きいので、
つまり、ホームレッドカード数とアウェイイレッドカード数に差はあるとは言えないという結論になります。
##考察
今回は、プレミアリーグ2016-2017シーズンにおける審判のホーム、アウェイの判定に違いがあるかどうか統計的なアプローチで分析しました。t検定を、ファール、イエローカード、レッドカードの3種類で実施したところ、全てにおいて帰無仮説は棄却されず、ホームとアウェイの判定に差はあるとは言えないという結論になりました。しかし、ファール、イエローカードに関しては有意水準5%の棄却域に近いp値をとっていました。ここでは、ファール、イエローカードに関してはホーム、アウェイ判定に偏りの傾向が見ることができました。
##まとめ
・プレミアリーグにおいて、審判のホームアウェイ判定は平等に行われている可能性が高い
・ファール、イエローカードのホームアウェイ判定には、ホーム側が有利になる傾向が見れる
「ホーム寄りの判定傾向がもう少し顕著に出てもいいかな」、と思ったんですが、
さすが欧州最高峰のリーグの審判はさすがですね。
今度は、リーグごとでの笛の吹き方の違いなどを見てみようと思います。
※データ分析系記事の投稿は初めてになりますので、至らないところがあればご指摘のほどよろしくお願いします。