Juliaで力学：ひずみテンソルを求める

\textbf{D} = \textbf{E} + \Omega = 
\begin{pmatrix}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\
\frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z}
\end{pmatrix}

前置き

Juliaでひずみテンソルを計算してみました。
専門家ではないので、間違っているところがあるかもしれません。
何か気づかれるところがありましたら、コメントお願いします。

環境

MacOS Mojave
Julia v1.0.3

相対変位テンソルとひずみテンソル

3次元空間上に与えられた2点$\textbf{r}_1$と$\textbf{r}_2$の相対変位からひずみテンソルを求める問題。

時刻 t における$\textbf{r}_1$と$\textbf{r}_2$の座標をそれぞれ

\textbf{r}_1(t)=
\begin{pmatrix}
x_1 \\
y_1 \\
z_1
\end{pmatrix}, \,
\textbf{r}_2(t)=
\begin{pmatrix}
x_2 \\
y_2 \\
z_2
\end{pmatrix}

とすると、2点間の距離$\textbf{r}(t)$は

\delta \textbf{r} = \textbf{r}_2(t) - \textbf{r}_1(t) =
\begin{pmatrix}
\delta x \\
\delta y \\
\delta z
\end{pmatrix}

また、時刻 t と時刻 t+1 の間に起こった点 $\textbf{r}_1$ の座標変化（変位）を

\textbf{u}(r_1,t) = \textbf{r}_1(t+1) - \textbf{r}_1(t)

とする。

2点間の相対変位を

\delta \textbf{u} = \textbf{u}(r_2,t) - \textbf{u}(r_1,t) =
\begin{pmatrix}
\delta u \\
\delta v \\
\delta w
\end{pmatrix}

とすると、

\delta \textbf{u} = 
\begin{pmatrix}
\delta u \\
\delta v \\
\delta w
\end{pmatrix}
= \textbf{D} \,
\begin{pmatrix}
\delta x \\
\delta y \\
\delta z
\end{pmatrix}
= \textbf{D} \, \delta \textbf{r}

と書ける。

ここで、$\textbf{D}$は相対変位テンソルであり、

\textbf{D} =
\begin{pmatrix}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\
\frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z}
\end{pmatrix}

で求められる。

さらに、$\textbf{D}$は対称テンソル$\textbf{E}$と反対称テンソル$\Omega$で

\textbf{D} = \textbf{E} + \Omega

と分解することができる。ただし、

\textbf{E} = \frac{1}{2} (\textbf{D} + \textbf{D}^T) \\
\Omega = \frac{1}{2} (\textbf{D} - \textbf{D}^T)

である。

$\textbf{E}$がひずみテンソルであり、$\Omega$は回転を表すテンソルとなっている。

参考文献：

1. 連続体の力学 (基礎物理学選書)
2. 弾性体の基礎

Juliaのコード

与えられた座標データからひずみテンソルを求める関数を実装。

$\partial$のところを$\delta$として考えて個々の要素を計算した。

function strain_tensor(r1_t1,r1_t2,r2_t1,r2_t2)
    δr = r2_t1 - r1_t1
    r1_δt = r1_t2 - r1_t1
    r2_δt = r2_t2 - r2_t1
    δu = r2_δt - r1_δt
    D = kron(δu,1/(δr)) #相対変位テンソル
    E = 1/2*(D+transpose(D)) #ひずみテンソル
    Ω = 1/2*(D-transpose(D)) #回転のテンソル
    return D,E,Ω
end

点$\textbf{r}_1$と$\textbf{r}_2$の時刻 t1 と時刻 t2 のそれぞれの座標を引数として、相対変位テンソル、ひずみテンソル、回転のテンソルを返す。

途中で使っているkronはテンソル積を求める関数。

A =
\begin{pmatrix}
x_a \\
y_a \\
z_a
\end{pmatrix}, \,
B =
\begin{pmatrix}
x_b & y_b & z_b
\end{pmatrix}

A \otimes B =
\begin{pmatrix}
x_ax_b & x_ay_b & x_az_b \\
y_ax_b & y_ay_b & y_az_b\\
z_ax_b & z_ay_b & z_az_b
\end{pmatrix}

A = [1.,2.,3.]
B = transpose([1.,4.,9.])
kron(A,B)

3×3 Array{Float64,2}:
 1.0   4.0   9.0
 2.0   8.0  18.0
 3.0  12.0  27.0

例題

時刻 t=0 での2点の座標を

\textbf{r}_1(0) = 
\begin{pmatrix}
0.0 \\
0.0 \\
0.0
\end{pmatrix}, \,
\textbf{r}_2(0) = 
\begin{pmatrix}
0.2 \\
0.2 \\
0.2
\end{pmatrix}

時刻 t=1 での2点の座標を

\textbf{r}_1(1) = 
\begin{pmatrix}
0.0 \\
0.0 \\
0.0
\end{pmatrix}, \,
\textbf{r}_2(1) = 
\begin{pmatrix}
0.3 \\
0.35 \\
0.15
\end{pmatrix}

とし、このときのひずみテンソルを求める。

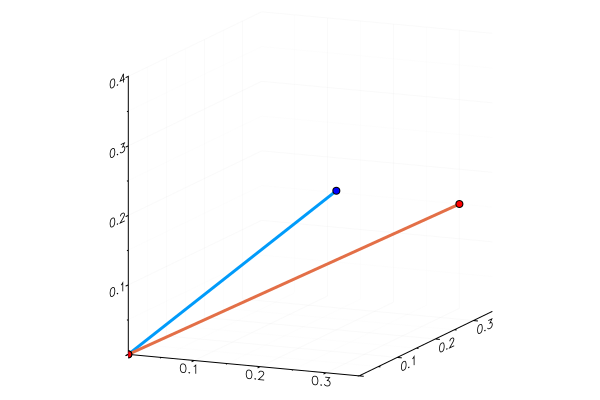
グラフを描くと

using Plots
gr()

r1_t1 = [0,0,0]
r1_t2 = [0,0,0]
r2_t1 = [0.2,0.2,0.2]
r2_t2 = [0.3,0.35,0.15]

xyz_t1 = [r1_t1 r2_t1]
xyz_t2 = [r1_t2 r2_t2]
plot(xyz_t1[1,:],xyz_t1[2,:],xyz_t1[3,:],lw=3)
plot!(xyz_t2[1,:],xyz_t2[2,:],xyz_t2[3,:],legend=:none,
    xlims=(0.0,0.35),ylims=(0.0,0.35),zlims=(0.0,0.35),lw=3)
scatter!(xyz_t1[1,:],xyz_t1[2,:],xyz_t1[3,:],color="blue")
scatter!(xyz_t2[1,:],xyz_t2[2,:],xyz_t2[3,:],color="red")

青が時刻 t=0 での2点を、赤が時刻 t=1 での2点を表す。
青から赤への変化をあらわすひずみテンソルを求めていく。

計算結果

function strain_tensor(r1_t1,r1_t2,r2_t1,r2_t2)
    δr = r2_t1 - r1_t1
    r1_δt = r1_t2 - r1_t1
    r2_δt = r2_t2 - r2_t1
    δu = r2_δt - r1_δt
    D = kron(δu,1/(δr)) #相対変位テンソル
    E = 1/2*(D+transpose(D)) #ひずみテンソル
    Ω = 1/2*(D-transpose(D)) #回転のテンソル
    return D,E,Ω
end

D,E,Ω = strain_tensor(r1_t1,r1_t2,r2_t1,r2_t2);

ひずみテンソル$\textbf{E}$の計算結果は

E

3×3 Array{Float64,2}:
 0.166667   0.208333    0.0416667
 0.208333   0.25        0.0833333
 0.0416667  0.0833333  -0.0833333

回転のテンソル$\Omega$の計算結果は

Ω

3×3 Array{Float64,2}:
  0.0        -0.0416667  0.125   
  0.0416667   0.0        0.166667
 -0.125      -0.166667   0.0 

となる。 Juliaは行列の出力が見やすくて良い感じ。

ひずみテンソル等から求められる各種パラメータも計算してみる。

using LinearAlgebra

print("体積膨張率は",round(tr(E),sigdigits=3),"\n\n")
print("x-y平面での回転は",round(Ω[2,1],sigdigits=3),"\n")
print("z-x平面での回転は",round(Ω[1,3],sigdigits=3),"\n")
print("y-z平面での回転は",round(Ω[3,2],sigdigits=3),"\n\n")
print("x-y平面でのひずみは",round(E[1,2],sigdigits=3),"\n")
print("z-x平面でのひずみは",round(E[1,3],sigdigits=3),"\n")
print("y-z平面でのひずみは",round(E[2,3],sigdigits=3),"\n")

体積膨張率は0.333

x-y平面での回転は0.0417
z-x平面での回転は0.125
y-z平面での回転は-0.167

x-y平面でのひずみは0.208
z-x平面でのひずみは0.0417
y-z平面でのひずみは0.0833

ちなみに、trは$Trace$（トレース）。Juliaの標準の関数ではないので注意。
LinearAlgebraをインポートして使う。