はじめに
これまでに{pls}のgasolineデータを使って多変量解析を実施してきた。使用したデータはガソリンの近赤外スペクトルデータとオクタン価のセットである。近赤外スペクトルは、化合物の原子間の結合モードに依存する吸収や粒子表面の反射などの物理的特性に依存した情報が含まれている。そのため、予測対象となるオクタンの含有量とは関連性の低い波長領域も含まれており、そのような関係性の低い領域の変動が予測におけるノイズとなることもある。
そこで、今回は{GA}パッケージを用いて遺伝的アルゴリズムで部分二乗回帰によるモデリングに使用する波長領域の組み合わせを最適化し、全波長のデータを使う場合よりも精度の高いモデルが得られるかざっくりと検証してみた。
遺伝的アルゴリズム
遺伝的アルゴリズムは、生物の優勢生殖を模倣した最適化アルゴリズムである。ランダムに発生した第一世代を評価し、成績が良いものに対して、交差と突然変異をランダムに加えて第二世代を生成し、再び評価する。これを繰り返すことによってより良い結果が得られる遺伝子(条件)を探索する。
今回は、gasolineデータを使用する。NIRスペクトルデータは401個の波長における吸光度が含まれているため、この401個の波長を前から順に10個のグループに分けて、それらの組み合わせを最適化することにした。第1から第9個グループは40個、第10グループには41個の波長データが含まれる。
NIR <- unclass(gasoline$NIR)
octane <- gasoline$octane
# wavelength
wl <- colnames(NIR) %>% gsub(" nm", "", .) %>% as.numeric()
# group
grs <- c(rep(1:10, each = 40), 10)
10個の波長領域の組み合わせを最適化するため、10ビットのデータ(0または1が10個)を染色体とする。イメージとしては以下のような感じ。以下の例のときには、第3, 5, 7, 8, 9グループのデータを採用するということになる。
bits <- floor(runif(10, min=0, max=2))
# [1] 0 0 1 0 1 0 1 1 1 0
次に、遺伝的アルゴリズムで最適化する上で指標となる関数を定義する。関数の中身は、採用する波長の配列を作成し、次にPLSモデルを構築している。潜在変数は10個に固定した。得られたモデルにおいて、予測平方二乗誤差(PRESS)が最小となる潜在変数でのPRESSを返す設計とした。
myFunc <- function(x) {
# select wavelength
flag <- c()
for (i in 1:10) {
if (x[i] == 1) flag <- c(flag, which(grs == i))
}
# modeling
df <- list()
df$x <- NIR[, flag]
df$y <- octane
model <<- plsr(y ~ x, data = df, ncomp = 10, validation = 'LOO')
# print(summary(model))
# evaluation
minPRESS <- which.min(model$validation$PRESS)
res <- model$validation$PRESS[minPRESS]
return(res)
}
次に、いよいよ遺伝的アルゴリズムによる最適化を実行する。今回は、10個の各グループの採否に対応する10bit(nBits)のバイナリデータ(type)が最適化をする遺伝子となる。最適化の対象を定義するfitnessには先ほど定義した関数をお決まりの形式で与える。popSizeは、1世代ごとに生成する遺伝子の数、maxiterは繰り返す世代の最大数、crossoverは交叉(遺伝子の部分構造の交換)の発生頻度、mutationは突然変異(ランダムな0と1の変換)の発生頻度を定義する。その他の引数としては、elitismという現世代の上位いくつの遺伝子をそのまま次の世代に渡すかを定義する引数があるが、今回はデフォルトの上位5%とした。
GA <- ga(type = "binary",
fitness = function(x) - myFunc(x),
nBits = 10,
popSize = 50,
maxiter = 100,
crossover = 0.8,
mutation = 0.1,
optim = TRUE)
summary(GA) # print model summary
# ── Genetic Algorithm ───────────────────
#
# GA settings:
# Type = binary
# Population size = 50
# Number of generations = 100
# Elitism = 2
# Crossover probability = 0.8
# Mutation probability = 0.1
#
# GA results:
# Iterations = 100
# Fitness function value = -2.26087
# Solution =
# x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
# [1,] 0 0 0 1 1 1 0 0 1 0
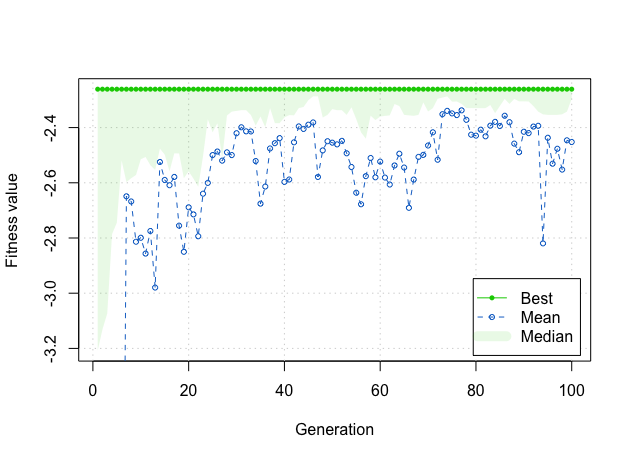
plot(GA) # visualization of learning path
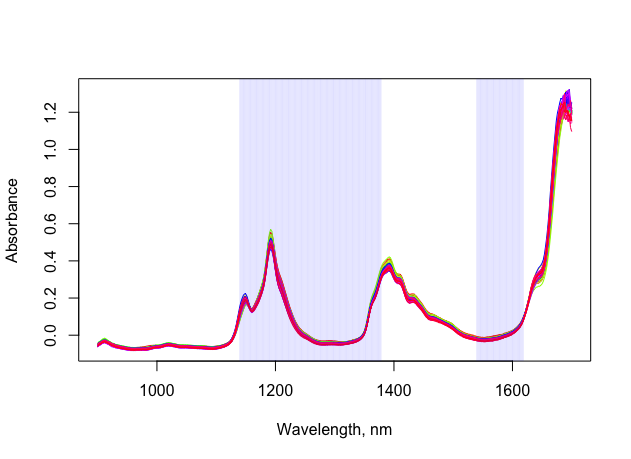
最適化の結果、第4, 5, 6, 9グループの組み合わせが最適化組み合わせとして導かれた。選択された波長領域を可視化すると以下のような図になる。
導かれた組み合わせにおけるPRESSの最小値は2.26087であった。全ての波長領域を使用して構築したモデルにおけるPRESSの最小値は2.88128であり、変数を選択することによって予測誤差を小さくできる可能性が示された。
all <- list()
all$x <- NIR
all$y <- octane
model_all <- plsr(y ~ x, data = all, ncomp = 10, validation = 'LOO')
model_all$validation$PRESS
# 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps 9 # comps 10 comps
# y 105.8417 8.723785 3.990567 3.489263 3.48936 3.158774 2.88128 3.118315 3.518667 3.573775
おわりに
今回は、遺伝的アルゴリズムを使ってNIRスペクトルデータを使った予測モデルの最適化を行なった。遺伝的アルゴリズムは再現性の確保が難しいが、局所最適解に落ちるリスクが低いといったメリットがあり、また、少しずつ進化していく過程がなんとなくかわいかったりする。他のアルゴリズムと組み合わせながらうまく使っていきたい。