はじめに
最近、統計学の復習をしているので、備忘録を兼ねて確率変数の四則演算についてまとめます。
統計学とは
統計学に関する有名な逸話としてポアンカレとパン屋の話があります。
その逸話とは、以下のような内容です。
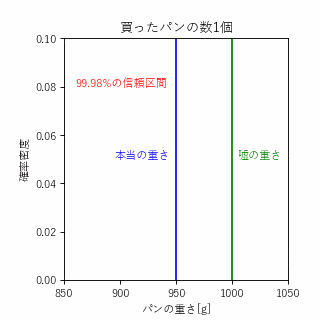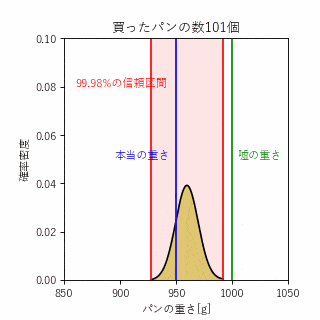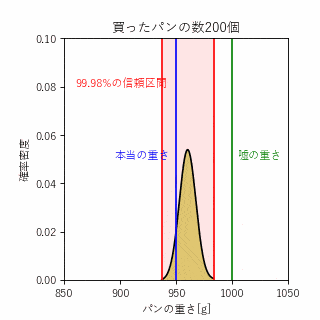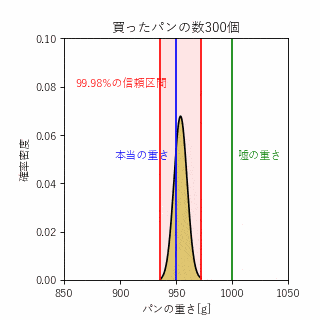
ポアンカレが馴染みのパン屋で、重量1000gのパンをよく買っていたそうですが、どうも重さをごまかされていると感じたポアンカレは買ったパンの重さを毎回計ることにしました。1年間データを蓄積したポアンカレは、これまで買ってきたパンの重さが平均950gの正規分布となっていることを訴えて、不正を見破ったそうです。
ここで、統計学の区間推定という手法を用いることで何%の確信度でパン屋が不正しているということを定量的に評価することができます。
統計学における四則演算
いきなり区間推定の説明に行く前に、統計学における四則演算の公式を理解する必要がありますので、公式の導出を行っていきます。
便宜上、以下のような記号と数式を定義します。また、簡単のためにパンの重量は整数値しか取らない離散値と仮定してしまいますが、連続値(実数)の場合は$\sum_{}$の演算を$\int$とします。
記号と数式の定義
・$X=(x_1,x_2,x_3・・・x_n):$確率変数(パンの重さが取りえる値、例えば900g,901g,902g・・・1000g,1001g,1002gなど)
・$f(x):$確率関数(パンの重さがxとなる確率、例えばf(900g)=0.005, f(1000g)=0.1など)
・$E(X)=\sum_{k}x_{k}f(x_k)=μ_X:$確率変数$X$の期待値($\sum$パンの重さ×その重さのパンの出現確率)
・$V(X)=\sum_{k}(x_k-μ_X)^2f(x_k):$確率変数$X$の分散($\sum$(パンの重さ-全体のパンの重さの平均)$^2$×その重さのパンの出現確率)
確率変数の期待値と分散の四則演算を導出する上で、下記では**互いに独立な確率変数$X$と$Y$**を仮定します。XとYが互いに独立とは$f(x_i,y_j)=f(x_i)×f(y_j)$が成り立ち、$x_i$の発生確率と$y_i$の発生確率に関係性がないということです。
➀「確率変数$X$+確率変数$Y$」の期待値
確率変数$X$に確率変数$Y$を足した確率変数$X+Y$の期待値を求めていきます。
\begin{align}
E(X+Y)&=\sum_{j,k}(x_j+y_k)f(x_j,y_k)\\
&=\sum_{j,k}x_jf(x_j,y_k)+\sum_{j,k}y_kf(x_j,y_k)\\
&=\sum_{j}x_jf(x_j)\sum_{k}f(y_k)+\sum_{k}y_kf(y_k)\sum_{j}f(x_j)\\
&=\sum_{j}x_jf(x_j)+\sum_{k}y_kf(y_k)\\
&=E(X)+E(Y)
\end{align}
3行目の式は$X$と$Y$それぞれの周辺確率(それぞれ$X$と$Y$の影響を排除した確率)と呼ばれるものになっています。最終的に確率変数$X+Y$の期待値は、$X$と$Y$それぞれの期待値を足しただけのものとなりました。引き算では符号が変わるだけです。
➁「確率変数$X$×確率変数$Y$」の期待値
確率変数$X$と確率変数$Y$をかけあわせた確率変数$X×Y$の期待値を求めていきます。$\sum_{j,k}$の意味としては、取りえる全ての$j$と$k$において値を足し合わせる全探索のようなイメージが理解しやすいと思います。
\begin{align}
E(X×Y)=&\sum_{j,k}\bigl(x_jy_kf(x_j,y_k)\bigr)\\
=&\sum_{j}x_jf(x_j)\sum_{k}y_kf(y_k)\\
=&E(X)E(Y)
\end{align}
確率変数$X×Y$の期待値は、確率変数$X$と$Y$の期待値をかけあわせただけのものになりました。割り算では$Y$の代わりに$1/Y$という確率変数を使えばよいです。
➂「確率変数$X$×定数$a$」の期待値
確率変数$X$に定数aをかけた確率変数$a×X$の期待値を求めていきます。
\begin{align}
E(a×X)&=\sum_{j}\bigl(a(x_j)f(x_j)\bigr)\\
&=ax_1f(x_1)+ax_2f(x_2)・・・\\
&=aE(X)
\end{align}
定数をかけただけの式となりました。割り算は定数$a$を$1/a$とするだけです。
➃「確率変数$X$+確率変数$Y$」の分散
確率変数$X$と確率変数$Y$を足した確率変数$X+Y$の分散を求めていきます。
便宜上、確率変数$X$の期待値は$E(X)=μ_{X}$として表します。
\begin{align}
V(X+Y)=&\sum_{j,k}\bigl(x_j+y_k-(μ_X+μ_Y)\bigr)^2f(x_j,y_k)\\
=&\sum_{j,k}\bigl(x_j^2+y_k^2+μ_X^2+μ_Y^2+2x_jy_k-2x_jμ_X-2x_jμ_Y-2y_kμ_X-2y_kμ_Y+2μ_Xμ_Y\bigr)f(x_j,y_k)\\
=&\sum_{j,k}\bigl(x_j-μ_X\bigr)^2f(x_j,y_k)+\sum_{j,k}\bigl(y_k-μ_Y\bigr)^2f(x_j,y_k)+2\sum_{j,k}\bigl(x_j-μ_X\bigr)\bigl(y_k-μ_Y\bigr)f(x_j,y_k)\\
=&\sum_{j}\bigl(x_j-μ_X\bigr)^2f(x_j)+\sum_{k}\bigl(y_k-μ_Y\bigr)^2f(y_k)+2\sum_{j}\bigl(x_j-μ_X\bigr)f(x_j)\sum_{k}\bigl(y_k-μ_Y\bigr)f(y_k)\\
=&V(X)+V(Y)
\end{align}
確率変数$X+Y$の分散は確率変数$X$と$Y$の分散を足し合わせただけの式となりました。ちなみに3行目の第3項目は$X$と$Y$の相関性を表す共分散という統計量で、$X$と$Y$が独立ではない場合は0とはならないので、分散に考慮する必要が出てきます。
➄「確率変数$X$×確率変数$Y$」の分散
確率変数$X$に確率変数$Y$をかけた確率変数$X$×$Y$の分散を求めていきます。
\begin{align}
V(X×Y)=&\sum_{j,k}\bigl(x_jy_k-μ_Xμ_Y\bigr)^2f(x_j,y_k)\\
=&\sum_{j,k}\bigl((x_jy_k)^2-2x_jy_kμ_Xμ_Y+(μ_Xμ_Y)^2\bigr)f(x_j,y_k)\\
=&\sum_{j,k}(x_jy_k)^2f(x_j,y_k)-μ_Xμ_Y\sum_{j,k}2x_jy_kf(x_j,y_k)+(μ_Xμ_Y)^2\\
=&\sum_{j,k}(x_jy_k)^2f(x_j,y_k)-2(μ_Xμ_Y)^2+(μ_Xμ_Y)^2\\
=&\sum_{j}x_j^2f(x_j)\sum_{k}y_k^2f(y_k)-(μ_Xμ_Y)^2 \\
=&E(X^2)E(Y^2)-(μ_Xμ_Y)^2\\
=&\bigl(V(X)+μ_X^2\bigr)\bigl(V(Y)+μ_Y^2\bigr)-(μ_Xμ_Y)^2 ※V(X)=\sum_{k}(x_k-μ_X)^2f(x_k)=E(X^2)-μ_X^2\\
=&V(X)V(Y)+μ_Y^2V(X)+μ_X^2V(Y)
\end{align}
確率変数$X×Y$の分散は、確率変数$X$と$Y$の期待値と分散を使って$V(X)V(Y)+μ_Y^2V(X)+μ_X^2V(Y)$となります。期待値のように単純に$V(X×Y)=V(X)V(Y)$とはならないので注意が必要です。
➅「確率変数$X$×定数$a$」の分散
確率変数$X$に定数aをかけた確率変数$a×X$の分散を求めていきます。
\begin{align}
V(a×X)=&\sum_{j}(ax_j-μ_{ax})^2f(x_j)\\
=&(ax_1-aμ_x)^2+(ax_2-aμ_x)^2+(ax_3-aμ_x)^2+・・・\\
=&a^2\sum_{j}(x_j-μ_{x})^2f(x_j)\\
=&a^2V(X)
\end{align}
確率変数を$a$倍すると分散は$a^2$倍となるので注意が必要です。