ニューラルネットのハイパーパラメータを最適化する方法について、Pythonモデルで試行錯誤しながら私なりの考えをまとめていこうと思っています。動作理解もかねているのでライブラリを使わずPythonだけで書いています。ハイパーパラメータの種類によっては層を深くしたディープニューラルネットモデルを扱うパートもあります。
使用したPythonモデルは公開しているのでアドバイスや間違いがあれば教えてください。
ハイパーパラメータとは
学習前に設定する以下のようなもので、学習で自動調整するパラメータ(重み、バイアス)とは区別しています。
- 学習率 ← Part1
- 重み初期値(±1, Xavier, Gaussian, He)← Part2
- 活性化関数(Sigmoid,Tanh, ReLU)← Part3
- 一括重み更新、逐次的重み更新、ミニバッチ処理 ← Part4
- レイヤー数、ニューロン数 ← Part5
- パラメータの更新方法(SGD、Adam、AdGard、Momentam、SMPROS、RMSProp) ← Part6
- 正規化 ← Part7
各ハイパーパラメータは一つづつPartに分けて扱っていく予定です。本Partは前置きと学習率の話ということで。
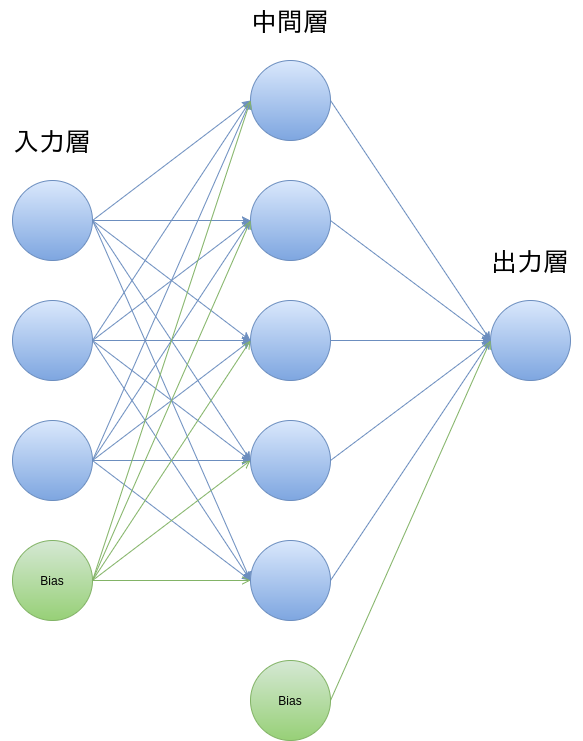
ニューラルネットの性能は入力データと上述のパイパーパラメータに依存しており、後者はそれなりの試行錯誤が必要だと思います。今回以下のようなネットワーク構成で、そのハイパーパラメータ(今回は学習率)をチューニングし学習回数や誤差が改善されるところを見ていきます。
Pythonサンプルコード
TensorFlowやCaffeなどのニューラルネットライブラリは使わず、Pythonで書いています。
動作確認したのは以下の環境ですが、Python2.7でも少しだけ動くことをみています。
- Ubuntu 14.04.5 LTS
- Python Version 3.6.0 |Anaconda 4.3.0 (64-bit)|
- numpy==1.11.3
- matplotlib==2.0.0
モデル作成時の参考書籍は下記になります。
学習とニューラルネットワーク 熊沢 逸夫(著)/森北出版

この第6章でニューラルネットワークの仕組みや導出方法が詳しく説明してあります。サンプルのCプログラムも載っていますが、Amazonの評価にもあるように書籍に記載の入力データで実行すると収束しません。ただ以下のように学習回数20万回まで増やすと17万回程度で収束しますので、この本通りに実行したのにうまくいかない方がいれば試してみてください。
# define NUM_LEARN 200000 // 学習の繰り返し回数をここで指定する
Pythonモデルで上記書籍と同様のハイパーパラメータ設定をすると収束するまで約11万回となりある程度再現できています。ここ出発点として最適化をしていきたいと思います。
本稿の対象範囲について
本稿が対象にしているのは、古典的な層の浅いニューラルネットワークや5層程度のディープニューラルネットワークのハイパーパラメータ探索で、畳み込みニューラルネットワークについての試行はしていないです(今後試したいですが)。また、ニューラルネットワークの動作や学習方法といった動作説明もしていません。こちらは上記であげた書籍や以下で詳しく載っています。特に下記書籍の誤差逆伝播法を図をつかって説明する方法はとてもわかりやすかったです。
ゼロから作るDeep Learning
――Pythonで学ぶディープラーニングの理論と実装 斎藤 康毅(著)/O'Reilly Japan

本題の学習率について
下記ハイパーパラメータを初期値=改善の余地がある値としてまずこの状態を確認していきたいと思います。
- 学習率 0.05
- 重み初期値 -1 と 1 の交互
- 活性化関数:Sigmoid
- 逐次的重み更新方法
- レイヤー、ニューロン数 入力:3/中間:5/出力:1
- パラメータ更新方法:SGD
- 正規化:なし
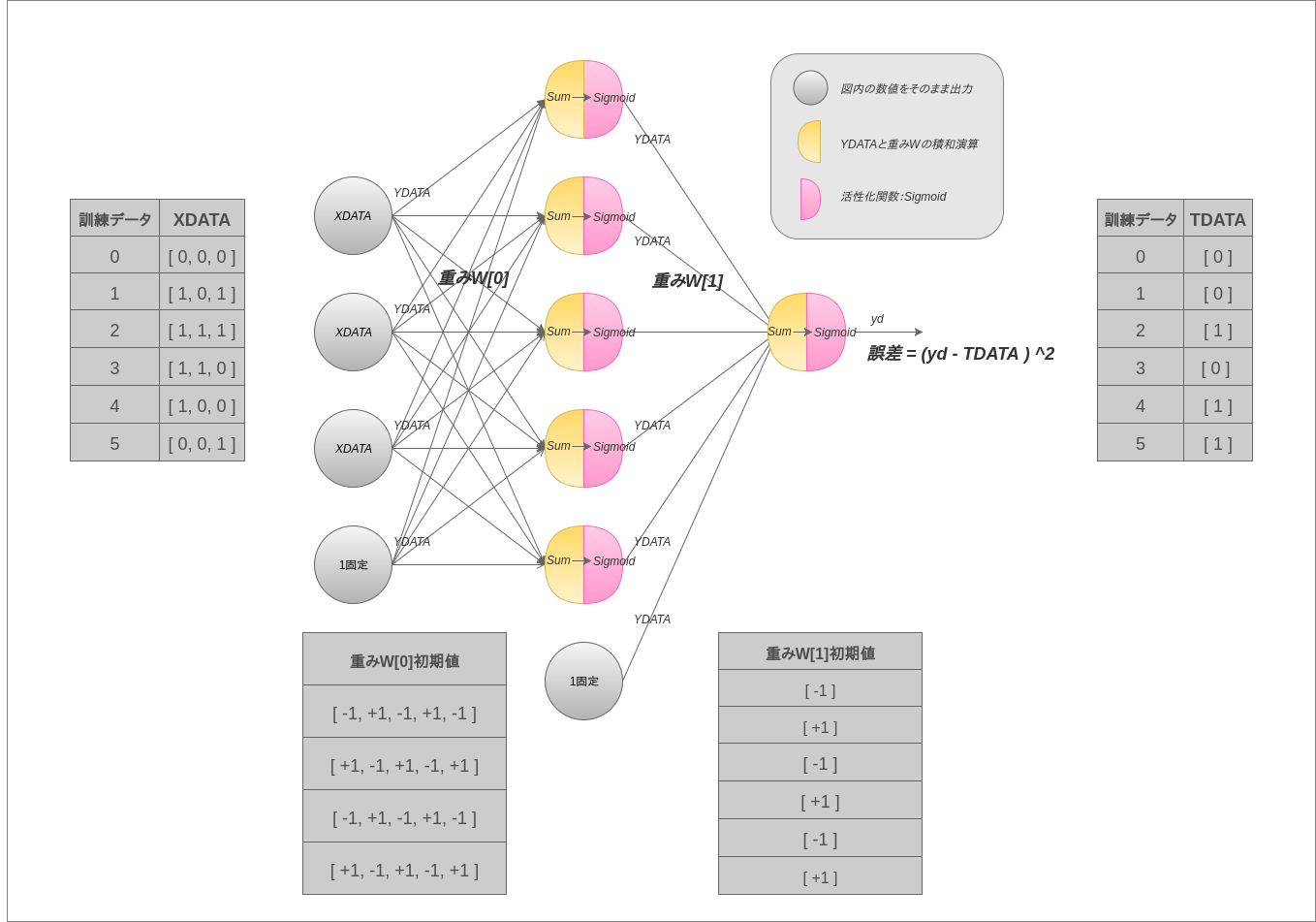
3層のネットワーク構成で、活性化関数はSigmoidをつかっています。重みの初期値は+1と-1の交互。訓練データは6つしかなく、XDATA3要素中の1の個数が偶数であればYDATAを1としています。変数(XDATA,YDATA,TDATA、W[])はソースコードと対応しているので追うときの参考にしてください。
上記の図はフィードフォワード時の図なのでハイパーパラメータのいくつかは図中に出てきませんがそのうちバックフォワードの図も書くつもりなのでそこで再度確認させてください。
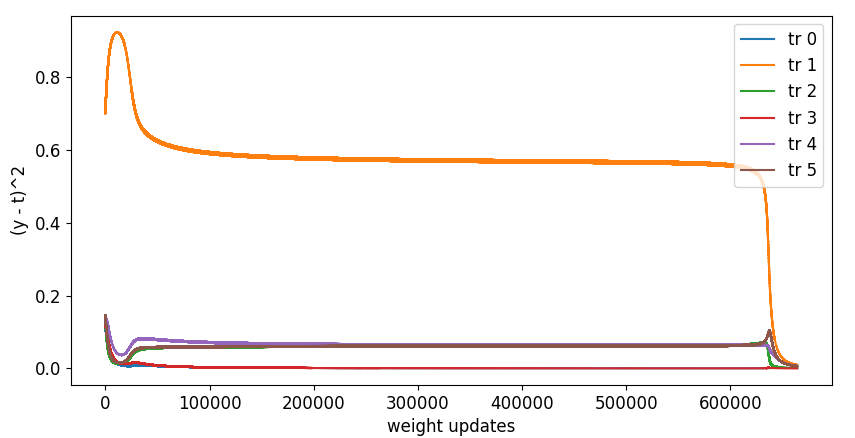
実行結果です。6つの訓練データすべてで誤差が0.01未満になるまで訓練しました。
横軸は学習回数、縦軸は上段のグラフで誤差、残りの2つはn各層の重みW[0],W[1]の推移です。
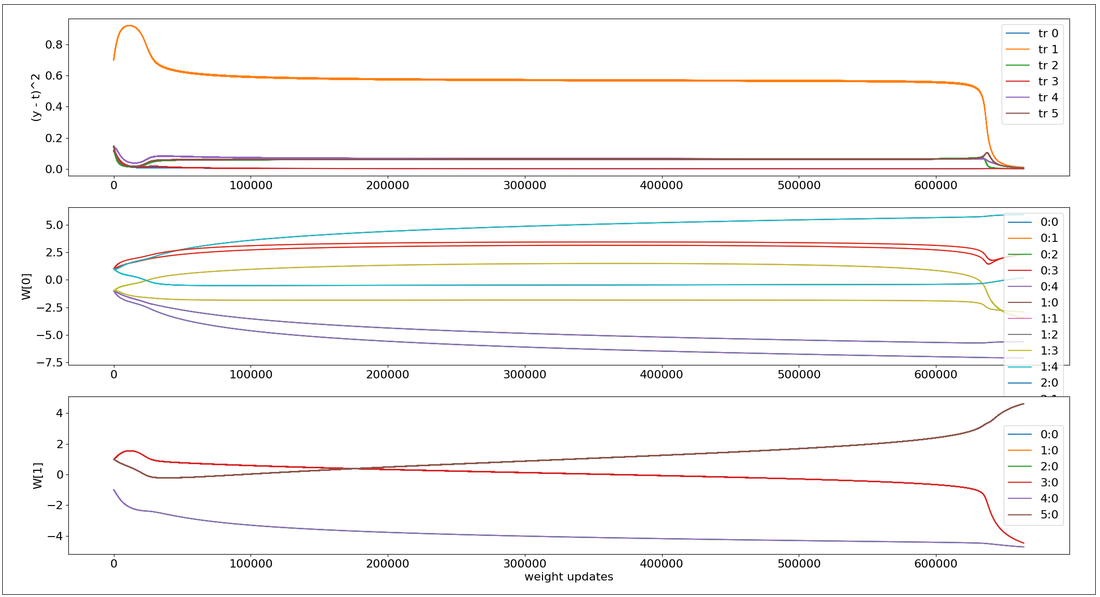
学習の最初と最後あたりは値が大きく変化していますが、それ以外のほとんどのところ(100000〜600000回あたり)は誤差がある状態にも関わらずあまり変化がなく学習がすすんでいないことを見ることができます。この期間の学習を加速するため、学習率0.05→0.5→5→50と変更してみました。ソースコードは以下を修正してください。初期値は5にしてあります。
EPSILON = 5.0 # Learning Rate
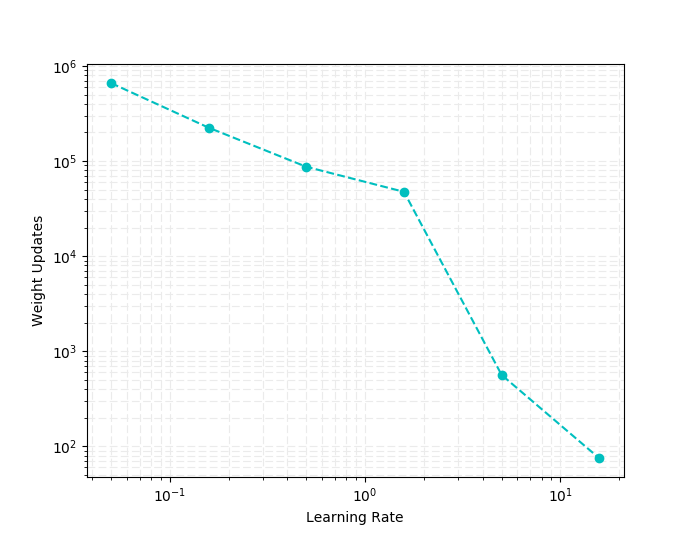
学習率を増やした時の学習回数結果を対数グラフにしました。4サンプルは少しもの足りない気がしたので、その中間値も計測しています。グラフをみると横軸:学習率に半比例して縦軸:学習回数が減っているのがわかります。ただ学習率50は大きすぎるようで、誤差が収束しなかったためグラフにのせていません。
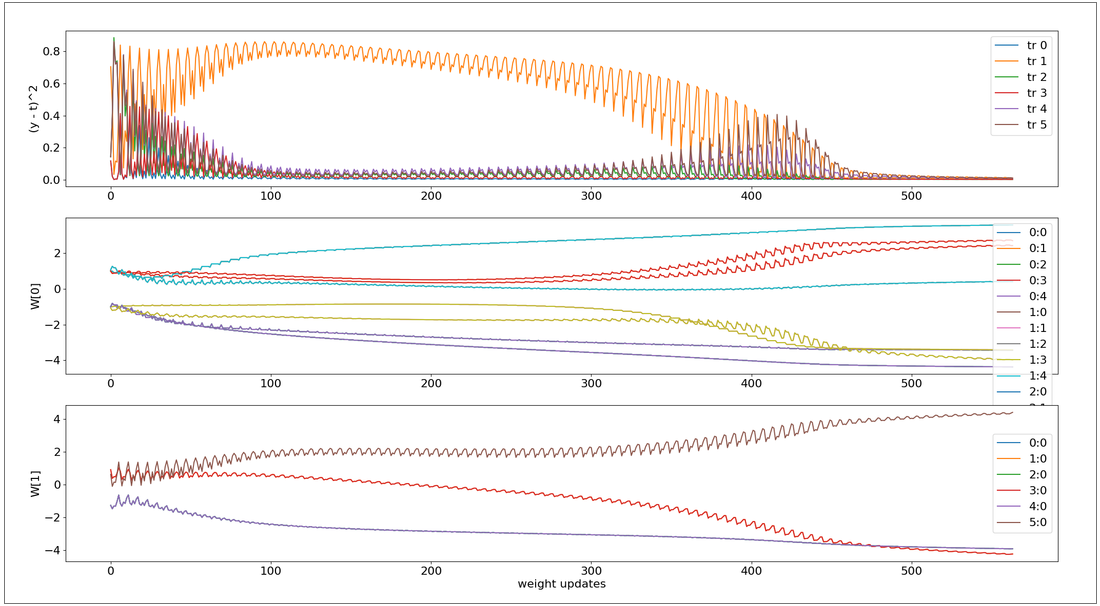
上記グラフの右から2番めにあたる学習率 5.0、学習回数 564の時の学習遷移グラフです。学習率0.05のときと比較すると学習全体を通して誤差が変化しているのがわかり、効率よく?学習しているように見えます。
まとめ
最初に試した学習率0.05では、特定のトレーニングデータ(オレンジ色のtr:1)で誤差が長期間残っていますが、最終的には収束しています。そのことから学習率を大きくしてこの勾配を早く下ったとしても最終的にはきちんと収束する可能性があり、実際大きくしたところより早く収束し学習回数も減ったといった形でしょうか。この点についてはモーメンタム※等を導入したほうがよりスマートに学習回数は減るかもしれません。※モーメンタムについてはPart7で考察したいと思います。
学習率が過大(今回は50)の場合はそもそも収束しませんが、それ以下であればどの値でも学習回数と引き換えに収束しているので、その点はハイパーパラメータの調整難易度でいうとの低い方なのかもしれません。
次回
次回取り扱うハイパーパラメータは"重みの初期値"です。中間層と出力層の間の結線は6本なので、上記グラフのW[1]には、ラインが6つあるべきところ3つしかありません。この点について重みの初期値を変更することで対応してきます。また今回のモデルより層を2つ増やし、5層にしたディープニューラルネットも扱います。