LoginSignup
7
7

More than 5 years have passed since last update.

@MENDY(MENDY)

最適追従系+積分補償器(最適サーボ)実装してみた

Last updated at Posted at 2018-06-20

はじめに

最適制御×機械学習といつつ，最適制御の内容を投稿していなかったのでします
前回は積分型最適サーボ系でしたが今回は，最適追従型＋積分補償器でサーボ系を構成します

目的

最適追従型＋積分補償器を実装

モデル

モータみたいに
一次遅れ系にします

\dot{\boldsymbol{x}}=\boldsymbol{Ax}+\boldsymbol{Bu}\\
\boldsymbol{y}=\boldsymbol{x}

\boldsymbol{A}=
\begin{bmatrix}
-1/0.54 & 0\\
0 & -1/0.54
\end{bmatrix}\\

\boldsymbol{B}=
\begin{bmatrix}
1/0.54 & 0\\
0 & 1/0.54
\end{bmatrix}

比較モデル

モデル化誤差があっても大丈夫だと証明したいので，モデル化誤差ありもかいておきます．

\acute{\boldsymbol{A}}=
\begin{bmatrix}
-1/0.54+1 & 0\\
0 & -1/0.54+1
\end{bmatrix}\\

\acute{\boldsymbol{B}}=
\begin{bmatrix}
1/0.54 & 0\\
0 & 1/0.54
\end{bmatrix}

目標信号

定値rです！定値でなくてもできますが，また今度にします

\boldsymbol{r}=
\begin{bmatrix}
5\\
3
\end{bmatrix}

定常状態

定常状態ではこのような式になるので，この式と元の状態方程式の差をとって偏差系を構成します

\boldsymbol{0=Ax_\infty+ Bu_\infty\\
r=Cx_\infty}

偏差系

ここが積分型最適サーボとは大きく異なります
とりあえずただの最適追従型を構成します

\dot{\boldsymbol{\tilde{x}}}=\boldsymbol{{A_e}\tilde{x}}+\boldsymbol{B_e\tilde{u}}\\
\boldsymbol{e}=\boldsymbol{C_e\tilde{x}}

\boldsymbol{A_e=A}\\

\boldsymbol{B_e=B}\\

\boldsymbol{C_e = -C}

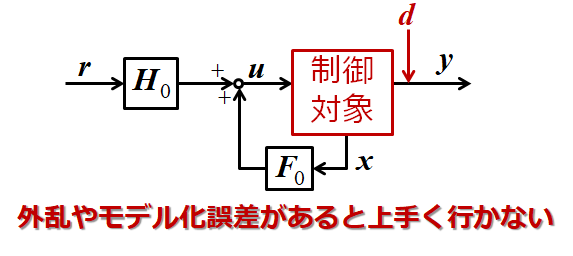
ブロック線図参照！

image.png

ここにも書いてあるようにこれだと，FF要素（フィードフォワード要素）に対して，フィードバックがないので，ただしく出力がでているのか分かりません
ただとりあえずこういう偏差系を構成すれば，最適レギュレータ理論を適用できるのでこのまま評価関数を構成します

評価関数

以下の評価関数を最小化します

\int_{0}^{\infty}\boldsymbol{e^TQe+\tilde{u}^TR\tilde{u}}dt

eは偏差を表します
チルダは最終値（目的の値）との偏差を表しています
QとRの値は適宜設定してください

最適入力

最適入力は以下のように求められます
教科書をみてみてください

\boldsymbol{u(t)=F_0x(t)+H_0r\\
F_0=-R^{-1}B^TP\\
H_0 = \begin{bmatrix}
F_0 & \boldsymbol{I}
\end{bmatrix}
\begin{bmatrix}
A & \boldsymbol{B}\\
\boldsymbol{C} & \boldsymbol{0}
\end{bmatrix}^{-1}
\begin{bmatrix}
0\\
\boldsymbol{I}
\end{bmatrix}
}

積分補償器の追加

後でシミュレーションでも確認しますが，これだとモデル化誤差がない場合はすごくうまく行きますが，あるとうまくいきません
なので，積分補償器を追加します
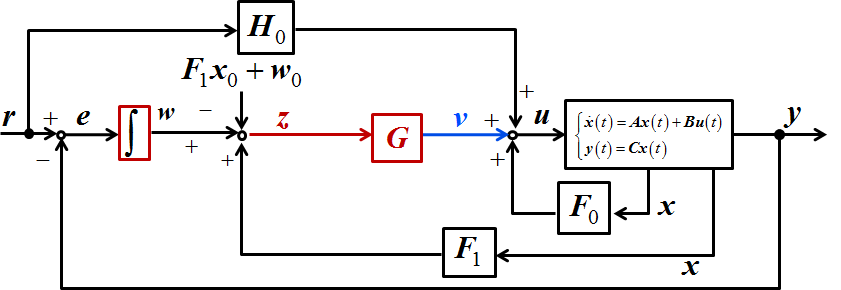
詳しい説明は論文などに任せることにしますが積分補償器を追加した，最適追従型＋積分補償器の入力は以下の式で表せます

\begin{align}
\boldsymbol{u(t)=F_0x(t)+H_0r+Gz(t)\\
z(t)=w(t)+F_1x(t)-F_1x_0-w_0}
\end{align}

ブロック線図

image.png

プログラム

Matlabで書きました
偏差系に対して、リカッチ方程式を求めています！
リカッチ方程式の解はこれでmatlabだと求められます

care

後は入力を作って、ルンゲクッタやるだけですね！！
最初のものは最適追従系のみ
2番目は積分補償器つきになります

siteki_track.m
clc
clear 
close all

%% Model
% 時定数
tau = 0.54;
tau_de = 0.54;
A = [-1/tau 0; 0 -1/tau];
B = [1/tau 0; 0 1/tau];
C = [1 0; 0 1];

% モデル化誤差ありver
A_de = [-1/tau_de+1 0; 0 -1/tau_de+1];
B_de = [1/tau_de 0; 0 1/tau_de];

%% 要件チェック
% 可制御性確認
[m_a, n_a] = size(A);%行列Aのサイズ

Ct = ctrb(A, B)
C_rank = rank(Ct)

if C_rank < m_a
    disp('Not controlable')
    quit
end

% 可観測性確認
Ob = obsv(A, C)
O_rank = rank(Ob)

if O_rank < n_a
    disp('Not observable')
    quit
end

% 入力と出力の数確認
[m_b, n_b] = size(B);
[m_c, n_c] = size(C);

if n_b < m_c
    disp('Not controlable')
    quit
end

% 今回は定値を想定（条件4は無条件にパス）
J = 0;
L = [1 0; 0 1];

[m_l, n_l] = size(L);

%% 目標値
%　x方向の速度
r_x = 5;

% y方向の速度
r_y = 3;

% 合わせたもの
r = [r_x; r_y];

%% 制御系構成
% 重みづけ
R_sub = [0.1 0.1];
R = diag(R_sub);

Q_sub = [1 1];
Q = diag(Q_sub); 

%% リカッチ方程式解法
lqr(A, B, Q, R);

[P,L,G]=care(A, B, Q, R)%連続リカッチ方程式

% 制御則導出
[m_p, n_p] = size(P);

% 必要な係数計算
F_0 = -inv(R)*(B')*P;

F_1 = C*inv(A+B*F_0);

[m_f, n_f] = size(F_0)
temp1_H_0 = [-F_0, eye(m_f)];
temp2_H_0 = inv([A, B; C, zeros(m_c, n_b)]);
temp3_H_0 =[zeros(m_c, n_b); eye(m_c)];
H_0 = temp1_H_0*temp2_H_0*temp3_H_0;

%% シミュレーション
% シミュレーション時間
k = 100;
i = 0;

% sampling 時間
dt = 0.05;

% 変数（ロボットの状態）
v_x = zeros(1, k);
v_y = zeros(1, k);
X = zeros(2, k);
U = zeros(2, k);

% 変数（ロボットの状態）モデル化誤差ありver
v_x_de = zeros(1, k);
v_y_de = zeros(1, k);
X_de = zeros(2, k);
U_de = zeros(2, k);

% グラフ用（目標値）
r_graph = zeros(2, k);
r_graph(:, 1) = r;

% 初期値
i = 0;
X_0 = [0; 0];%対象システムの状態量
X_ex(:,1) = [X_0];%拡張系の状態量
X_ex_de(:,1) = [X_0];%拡張系の状態量モデル化誤差あり

for t = 0:dt:dt*(k-1)
    i  = i + 1;
    %ルンゲクッタ
    %入力
    U(:,i)=F_0*X(:,i)+H_0*r;

    X1 = X_ex(:,i);       k1 = dt*(A*X1+B*U(:,i));
    X2 = X_ex(:,i)+k1/2;  k2 = dt*(A*X2+B*U(:,i));
    X3 = X_ex(:,i)+k1/2;  k3 = dt*(A*X3+B*U(:,i));
    X4 = X_ex(:,i)+k3;    k4 = dt*(A*X4+B*U(:,i));

    X_ex(:,i+1)=X_ex(:,i) + (k1+2*k2+2*k3+k4)/6;

    v_x(i+1) = X_ex(1,i+1);
    v_y(i+1) = X_ex(2,i+1);
    r_graph(:, i+1) = r;

    X(:,i+1) = [v_x(i+1); v_y(i+1)];    

    % ルンゲクッタ（モデル化誤差あり）
    %入力
    U_de(:,i)=F_0*X_de(:,i)+H_0*r;

    % 外乱
    d = [3; 2; 0 ;0];

    X1 = X_ex_de(:,i);       k1 = dt*(A_de*X1+B_de*U_de(:,i) );
    X2 = X_ex_de(:,i)+k1/2;  k2 = dt*(A_de*X2+B_de*U_de(:,i));
    X3 = X_ex_de(:,i)+k1/2;  k3 = dt*(A_de*X3+B_de*U_de(:,i));
    X4 = X_ex_de(:,i)+k3;    k4 = dt*(A_de*X4+B_de*U_de(:,i));

    X_ex_de(:,i+1)=X_ex_de(:,i) + (k1+2*k2+2*k3+k4)/6;

    v_x_de(i+1) = X_ex_de(1,i+1);
    v_y_de(i+1) = X_ex_de(2,i+1);
    r_graph(:, i+1) = r;

    X_de(:,i+1) = [v_x_de(i+1); v_y_de(i+1)];

end

%% Figure

% GUIのフォント
set(0, 'defaultUicontrolFontName', 'Times New Roman');
% 軸のフォント
set(0, 'defaultAxesFontName','Times New Roman');
% タイトル、注釈などのフォント
set(0, 'defaultTextFontName','Times New Roman');
% GUIのフォントサイズ
set(0, 'defaultUicontrolFontSize', 18);
% 軸のフォントサイズ
set(0, 'defaultAxesFontSize', 20);
% タイトル、注釈などのフォントサイズ89
set(0, 'defaultTextFontSize', 20);

% グラフ用時間
time=0:dt:(k)*dt;

% x方向速度時刻歴
figure('Name','v_x','NumberTitle','off')%車体速度の時刻歴
plot(time , v_x,'LineWidth',3, 'Color', [1, 0.3, 0]);
hold on
plot(time , v_x_de,'LineWidth',3, 'Color',[0, 0.3, 1]);
hold on
plot(time, r_graph(1, :),'LineWidth',3, 'Color',[0, 0, 0], 'Linestyle', ':');
hold on
grid on
hold on
box on
hold on
xlabel('time [s]','FontSize',20);
ylabel('{\it v_x} [m/s]','FontSize',20);
legend('\it v_x', '\it v_x delta', '\it r_x');

% y方向速度時刻歴
figure('Name','v_y','NumberTitle','off')%車体速度の時刻歴
plot(time , v_y,'LineWidth',3, 'Color', [1, 0.3, 0]);
hold on
plot(time , v_y_de,'LineWidth',3, 'Color',[0, 0.3, 1]);
hold on
plot(time, r_graph(2, :),'LineWidth',3, 'Color',[0, 0, 0],  'Linestyle', ':');
hold on
grid on
hold on
box on
hold on
xlabel('time [s]','FontSize',20);
ylabel('{\it v_y} [m/s]','FontSize',20);
legend('\it x_y', '\it v_y delta', '\it r_y');

これが積分補償器つき

servo_siteki_track.m
clc
clear 
close all

%% Model
% 時定数
tau = 0.54;
tau_de = 0.54;
A = [-1/tau 0; 0 -1/tau];
B = [1/tau 0; 0 1/tau];
C = [1 0; 0 1];

% モデル化誤差ありver
A_de = [-1/tau_de+1 0; 0 -1/tau_de+1];
B_de = [1/tau_de 0; 0 1/tau_de];

%% 要件チェック
% 可制御性確認
[m_a, n_a] = size(A);%行列Aのサイズ

Ct = ctrb(A, B)
C_rank = rank(Ct)

if C_rank < m_a
    disp('Not controlable')
    quit
end

% 可観測性確認
Ob = obsv(A, C)
O_rank = rank(Ob)

if O_rank < n_a
    disp('Not observable')
    quit
end

% 入力と出力の数確認
[m_b, n_b] = size(B);
[m_c, n_c] = size(C);

if n_b < m_c
    disp('Not controlable')
    quit
end

% 今回は定値を想定（条件4は無条件にパス）
J = 0;
L = [1 0; 0 1];

[m_l, n_l] = size(L);

%% 目標値
%　x方向の速度
r_x = 5;

% y方向の速度
r_y = 3;

% 合わせたもの
r = [r_x; r_y];

%% 制御系構成
%% 偏差系
% モデル化誤差なし
A_rel = [A, zeros(m_a, m_l); -C, zeros(m_c, m_l)];
B_rel = [B; zeros(m_l ,n_b)];
r_rel = [zeros(m_c, n_l); eye(m_c)];
C_rel = [-C, zeros(m_c, n_l)];

% モデル化誤差あり
A_rel_de = [A_de, zeros(m_a, m_l); -C, zeros(m_c, m_l)];
B_rel_de = [B_de; zeros(m_l ,n_b)];
r_rel_de = [zeros(m_c, n_l); eye(m_c)];
C_rel_de = [-C, zeros(m_c, n_l)];

% 重みづけ
R_sub = [0.1 0.1];
R = diag(R_sub);

Q_sub = [1 1];
Q = diag(Q_sub); 

%% リカッチ方程式解法
lqr(A, B, Q, R);

[P,L,G]=care(A, B, Q, R)%連続リカッチ方程式

% 制御則導出
[m_p, n_p] = size(P);

% 必要な係数計算
F_0 = -inv(R)*(B')*P;

F_1 = C*inv(A+B*F_0);

[m_f, n_f] = size(F_0);
temp1_H_0 = [-F_0, eye(m_f)];
temp2_H_0 = inv([A, B; C, zeros(m_c, n_b)]);
temp3_H_0 =[zeros(m_c, n_b); eye(m_c)];
H_0 = temp1_H_0*temp2_H_0*temp3_H_0;

G = -inv(R)*(F_1*B)'*[1 0;0 1];

%% シミュレーション
% シミュレーション時間
k = 200;
i = 0;

% sampling 時間
dt = 0.05;

% 変数（ロボットの状態）
v_x = zeros(1, k);
v_y = zeros(1, k);
X = zeros(2, k);
U = zeros(2, k);
V = zeros(2, k);%仮想入力

% 変数（ロボットの状態）モデル化誤差ありver
v_x_de = zeros(1, k);
v_y_de = zeros(1, k);
X_de = zeros(2, k);
U_de = zeros(2, k);

% 変数（補償器の状態）
ome_x = zeros(1, k);
ome_y = zeros(1, k);
OME = zeros(2, k);

% 変数（補償器の状態）モデル化誤差ありver
ome_x_de = zeros(1, k);
ome_y_de = zeros(1, k);
OME_de = zeros(2, k);

% グラフ用（目標値）
r_graph = zeros(2, k);
r_graph(:, 1) = r;

% 初期値
i = 0;
X_0 = [0; 0];%対象システムの状態量
W_0 = [0; 0];%補償器の状態量
X_ex(:,1) = [X_0;W_0];%拡張系の状態量
X_ex_de(:,1) = [X_0;W_0];%拡張系の状態量モデル化誤差あり

for t = 0:dt:dt*(k-1)
    i  = i + 1;    
    % 仮想入力の計算
    V(:, i) = G * (OME(:, i) + (F_1) * X(:, i) - F_1 * X_0 - W_0);

    % 入力
    U(:,i) = F_0*X(:,i) + H_0*r + V(:,i);

    % 状態更新
    X1 = X_ex(:,i);       k1 = dt*(A_rel*X1+B_rel*U(:,i) + r_rel*r);
    X2 = X_ex(:,i)+k1/2;  k2 = dt*(A_rel*X2+B_rel*U(:,i) + r_rel*r);
    X3 = X_ex(:,i)+k1/2;  k3 = dt*(A_rel*X3+B_rel*U(:,i) + r_rel*r);
    X4 = X_ex(:,i)+k3;    k4 = dt*(A_rel*X4+B_rel*U(:,i) + r_rel*r);

    X_ex(:,i+1)=X_ex(:,i) + (k1+2*k2+2*k3+k4)/6;

    v_x(i+1) = X_ex(1,i+1);
    v_y(i+1) = X_ex(2,i+1);
    ome_x(i+1) = X_ex(3,i+1);
    ome_y(i+1) = X_ex(4,i+1);
    r_graph(:, i+1) = r;

    X(:,i+1) = [v_x(i+1); v_y(i+1)];
    OME(:,i+1) = [ome_x(i+1);ome_y(i+1)];

    % ルンゲクッタ（モデル化誤差あり）
    % 仮想入力の計算
    V(:, i) = G * (OME_de(:, i) + (F_1) * X_de(:, i) - F_1 * X_0 - W_0);

    % 入力
    U_de(:,i) = F_0*X(:,i) + H_0*r + V(:,i);

    X1 = X_ex_de(:,i);       k1 = dt*(A_rel_de*X1+B_rel_de*U_de(:,i) + r_rel*r);
    X2 = X_ex_de(:,i)+k1/2;  k2 = dt*(A_rel_de*X2+B_rel_de*U_de(:,i) + r_rel*r);
    X3 = X_ex_de(:,i)+k1/2;  k3 = dt*(A_rel_de*X3+B_rel_de*U_de(:,i) + r_rel*r);
    X4 = X_ex_de(:,i)+k3;    k4 = dt*(A_rel_de*X4+B_rel_de*U_de(:,i) + r_rel*r);

    X_ex_de(:,i+1)=X_ex_de(:,i) + (k1+2*k2+2*k3+k4)/6;

    v_x_de(i+1) = X_ex_de(1,i+1);
    v_y_de(i+1) = X_ex_de(2,i+1);
    ome_x_de(i+1) = X_ex_de(3,i+1);
    ome_y_de(i+1) = X_ex_de(4,i+1);
    r_graph(:, i+1) = r;

    X_de(:,i+1) = [v_x_de(i+1); v_y_de(i+1)];
    OME_de(:,i+1) = [ome_x_de(i+1);ome_y_de(i+1)];

end

%% Figure

% GUIのフォント
set(0, 'defaultUicontrolFontName', 'Times New Roman');
% 軸のフォント
set(0, 'defaultAxesFontName','Times New Roman');
% タイトル、注釈などのフォント
set(0, 'defaultTextFontName','Times New Roman');
% GUIのフォントサイズ
set(0, 'defaultUicontrolFontSize', 18);
% 軸のフォントサイズ
set(0, 'defaultAxesFontSize', 20);
% タイトル、注釈などのフォントサイズ89
set(0, 'defaultTextFontSize', 20);

% グラフ用時間
time=0:dt:(k)*dt;

% x方向速度時刻歴
figure('Name','v_x','NumberTitle','off')%車体速度の時刻歴
plot(time , v_x,'LineWidth',3, 'Color', [1, 0.3, 0]);
hold on
plot(time , v_x_de,'LineWidth',3, 'Color',[0, 0.3, 1]);
hold on
plot(time, r_graph(1, :),'LineWidth',3, 'Color',[0, 0, 0], 'Linestyle', ':');
hold on
grid on
hold on
box on
hold on
xlabel('time [s]','FontSize',20);
ylabel('{\it v_x} [m/s]','FontSize',20);
legend('\it v_x', '\it v_x delta', '\it r_x');

% y方向速度時刻歴
figure('Name','v_y','NumberTitle','off')%車体速度の時刻歴
plot(time , v_y,'LineWidth',3, 'Color', [1, 0.3, 0]);
hold on
plot(time , v_y_de,'LineWidth',3, 'Color',[0, 0.3, 1]);
hold on
plot(time, r_graph(2, :),'LineWidth',3, 'Color',[0, 0, 0],  'Linestyle', ':');
hold on
grid on
hold on
box on
hold on
xlabel('time [s]','FontSize',20);
ylabel('{\it v_y} [m/s]','FontSize',20);
legend('\it x_y', '\it v_y delta', '\it r_y');

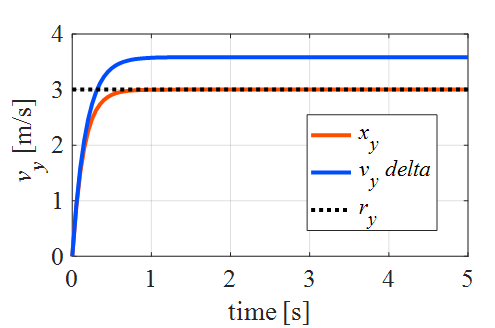
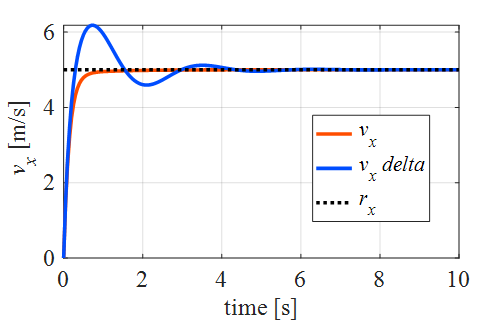
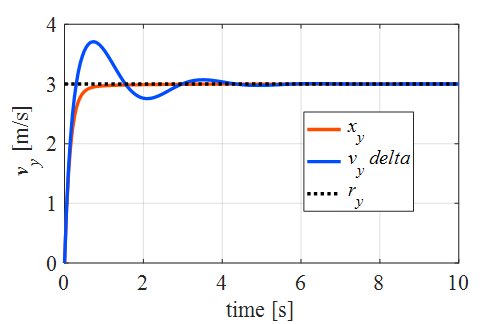
結果

こんな感じになります
まず，最適追従型のみですが，これではモデル化誤差がある場合偏差が残っていることが確認できます
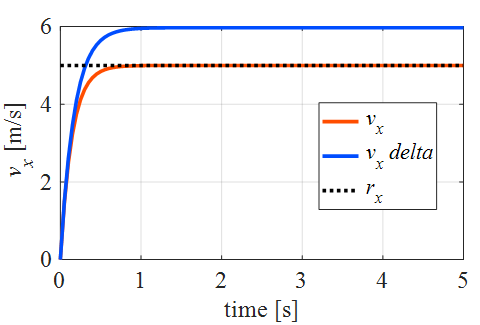
image.png

image.png

一方，最適追従型で積分補償器を追加するとうまくいくことが分かりました
モデル化誤差がない場合は積分の情報は必要ないので，積分型最適サーボ系より，
こっちの方が応答性はよさそうですね

image.png

image.png

最後に

うまくいきましたが積分型最適サーボの時と同じく定値なのでなんかなぁという感じです．
定値ではなくてもできるので，今度はそっちに挑戦します
その前にNNでも遊ぼうかと考えてます

本日のプログラム（gituhub）
https://github.com/Shunichi09/Qiita/tree/master/Control/Servo

twitter
https://twitter.com/ShunichiSekigu1

7
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
7