はじめに
初アドベントカレンダーに参加させていただきます。
Mendyです。17日目の制御工学です。
この記事は宮里義彦氏著の適応制御(コロナ社)を参考に書いています。
おしながき
- 古典制御~現代制御~これからの制御
- 適応制御とロバスト制御
- 適応制御の基礎(モデル規範型制御)
- 最後に
- プログラム
古典制御~現代制御~これからの制御
PID制御(古典制御)から始まり,状態空間モデルを用いた現代制御へと制御手法は進化をしてきました。さらに強化学習といった手法も提案をされており,さらなる進化を遂げようとしているように感じています。
そんなことにまつわる2つの経験談があります。
まず、1つ目。学部生のころ、最適制御におけるリカッチ方程式の綺麗さに感動して、なんてすごいんだってなっていました。そこまではよかったのですが、社会人の方にお会いして衝撃的な事実を聞きました。(異なる業界の場合はこのエピソードは当てはまらないかもしれません、ご理解ください)
僕「社会人って最適制御とか使うんですか?」
社会人「現代制御??いやぁPIDだよ、モーターとか動かすのはね」
僕「え?」
社会人「システム同定大変だからね、PIDで動くならPIDでいい!、もちろん不安定系は現代制御とか使うだろうけど、基本的には不安定系なら世の中に出しにくいもんね」
いやもう衝撃的でした。企業とかで最適制御って当たり前に使ってないんですね。確かに使う必要はないといえばないですけど。しかも、確かに状態空間モデルがあればすべての問題を現代制御に持って行けます。そのための手法はたくさん提案されており、状態空間モデルがあればどうにかなります。しかし、なかったら?
何もできなくなります。
そうかそうだな確かに...
ここでいろいろ調べていたら、気づいたのは
現代制御は美しすぎる制御理論である
ということです。リカッチ方程式は美しいですが、美しすぎて、状態空間モデル、つまり運動方程式でモデルが記述できなければ手も足もでません。学部生の授業でそういうこと大事なこと教えてよねってすねてました。しかもなぜか、あんまりシステム同定の授業ないという
そして2つ目。
この夏、強化学習を勉強をしていたのですが、そこでも可能性を感じてました。(ミーハーです、ごめんなさい)つまりこれはデータからもっともよい方策を決定している問題です。そしてこれなら、モデルフリーでできるし、PIDにも対抗できそうだなって少し思ってました。でもふとこんな話を聞きました。
友達「強化学習ってさ、実機でやるの大変じゃん?」
僕「え?なんで?」
友達「たくさん試したら実機壊れちゃうでしょ?」
僕「まぁ確かにそうか。でもシミュレータあればできないかな?」
友達「シミュレータ作るのにモデルを必要なんだよね、でもモデルあれば、最適化問題(制御入力を決定する問題なら最適制御)に持ってけるかもね、単純な問題であれば」
僕「・・・」
友達「しかも、強化学習って、方策を試すときに、データセット作成したときから基本的には環境のモデルが変わっちゃったら難しそうよねぇ」(これも個人的な見解があると思います、僕自身そこまで強化学習に詳しくないのですみません)
僕「・・・(またモデルの問題か・・・)」
つまり、まとめるとこうです
- 最適制御
モデルがないと何もできない
モデルがあればこっちのもの、美しい理論で非線形だろうと時変だろうとなんとかなる
- 強化学習
たくさん試して得た結果から最もよいものを学習する
環境のモデルがなくてもできる
実際にこの手法を使う場合はシミュレータを作成するのにモデルが必要になることがある、実機が壊れてしまうため
環境のモデルが時変等になってると、学習させるの困難
(上記の問題は行動決定における部分については有効かもしれません、今回はあくまでも制御入力を決定する問題ということです)
- PID
基本的にモデルフリー
偏差をフィードバックするという単純明快な手法
複雑なものは制御できないけど、単純だし産業界は基本これ
結局PIDには勝てないのかって思ってました。機械学習とかとも関係するし、システム同定を学んでみるかと思ってた矢先
モデルを作成しながら制御を行う究極の制御手法が存在する
という話を聞きました。
これしかない、と思って勉強を始めました。
(結局はまぁいろいろ前提はあるし、パラメトリックに表現される不確定要素へのアプローチなので完全にモデルフリーってわけではないですが)
適応制御とロバスト制御
上記で述べた現代制御の欠点を補うアプローチとしては大きく分けて2つあります。
- モデルがおおよそあっていれば、おおよその性能を発揮するように設計する
- 制御しながらモデルを適応的に獲得しにいくように設計する
の2点です。
お分かりだとは思いますが、上がロバスト制御、下が適応制御です。
いわゆるスライディングモード制御や、H∞制御に代表されるロバスト制御は、ある程度がモデルが間違っていても、期待された性能は発揮できるという設計指針になります。H∞とかまさにそうですね。これはこれで非常に有効です。例えば、どんな周波数帯域の外乱がくるか分からない場合、H∞ノルムを抑えにいくことで全体域でうまく抑制することが可能になります。ですので、今後そちらの方も勉強していこうと考えています。
ですが、今回は”適応”という言葉に惹かれたこともあり、調べたらちょうど本があったこともあり(適応制御についての本とかサイトとかほとんどない気がするんですが・・・)、この記事では適応制御を紹介させていただこうと思います。
適応制御の基礎(モデル規範型制御手法)
では、前置きが長くなりましたが適応制御の基礎について説明していきます。
適応制御は
- FB制御に代表される通常のフィードバック
- 制御パラメータを更新するフィードバック
の2つのフィードバックを持ちます。
これによって、モデルを適応的に習得しながら、制御を行うことが可能になります。
ブロック線図っぽく書くと
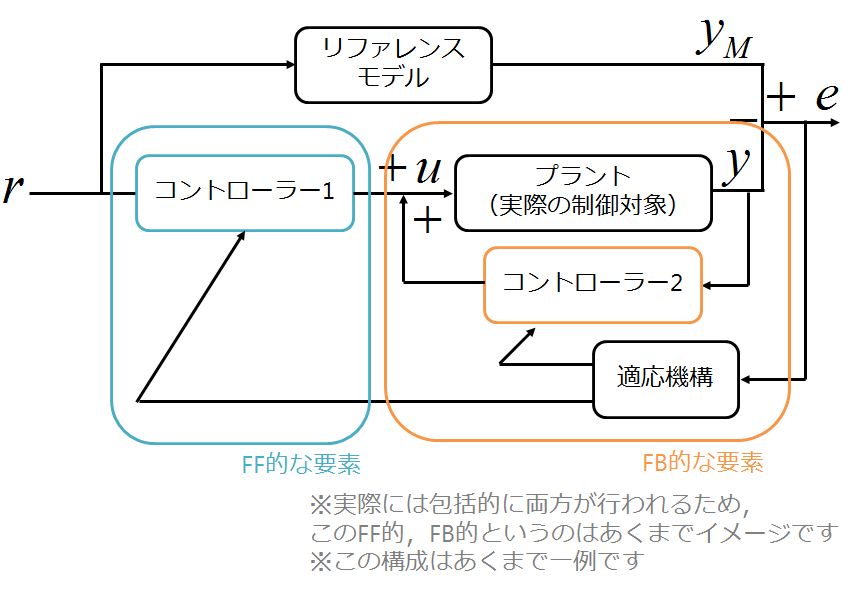
このようになります。
ここで注意点ですが、この構成はあくまで一例ということです、ほかにも提案がされています。
ちなみに通常の下記で表されるFB制御が適応制御と異なるのは

パラメータを更新するようなフィードバックが存在しないこと
です。
またゲインスケジューリングのような制御手法が適応制御と異なるのは、
制御パラメータの更新はFF的で事前に決定している
ということです。適応制御はフィードバックを用いて制御パラメータを更新していきますのでそこが異なります。
以上がおおまかな適応制御の考え方になります。
次に、具体的な設計へ入っていきますが、具体的な制御系設計で用いるのはモデル規範型適応制御(MRAC)という手法になります。
モデル規範型適応制御(MRAC)は、制御系の理想出力をモデルで与えて、それに対して追従させる手法になります。
ブロック線図的に書くと以下のようになります。

ここで$G_M$が与える理想モデル、$C_1, C_2$がコントローラー、$P$がプラントになります。また、$r$は参照入力、$u$は制御入力、$y_M$は理想出力、$y$が制御出力、$e$は偏差になります。
問題設定
今回、制御対象にするのは1次遅れ系で
y(t)=\frac{b}{s+a}u(t) \\
\dot{y}(t) + ay(t) = bu(t)
で
同じく理想モデル(以下規範モデルと呼びます)
y_M(t)=\frac{b_M}{s+a_M}u(t) \\
\dot{y_M}(t) + a_My(t) = b_Mu(t)
と設定することにします。
すると目標は偏差$e$が0になることなので
e(t) = y_M(t) - y(t)
が0になれば良いことになります。
ここで制御入力を
u(t) = \theta_1(t)r(t) + \theta_2(t)y(t)
と定めます。この決め方は、ここでは限定的に決めてますが、一般的な形に拡張することもできます。
MIT方式
具体的に設計を行います。MIT方式は偏差の2乗の勾配に向かってパラメータを変化させます
つまり、最小化させたいのは
J = \frac{1}{2}\gamma e^2 \\
ですので、これをパラメータ、$\theta_1, \theta_2$によって微分します。
\dot{\theta_1}(t) = -\frac{1}{2}g_1e(t)\frac{\partial e}{\partial \theta_1} \\
\dot{\theta_2}(t) = -\frac{1}{2}g_1e(t)\frac{\partial e}{\partial \theta_2}
のようにパラメータをその時刻ごとに変化させればよいことになります。
ちなみに$e$は以下式のように表せますので
\dot{e} + a_Me(t) = b_Mr(t) + (a-a_M)y(t) - bu(t)
さらに
\tilde {\theta_1} \equiv \frac{b_M}{b}-\theta_1 \\
\tilde {\theta_2} \equiv \frac{a - a_M}{b}-\theta_2
として
せっせと微分だの、変換だのしていくと
$\tilde {\theta_1}(t), \tilde {\theta_2}(t) \simeq 0$という仮定の下で
\dot{\theta_1}(t) = \alpha_1(\frac{1}{s+a_M}r(t))e(t)\\
\dot{\theta_2}(t) = \alpha_2(\frac{1}{s+a_M}y(t))e(t)
これでつねに偏差$e$の2乗の勾配へパラメータが変化することになります。
しかし問題点があります。
高い周波数の入力信号(sin波の周期が短いもの等)があると、毎回激しく入力が変わることになり、遅れが出てしまい、発散または、エラーが収束しないというものです。
いずれにせよ、MIT方式によるパラメータの更新式は求めることができました。
リアプノフ方式
次にリアプノフ関数を用いてパラメータの更新式を求めてみます。
MIT方式と同様に
\tilde {\theta_1} \equiv \frac{b_M}{b}-\theta_1 \\
\tilde {\theta_2} \equiv \frac{a - a_M}{b}-\theta_2
として、リアプノフ関数を
V(e, \theta) = \frac{1}{2}e(t)^2 + \frac{b}{2}(\frac{\tilde{\theta_1}(t)^2}{g_1} + \frac{\tilde{\theta_2}(t)^2}{g_2})
とします。このリアプノフを用いた場合は、いつもポイントになるのがこの関数の作成方法です。
このリアプノフ関数を見つけることができれば、時間微分をすることで安定入力(この場合は偏差が0になる入力)が求まります。
その関数を見つければ論文になるケースもあるようなぐらいハンドメイドな気がしていますし、非線形系は通常の安定解析が使えないので、このやり方を用いることが多いです。モデル予測制御なども含めてです。
今回は、パラメータの2乗と誤差の2乗の和ですので、いつもの形のような気がします。
話をもどします。
上記の式を時間微分すると、微分した結果が負になるための条件が
r(t)e(t)+\frac{\dot{\tilde{\theta_1}}}{g_1} = 0 \\
y(t)e(t)+\frac{\dot{\tilde{\theta_2}}}{g_2} = 0
になりますので、
パラメータの更新則を
\dot{\theta_1}(t) = \alpha_1 r(t)e(t)\\
\dot{\theta_2}(t) = \alpha_2 y(t)e(t)
にすればよいです!
リアプノフ関数の時間微分が負になることで、偏差$e$が0になることを確実に証明するためには、Barbalatの補題を使う必要がありますが、$L_2$ノルム等の話も必要になるのでそこは割愛します。また、さらにいうと、ここでは、偏差$e$が収束することの証明を行い、それに対応する入力の更新則を求めているだけで、システムの内部状態や、パラメータ誤差が0に収束することは証明できていませんので、そこは注意点です。
詳しい証明やそのほかの適応制御については、ぜひこの本を参考にお願いします。
数値解析
では実際に手法を適用してみます。
解析の条件を以下のように設定します。
\begin{align}
&r = \sin(t) \\
&a = -0.5\\
&b = 0.5\\
&a_M = 1\\
&b_M = 1\\
\end{align}
また更新則におけるパラメータを
\alpha_1 = 5\\
\alpha_2 = 5\\
とします。
プログラムは、最後に添付しました。
https://github.com/Shunichi09/adaptive_control にもあげてますが、ポイントは、なんとなくですが、パラメータの更新用にもループが回っているような気持ちのイメージです。
普通なら、入力が決定して、状態が更新されて、といきますが、その時にパラメータも更新します。
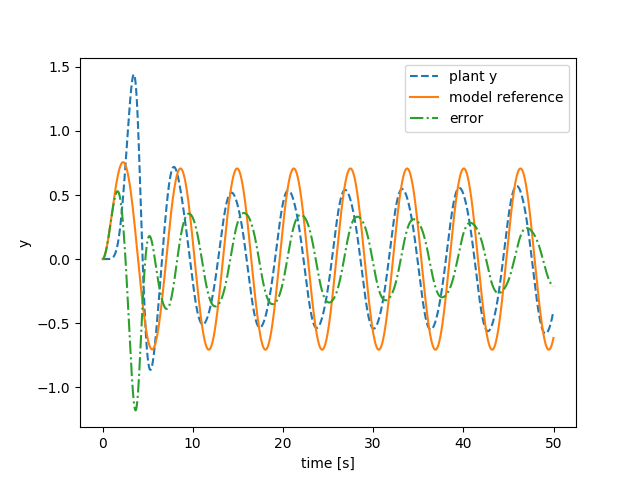
MIT方式
うまくいっていない様子が分かります。
エラーが収束していません。
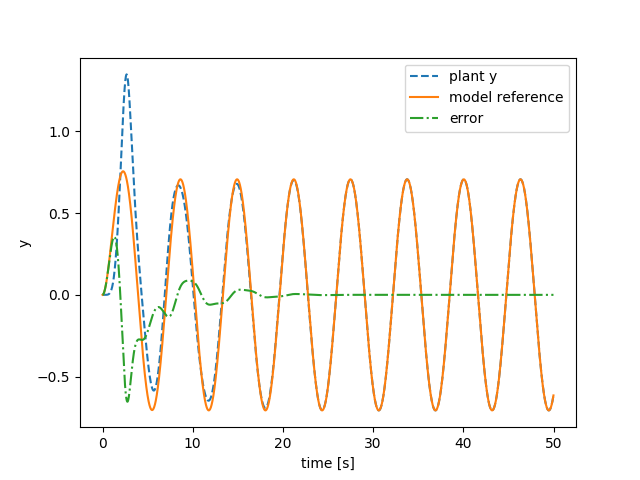
リアプノフ方式
うまくいっていますね。
エラーは早い段階で収束しています。
最後に
本記事では、制御工学アドベントカレンダー17日目として、適応制御を紹介させていただきました。
内容としては、そこまで難しいものではないとは思いますが、読んでいただいた方が少しでも興味を持っていただけたら嬉しいです。
今の世の中は時代は強化学習だの、やれ機械学習だの、たくさんライブラリが提案されて、少しでもプログラムが書ければ何かよくわかんないけど上手く行って、しかしそれを使うことできる世の中です。しかし、特に直接的にハードウェアに関わってくる部分では、安全性から、何でその結果が出たのか見えるAIつまり、Visualize AIが求められているのも確かで、制御工学分野(いわゆる機械っぽい動きをさせる)と、強化学習や機械学習(いわゆる人っぽい動きをさせる)を融合させることができれば、面白いのではないかと思っています。(あくまでイメージですが...)強化学習ももともとは、ベルマン方程式からですので、最適制御の考え方が根っこにはありますし。なにはともあれ!適応制御の基礎の紹介でした!
尚、この本のプログラムをhttps://github.com/Shunichi09/adaptive_control にあげていこうと考えています。
今はまだ第二章までですが、今後増やしていく予定です。興味がある方はぜひ一度みてください。
プログラム
MIT 方式
import numpy as np
import matplotlib.pyplot as plt
import math
class FirstOrderSystem():
"""FirstOrderSystem
Attributes
-----------
state : float
system state, this system should have one input - one output
a : float
parameter of the system
b : float
parameter of the system
history_state : list
time history of state
"""
def __init__(self, a, b, init_state=0.0):
"""
Parameters
-----------
a : float
parameter of the system
b : float
parameter of the system
init_state : float, optional
initial state of system default is 0.0
"""
self.state = init_state
self.a = a
self.b = b
self.history_state = [init_state]
def update_state(self, u, dt=0.01):
"""
Parameters
------------
u : float
input of system in some cases this means the reference
dt : float in seconds, optional
sampling time of simulation, default is 0.01 [s]
"""
# solve Runge-Kutta
k0 = dt * self._func(self.state, u)
k1 = dt * self._func(self.state + k0/2.0, u)
k2 = dt * self._func(self.state + k1/2.0, u)
k3 = dt * self._func(self.state + k2, u)
self.state += (k0 + 2 * k1 + 2 * k2 + k3) / 6.0
# save
self.history_state.append(self.state)
def _func(self, y, u):
"""
Parameters
------------
y : float
state of system
u : float
input of system in some cases this means the reference
"""
y_dot = -self.a * y + self.b * u
return y_dot
class BasicMRAC():
"""BasicMRAC
Attributes
-----------
input : float
system state, this system should have one input - one output
a : float
parameter of reference model
alpha_1 : float
parameter of the controller
alpha_2 : float
parameter of the controller
theta_1 : float
state of the controller
theta_2 : float
state of the controller
history_input : list
time history of input
"""
def __init__(self, a, alpha_1, alpha_2, init_theta_1=0.0, init_theta_2=0.0, init_input=0.0):
"""
Parameters
-----------
a : float
parameter of reference model
alpha_1 : float
parameter of the controller
alpha_2 : float
parameter of the controller
theta_1 : float, optional
state of the controller default is 0.0
theta_2 : float, optional
state of the controller default is 0.0
init_input : float, optional
initial input of controller default is 0.0
"""
self.input = init_input
# parameters
self.a = a
self.alpha_1 = alpha_1
self.alpha_2 = alpha_2
# states
self.theta_1 = init_theta_1
self.theta_2 = init_theta_2
# to slove the differential equation
self.u_1 = 0.0
self.u_2 = 0.0
self.history_input = [init_input]
def update_input(self, e, r, y, dt=0.01):
"""calculating the input
Parameters
------------
e : float
error value of system
r : float
reference value
y : float
output the model value
dt : float in seconds, optional
sampling time of simulation, default is 0.01 [s]
"""
# for theta 1, theta 1 dot, theta 2, theta 2 dot
k0 = [0.0 for _ in range(4)]
k1 = [0.0 for _ in range(4)]
k2 = [0.0 for _ in range(4)]
k3 = [0.0 for _ in range(4)]
functions = [self._func_theta_1, self._func_u_1, self._func_theta_2, self._func_u_2]
# solve Runge-Kutta
for i, func in enumerate(functions):
k0[i] = dt * func(self.theta_1, self.u_1, self.theta_2, self.u_2, e, r, y)
for i, func in enumerate(functions):
k1[i] = dt * func(self.theta_1 + k0[0]/2.0, self.u_1 + k0[1]/2.0,
self.theta_2 + k0[2]/2.0, self.u_2 + k0[3]/2.0, e, r, y)
for i, func in enumerate(functions):
k2[i] = dt * func(self.theta_1 + k1[0]/2.0, self.u_1 + k1[1]/2.0,
self.theta_2 + k1[2]/2.0, self.u_2 + k1[3]/2.0, e, r, y)
for i, func in enumerate(functions):
k3[i] = dt * func(self.theta_1 + k2[0], self.u_1 + k2[1],
self.theta_2 + k2[2], self.u_2 + k2[3], e, r, y)
self.theta_1 += (k0[0] + 2 * k1[0] + 2 * k2[0] + k3[0]) / 6.0
self.u_1 += (k0[1] + 2 * k1[1] + 2 * k2[1] + k3[1]) / 6.0
self.theta_2 += (k0[2] + 2 * k1[2] + 2 * k2[2] + k3[2]) / 6.0
self.u_2 += (k0[3] + 2 * k1[3] + 2 * k2[3] + k3[3]) / 6.0
# calc input
self.input = self.theta_1 * r + self.theta_2 * y
# save
self.history_input.append(self.input)
def _func_theta_1(self, theta_1, u_1, theta_2, u_2, e, r, y):
"""
Parameters
------------
theta_1 : float
state of the controller
u_1 : float
dummy state of the controller
theta_2 : float
state of the controller
u_2 : float
dummy state of the controller
e : float
error value of system
r : float
reference value
y : float
output the model value
"""
y_dot = u_1
return y_dot
def _func_u_1(self, theta_1, u_1, theta_2, u_2, e, r, y):
"""
Parameters
------------
theta_1 : float
state of the controller
u_1 : float
dummy state of the controller
theta_2 : float
state of the controller
u_2 : float
dummy state of the controller
e : float
error value of system
r : float
reference value
y : float
output the model value
"""
y_dot = -self.a * u_1 + self.alpha_1 * r * e
return y_dot
def _func_theta_2(self, theta_1, u_1, theta_2, u_2, e, r, y):
"""
Parameters
------------
theta_1 : float
state of the controller
u_1 : float
dummy state of the controller
theta_2 : float
state of the controller
u_2 : float
dummy state of the controller
e : float
error value of system
r : float
reference value
y : float
output the model value
"""
y_dot = u_2
return y_dot
def _func_u_2(self, theta_1, u_1, theta_2, u_2, e, r, y):
"""
Parameters
------------
theta_1 : float
state of the controller
u_1 : float
dummy state of the controller
theta_2 : float
state of the controller
u_2 : float
dummy state of the controller
e : float
error value of system
r : float
reference value
y : float
output the model value
"""
y_dot = -self.a * u_2 + self.alpha_2 * y * e
return y_dot
def main():
# control plant
a = -0.5
b = 0.5
plant = FirstOrderSystem(a, b)
# reference model
a = 1.
b = 1.
reference_model = FirstOrderSystem(a, b)
# controller
a = reference_model.a
alpha_1 = 5.
alpha_2 = 5.
controller = BasicMRAC(a, alpha_1, alpha_2)
simulation_time = 50 # in second
dt = 0.01
simulation_iterations = int(simulation_time / dt) # dt is 0.01
history_error = [0.0]
history_r = [0.0]
for i in range(1, simulation_iterations): # skip the first
# reference input
r = math.sin(dt * i)
# update reference
reference_model.update_state(r, dt=dt)
# update plant
plant.update_state(controller.input, dt=dt)
# calc error
e = reference_model.state - plant.state
y = plant.state
history_error.append(e)
history_r.append(r)
# make the gradient
controller.update_input(e, r, y, dt=dt)
# fig
plt.plot(np.arange(simulation_iterations)*dt, plant.history_state, label="plant y", linestyle="dashed")
plt.plot(np.arange(simulation_iterations)*dt, reference_model.history_state, label="model reference")
plt.plot(np.arange(simulation_iterations)*dt, history_error, label="error", linestyle="dashdot")
# plt.plot(range(simulation_iterations), history_r, label="error")
plt.xlabel("time [s]")
plt.ylabel("y")
plt.legend()
plt.show()
# input
# plt.plot(np.arange(simulation_iterations)*dt, controller.history_input)
# plt.show()
if __name__ == "__main__":
main()
リアプノフ方式
import numpy as np
import matplotlib.pyplot as plt
import math
class FirstOrderSystem():
"""FirstOrderSystem
Attributes
-----------
state : float
system state, this system should have one input - one output
a : float
parameter of the system
b : float
parameter of the system
history_state : list
time history of state
"""
def __init__(self, a, b, init_state=0.0):
"""
Parameters
-----------
a : float
parameter of the system
b : float
parameter of the system
init_state : float, optional
initial state of system default is 0.0
"""
self.state = init_state
self.a = a
self.b = b
self.history_state = [init_state]
def update_state(self, u, dt=0.01):
"""calculating input
Parameters
------------
u : float
input of system in some cases this means the reference
dt : float in seconds, optional
sampling time of simulation, default is 0.01 [s]
"""
# solve Runge-Kutta
k0 = dt * self._func(self.state, u)
k1 = dt * self._func(self.state + k0/2.0, u)
k2 = dt * self._func(self.state + k1/2.0, u)
k3 = dt * self._func(self.state + k2, u)
self.state += (k0 + 2 * k1 + 2 * k2 + k3) / 6.0
# for oylar
# self.state += k0
# save
self.history_state.append(self.state)
def _func(self, y, u):
"""
Parameters
------------
y : float
state of system
u : float
input of system in some cases this means the reference
"""
y_dot = -self.a * y + self.b * u
return y_dot
class LyapunovMRAC():
"""LyapunovMRAC
Attributes
-----------
input : float
system state, this system should have one input - one output
a : float
parameter of reference model
alpha_1 : float
parameter of the controller
alpha_2 : float
parameter of the controller
theta_1 : float
state of the controller
theta_2 : float
state of the controller
history_input : list
time history of input
"""
def __init__(self, g_1, g_2, init_theta_1=0.0, init_theta_2=0.0, init_input=0.0):
"""
Parameters
-----------
g_1 : float
parameter of the controller
g_2 : float
parameter of the controller
theta_1 : float, optional
state of the controller default is 0.0
theta_2 : float, optional
state of the controller default is 0.0
init_input : float, optional
initial input of controller default is 0.0
"""
self.input = init_input
# parameters
self.g_1 = g_1
self.g_2 = g_2
# states
self.theta_1 = init_theta_1
self.theta_2 = init_theta_2
self.history_input = [init_input]
def update_input(self, e, r, y, dt=0.01):
"""
Parameters
------------
e : float
error value of system
r : float
reference value
y : float
output the model value
dt : float in seconds, optional
sampling time of simulation, default is 0.01 [s]
"""
# for theta 1, theta 1 dot, theta 2, theta 2 dot
k0 = [0.0 for _ in range(4)]
k1 = [0.0 for _ in range(4)]
k2 = [0.0 for _ in range(4)]
k3 = [0.0 for _ in range(4)]
functions = [self._func_theta_1, self._func_theta_2]
# solve Runge-Kutta
for i, func in enumerate(functions):
k0[i] = dt * func(self.theta_1, self.theta_2, e, r, y)
for i, func in enumerate(functions):
k1[i] = dt * func(self.theta_1 + k0[0]/2.0, self.theta_2 + k0[1]/2.0, e, r, y)
for i, func in enumerate(functions):
k2[i] = dt * func(self.theta_1 + k1[0]/2.0, self.theta_2 + k1[1]/2.0, e, r, y)
for i, func in enumerate(functions):
k3[i] = dt * func(self.theta_1 + k2[0], self.theta_2 + k2[1], e, r, y)
self.theta_1 += (k0[0] + 2 * k1[0] + 2 * k2[0] + k3[0]) / 6.0
self.theta_2 += (k0[1] + 2 * k1[1] + 2 * k2[1] + k3[1]) / 6.0
# for oylar
"""
self.theta_1 += k0[0]
self.u_1 += k0[1]
self.theta_2 += k0[2]
self.u_2 += k0[3]
"""
# calc input
self.input = self.theta_1 * r + self.theta_2 * y
# save
self.history_input.append(self.input)
def _func_theta_1(self, theta_1, theta_2, e, r, y):
"""
Parameters
------------
theta_1 : float
state of the controller
theta_2 : float
state of the controller
e : float
error
r : float
reference
y : float
output of system
"""
y_dot = self.g_1 * r * e
return y_dot
def _func_theta_2(self, theta_1, theta_2, e, r, y):
"""
Parameters
------------
Parameters
------------
theta_1 : float
state of the controller
theta_2 : float
state of the controller
e : float
error
r : float
reference
y : float
output of system
"""
y_dot = self.g_2 * y * e
return y_dot
def main():
# control plant
a = -0.5
b = 0.5
plant = FirstOrderSystem(a, b)
# reference model
a = 1.
b = 1.
reference_model = FirstOrderSystem(a, b)
# controller
g_1 = 5.
g_2 = 5.
controller = LyapunovMRAC(g_1, g_2)
simulation_time = 50 # in second
dt = 0.01
simulation_iterations = int(simulation_time / dt) # dt is 0.01
history_error = [0.0]
history_r = [0.0]
for i in range(1, simulation_iterations): # skip the first
# reference input
r = math.sin(dt * i)
# update reference
reference_model.update_state(r, dt=dt)
# update plant
plant.update_state(controller.input, dt=dt)
# calc error
e = reference_model.state - plant.state
y = plant.state
history_error.append(e)
history_r.append(r)
# make the gradient
controller.update_input(e, r, y, dt=dt)
# fig
plt.plot(np.arange(simulation_iterations)*dt, plant.history_state, label="plant y", linestyle="dashed")
plt.plot(np.arange(simulation_iterations)*dt, reference_model.history_state, label="model reference")
plt.plot(np.arange(simulation_iterations)*dt, history_error, label="error", linestyle="dashdot")
# plt.plot(range(simulation_iterations), history_r, label="error")
plt.xlabel("time [s]")
plt.ylabel("y")
plt.legend()
plt.show()
# input
# plt.plot(np.arange(simulation_iterations)*dt, controller.history_input)
# plt.show()
if __name__ == "__main__":
main()