はじめに
最適制御に取り組んでいて,たまにアルゴリズムベースの手法に出会います
差動二輪の制御だと,DWA(Dynamic Window Approach)が有名です
最近?流行ってるROSにもすでにのってます
実装したくて,がっつり原本(少し古いですが)を読み込んだので論文をまとめます
次回にpythonで実装する予定です(世の中にありふれていますが,やってみたいので!)
今回説明で、文章が多いので,面白くないかもしれませんが,自律移動ロボットに興味がある方は読んでいただけると嬉しいです
実装編をupしたのでそちらの方がいいかもです
参考
DWA論文
https://www.ri.cmu.edu/pub_files/pub1/fox_dieter_1997_1/fox_dieter_1997_1.pdf
DWAマトラボ
https://myenigma.hatenablog.com/entry/20140624/1403618922
背景
- 静的な環境を考慮した手法が多く,障害物などに会うと止まってしまうなどの手法が多い
- 動的に環境を考慮したい→ある一定時間内(予測時間)を考える手法
- 加速度制限は考えず,その一定時間内に到達できる速度で考える
- 可能な速度と回転速度から,評価関数を最小化するものを選ぶ
- 従来手法と異なるのは,モバイルロボットの運動学を考慮しているところ
ようは,いける範囲の中から,評価関数(障害物や目標を考慮した)ものを選ぶという手法です
従来手法
- 障害物回避の従来手法は大きく分けて2つでglobalとlocalが存在する
- global
- ゴールまでを計算できる
- 環境のモデルが不正確だと無理
- 計算時間がかかる
- local
- 計算量が少ない(再計算しやすい)
- 簡単に局所解に落ちる
- 従来は2段階で考えている
- ロボットのことは考えずにとりあえず,いい感じの方向を決める⇒その方向への出力を計算
- これではロボットの制約を考慮した方向が出てない(いきなり曲がれとかいう指示がでてる可能性がある)
- global
つまり,動的な環境を考えながら,かつ,ロボットのいける範囲で探索したいねということです
モデル
2輪なので以下のモデルですね
\boldsymbol{\dot{X}} =
\begin{bmatrix}
cos & 0\\
sin & 0\\
0 & 1
\end{bmatrix}
\begin{bmatrix}
u_v\\
u_w
\end{bmatrix}
状態量は,x, y, θです
予測可能範囲は各サンプリング時間の速度に依存します
この論文の式が少し変というか複雑なのは,synchro drive robotだからなようです.
僕も下記積分が上手くいかず,おかしいとおもっていました
なので,無視で,基本的には単純に一番上のモデルで良いと思います
アルゴリズムの流れ
- 空間探索
2. 軌跡を探索(角速度と速度でいけるエリアを決定)
3. 加速度制約や障害物などからいける範囲を絞る
4. ダイナミックウィンドウを作る - 最適化計算(ゴールに向いている方向,障害物との距離,まっすぐ進むことで決まる評価関数)を行う
- 入力の組み合わせを決定する
という流れです.図で書くとこんな感じ
いたってシンプルで拡張性が非常に高いと思っています
ではそれぞれの内容について述べていきます
空間探索
軌跡を探索
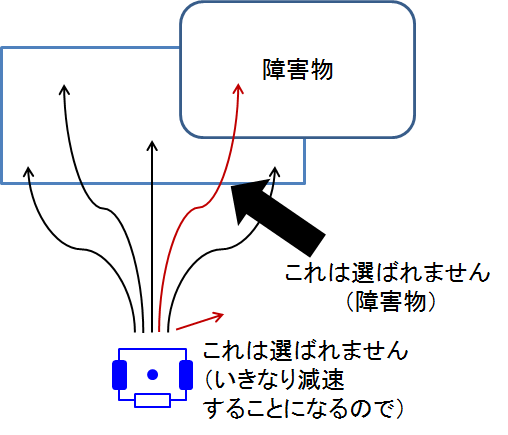
ここでのポイントは,計算量を落とすために,最初の区間以外は一定速度で進むことを考慮します(加速度が一定ということです)
⇒実はこれが結構欠点かもしれません たぶん古い手法なので提案はいろいろされていると思いますが...
イメージはこうです
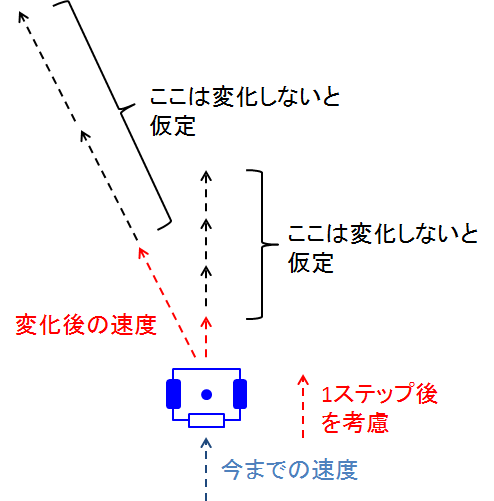
ここで,つまり,(v, ω)の組み合わせを考えていけばよいことになります.
範囲を絞る
さてここで,障害物回避や加速度制約を考えて無理なところにはいきませんね
ダイナミックウィンドウを作る
今までのを用いて,どの組み合わせの速度入力と角速度入力ならどこのエリアならすすむことができるのかを考えます
これで条件を満たす,角度,角速度を抽出します!
最適化計算
最適化計算といっても、どの組み合わせが一番いいか考えてるだけなので勾配等は用いておらず、俗に言う最適化計算ではありません
まぁでも選ばれた候補の中から全部試して選ぶので、組み合わせ最適化問題かな、、、
ようは探索しますってことです!
評価関数を説明します
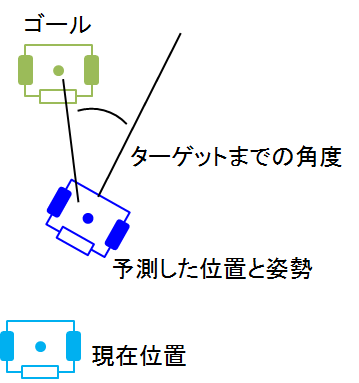
まず、向き(最終点でゴールの方向に向いてるかどうかの向きです)
なので,
(V_{opt}, \omega_{opt}) = min [\theta_{pre} - \theta_{to goal}]
次に障害物との距離
これはそのままです.
道中にある障害物の中で最も近いものとの距離
自分が通る位置は離散的に計算していいので,それと障害物との距離を計算します
(V_{opt}, \omega_{opt}) = max [(x_{obst} - x)^2+(y_{obst} - y)^2]
次にどれくらい速度が出てるかです(直線)
組み合わせとして,vが大きければ大きいほど(選べる範囲の中で)評価関数が大きくなります
(V_{opt}, \omega_{opt}) = max [v]
こうすることで、目標に限りなく向いて直線のスピードが出て、かつ障害物をかわせるようになります
でもここでポイント!
評価関数の中にたぶんあえて、目標状態との偏差はとってません
そうすると障害物回避とのバランスをとるのが難しいんでしょうか?
ようは探索型のアルゴリズムということです
目標に必ず行ってくださいという制御ではないので、モデル予測で安定性を証明してる自分としては、、、
まぁここを工夫すれば研究になるかもしれませんね
もうされてそうですけど
ここもアイディアですが
それぞれの値を正規化して評価します
G(v, \omega) = \alpha[heading](v, \omega) + \beta[distance _{object}](v, \omega)+ \gamma[velocity](v, \omega)
そうすることでスムーズに評価関数が構成されますね!
論文の中では,パラメータを考慮してます
さて以上が手法です
良い点
- 実装が楽
- 速度と加速度の制約を考慮できる
さて今までのDWAですが,良い点は実装が楽,実際の動きを考慮できる,速度と加速度の制約を陽に考慮できるってことです
最適制御において制約は最大の敵です(難易度が一気にあがります)
それをこんな簡単な形でできるのはいいですね
悪い点
- 速度一定(改善手法あるかも)
- 目的地での姿勢は考慮できない
- 組み合わせが増えると計算時間が増える
- パラメータをうまく設定しないと局所解に陥る
他にもいろいろ考えられますが,改善手法が提案されてる可能性があるので,ここまでで!
探索型のアルゴリズムとしては最高です
最後に
次回実装します!
pythonでやる予定です
あと少し量子アニーリングについて触れる機会があったのでそれも書こうと思います