この記事は東大工学部物工/計数 Advent Calendar 2019 16日目の記事です．

12月も半ばになりいよいよ年の瀬という感じが増してまいりました．東大工学部で計数工学を学んでいるマ∃太と申します．
計数工学というのは実に様々な分野を含むわけですが，その中でも今回はちょっと変わり種の「光学的フーリエ変換」を紹介したいと思います．

まえがき

光学的フーリエ変換は，光をつかってフーリエ変換が計算できる！という現象です．この記事では，かなりざっくりと（煩雑な数式を用いずに）「なんで光でフーリエ変換ができるの？」ということを説明していきます．議論の誤魔化しなどもありますので，この話題について詳しく知りたい場合には光学の教科書を読んだりこういうのを読んだりするといいと思います．

前提知識

また，あまりたくさんのことを説明しても焦点がぼやけてしまうと思いますので，この記事では，以下のことをなんとなくは知っているという人向けに書いていくことにします．

フーリエ変換について（定義式や使い道など）
オイラーの公式（$e^{i\theta} = \cos \theta + i \sin \theta$）
レンズでの実像・虚像の作図の仕方

どれも本で調べるかインターネットで検索すると解説が出てくると思うので，知らない人は適当に図書館に行くなりググるなり(Google is your teacher!)してください．
工学を学ぶ人向けのフーリエ変換についてのおすすめのサイトはやる夫で学ぶディジタル信号処理です．（計数工学科ご出身の鏡先生が執筆なさっています．）

導出

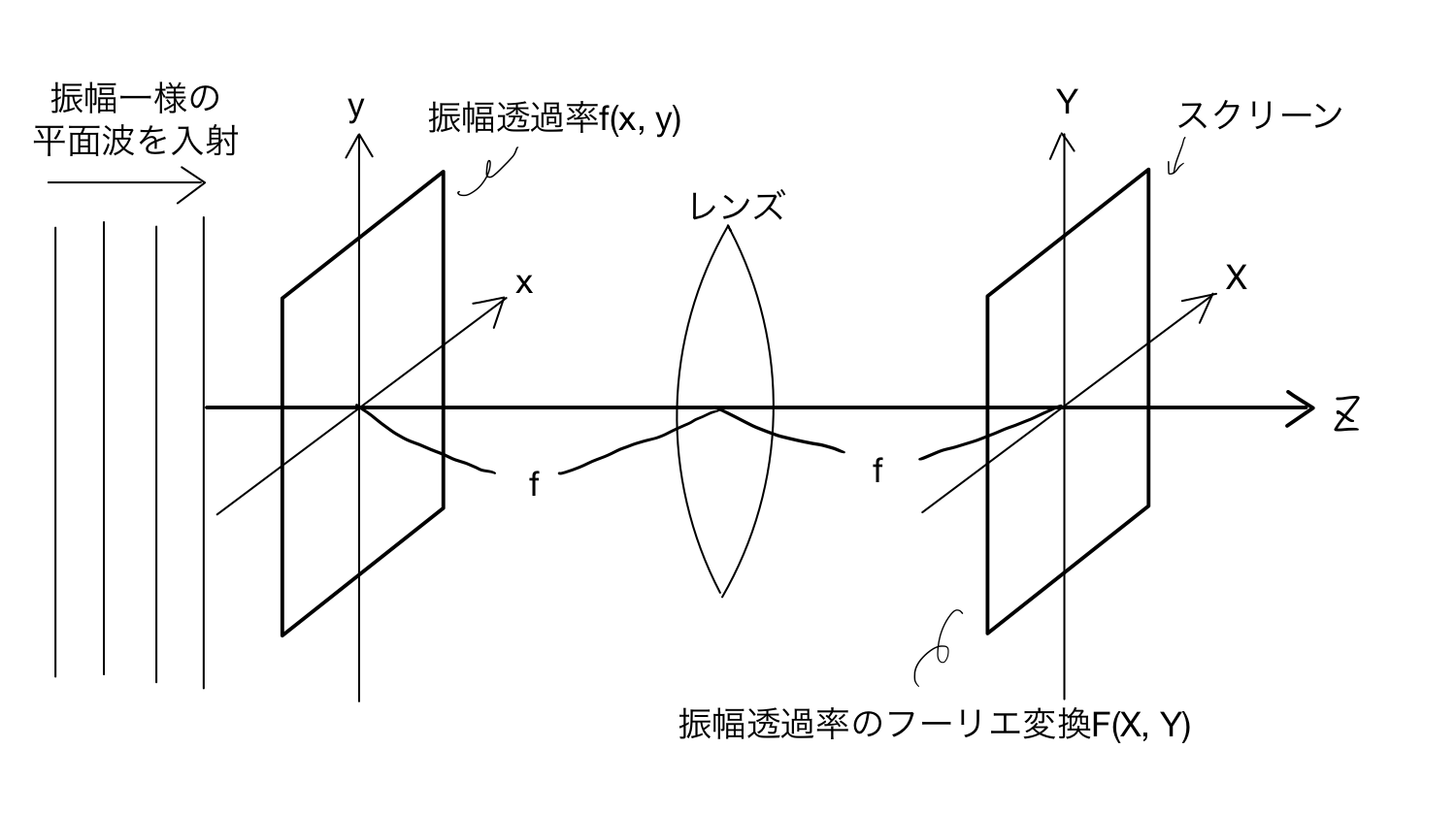
光学的フーリエ変換の簡単な導出ということで以下のような実験系を考え，手前の物体の振幅透過率の空間分布$f(x, y)$のフーリエ変換がスクリーン上に映し出されることを確認します．

実験系

以下に今回考える光学的フーリエ変換の実験系を示します．

今回は，$f(x, y)$で表される振幅透過率の空間分布を持つ2次元の物体に平面波を当ててレンズを通すことで焦点距離の位置に置いたスクリーンに$f(x,y)$の2次元フーリエ変換像$F(X,Y)$が映し出される，という実験を考えます．
$f(x, y)$で表される振幅透過率の空間分布を持つ2次元の物体とは，例えば「真ん中に半径$r$の円状の穴が空いたついたて」といったものです．この場合には

f(x) = \left\{
\begin{array}{ll}
1 & (x^2 + y^2 \leq r^2) \\
0 & (\mathrm{otherwise})
\end{array}
\right.

と表現されます．

導出の流れ

まずは光の複素振幅を導入して以降の計算の地盤を作ります．
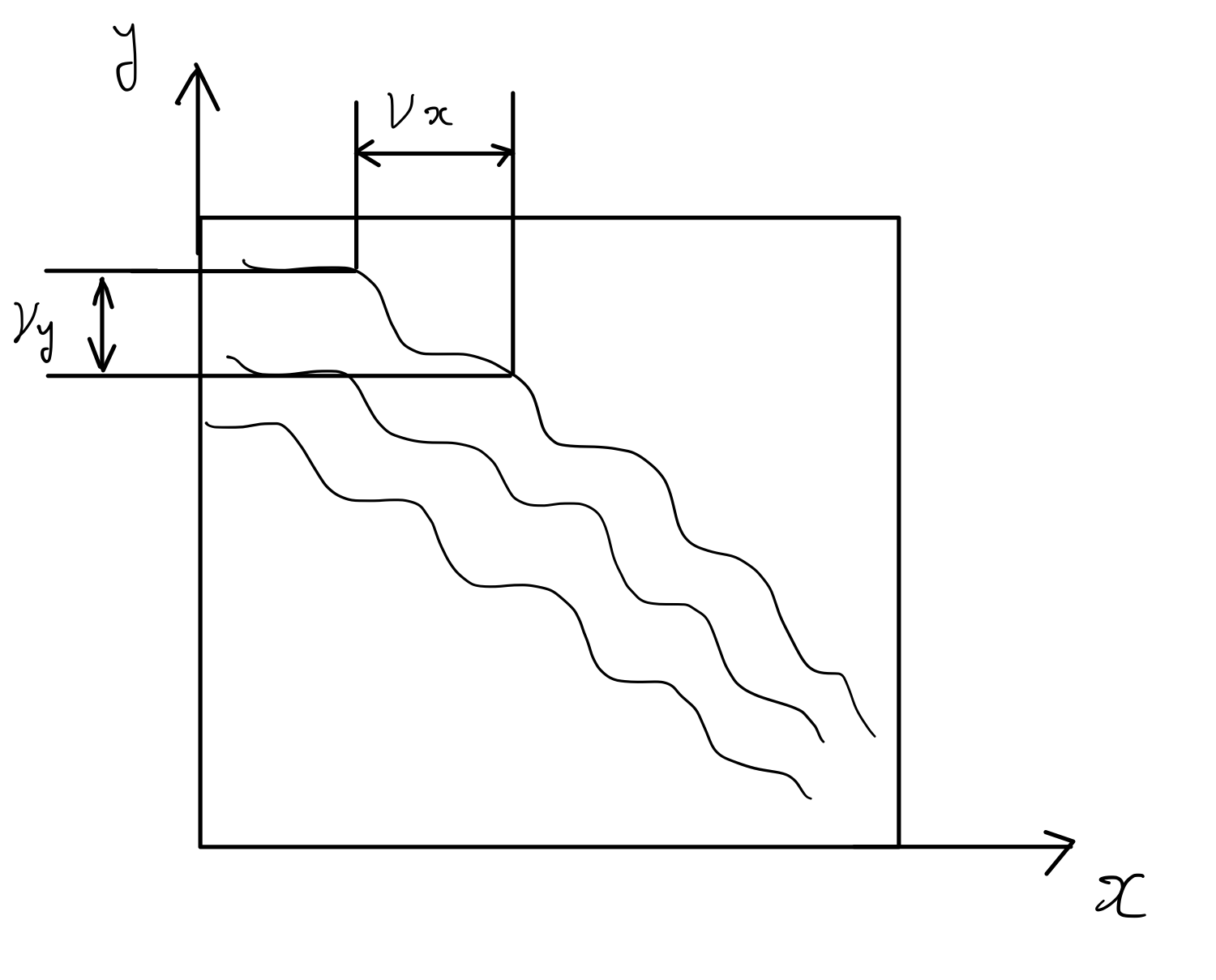
次に，物体の振幅透過率$f(x,y)$が正弦波状の振幅透過率の重ね合わせで表せると仮定し，基底として透過率が空間周波数$(\nu_x, \nu_y)$の正弦波であるような物体を考えます．この物体に振幅一様の平面波を入射したときの透過光の伝播方向を考えます．具体的には，振幅透過率の空間周波数$(\nu_x, \nu_y)$と透過光の伝播方向$(\theta_x, \theta_y)$が1対1に対応することを確認します．
最後に，レンズを用いて伝播方向$(\theta_x, \theta_y)$とスクリーン上の点$(X,Y)$が1対1に対応することを確かめます．
以上のことが全てわかると，透過率$f(x,y)$を分解したときの空間周波数$(\nu_x, \nu_y)$とスクリーン上の点$(X,Y)$が1対1に対応し，スクリーン上の光強度$I(X,Y)$というかたちで振幅透過率のフーリエ変換が観測されることがわかります．

複素振幅の導入

振幅といえば普通は実数値を思い浮かべると思いますが，以降の議論が円滑に進むように振幅を複素数に拡張した複素振幅というのを導入します．
一般に正弦波は

u(x,y,z,t) = a \cos \left\{\omega t -(k_x x + k_y y + k_z z) + \phi \right\}

と表されますが，ここに仮想的な虚数項

i\ a \sin \left\{\omega t -(k_x x + k_y y + k_z z) + \phi \right\}

を付け足して

u(x,y,z,t) = \mathcal{Re} \left[ a \exp \left[i \left\{\omega t -(k_x x + k_y y + k_z z) + \phi \right\} \right]\right]

とします．この$\mathcal{Re}$の中身のうち時間に依存しない項

U(x,y,z) = a\ \mathrm{e}^{-i(k_x x+k_y y + k_z z)+\phi}

を複素振幅と呼びます．複素振幅は，振幅と初期位相を同時に表す量です．

正弦波状の振幅透過率と透過光の伝播方向

振幅透過率が

f(x,y,z) = \mathrm{e}^{-i2\pi (\nu _x x + \nu_y y)}

であるような物質に振幅1の一様な平面波を入射するとします．このときの透過光の複素振幅を

U(x,y,z) = \mathrm{e}^{-i(k_x x+k_y y+k_z z)}

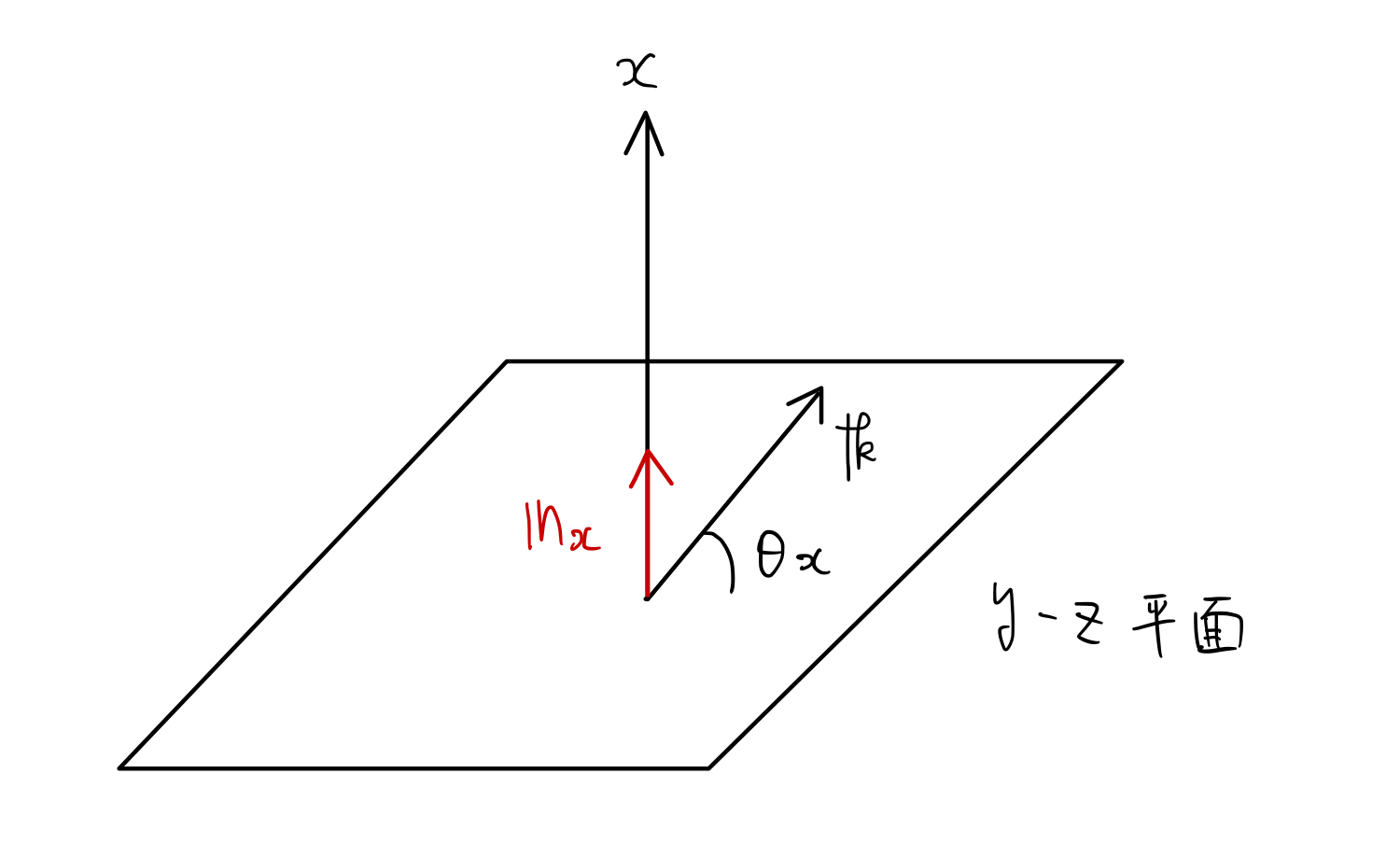
とすると，以下の図より

\vec{n_x} \cdot \vec{k} = 1 \cdot k \cdot \cos(\frac{\pi}{2} - \theta_x)\\
\mbox{（ただし，}\vec{k}=(k_x,k_y,k_z)^{\rm{T}},\ k=|\vec{k}|,\ \vec{n_x} \mbox{はx軸方向の単位ベクトル)}

となることがわかります．この両辺についてそれぞれ

(左辺) = k_x,\ (右辺) = k \sin \theta_x

が成り立つことから，

\theta_x = \sin^{-1} \frac{k_x}{k}

となることがわかります．

同様の議論から，

\theta_y = \sin ^{-1} \frac{k_y}{k}

がわかります．ここで，物体を透過した直後の透過光の複素振幅は，物体の振幅透過率に等しい（$U(x,y,0) = f(x,y)$）ということを利用して，

\left\{
\begin{array}{ll}
k_x &= 2\pi \nu_x \\
k_y &= 2\pi \nu_y
\end{array}
\right.

がいえます．この式を上で求めた伝播方向の式に代入して

\left\{
\begin{array}{ll}
\theta_x &= \sin^{-1} \lambda \nu_x \\
\theta_y &= \sin^{-1} \lambda \nu_y
\end{array}
\right.

が導かれました．これは
空間周波数が$\nu_x,\nu_y$であるような正弦波状の振幅透過率を持つ物体に振幅1の一様平面波を入射するとそのときの透過光の伝播方向$(\theta_x,\theta_y)$は一意に定まる
と言うことを意味しています．

レンズの役割

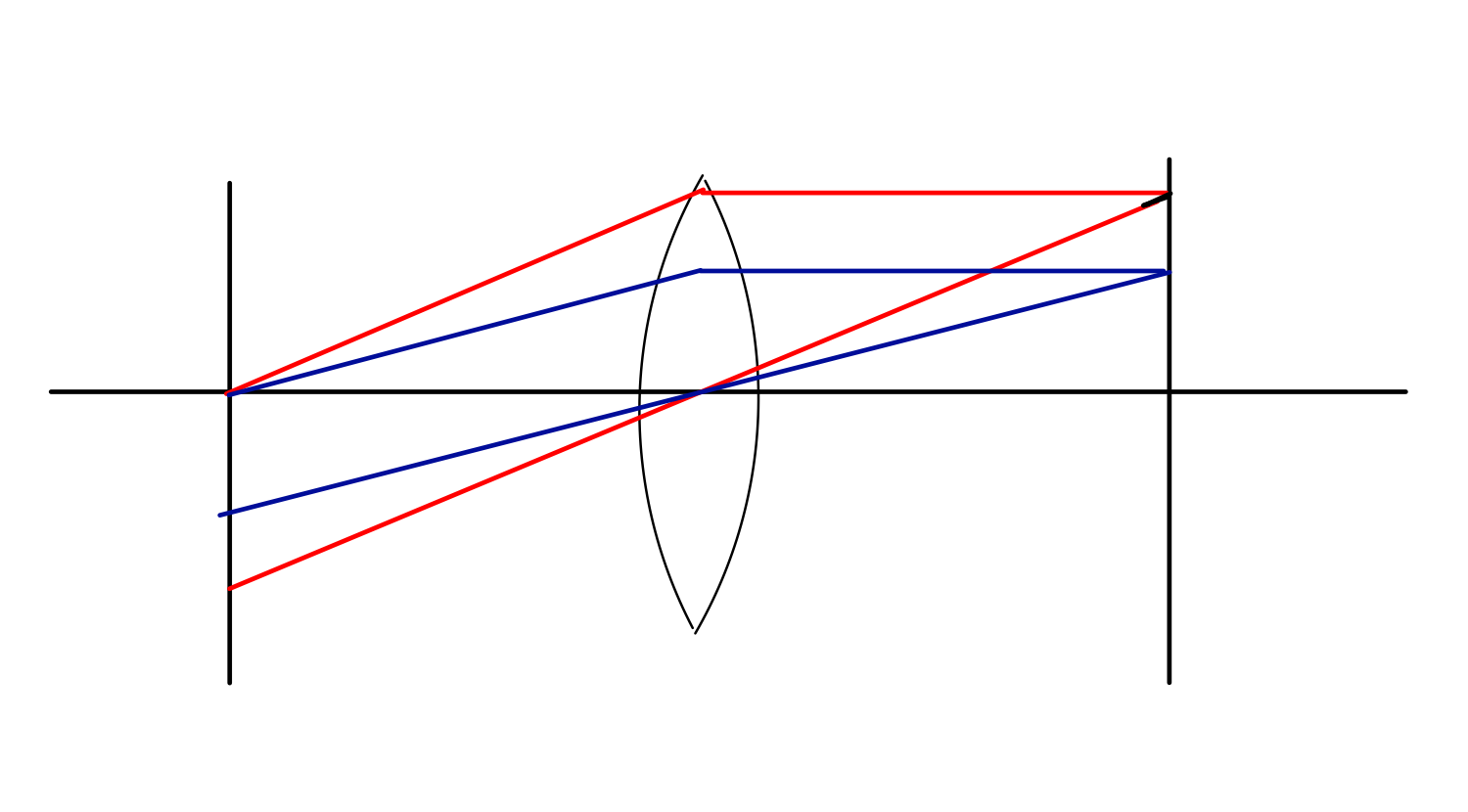
これまで見てきたように，透過光の伝播方向は対応する正弦波状の透過率の空間周波数によって決まる，ということでした．つまり，伝播方向ごとの（実数の）振幅がわかれば，物体の振幅透過率のフーリエ変換がわかるということになります．しかし，入射光と同じく透過光も平面波になっており，角度が多少違ったところで透過光同士が重なってしまって各伝播方向ごとの振幅を取り出すためには無限遠で観測しなければならないという問題点があります．
この問題点を解決するのがレンズです．凸レンズは平行光線を焦点位置に集めるという働きがあります．つまり，無限遠を焦点距離まで持ってこれるということです．以下の図を見るとわかるように，レンズを通る前は平行光（平面波）だった透過光が，焦点距離のところで角度に応じた位置に集光されるのです．このようにすると，透過光の伝播方向$(\theta_x,\theta_y)$と焦点距離のところに置いたスクリーン上の点$(X,Y)$が1対1に対応します．

結論

以上の議論から，物体の振幅透過率を正弦波で分解したときの空間周波数$\nu_x,\nu_y$とスクリーン上の点$(X,Y)$が1対1にに対応するということがわかります．つまり，スクリーン上の光強度$I(X,Y) \propto |F(\frac{x}{\lambda f},\frac{y}{\lambda f})|^2$を観測することでフーリエ変換が計算できた！ということになります．

あとがき

今回はかなりざっくりと，定性的に光学的フーリエ変換の導出をしました．もっとこの話を知りたいという人は，フラウンホーファー回折などといったキーワードで光学の教科書を探してみたり，東京大学の学生であれば物理工学科3A科目の「光学」や計数工学科3A科目の「回路学第二」を受講してみると良いと思います．
東大工学部の物理工学科，計数工学科は東京大学五月祭で「工学博覧会」という学術展示企画を行います．そこでも今回のような光にまつわる面白い展示を行う予定なので，興味のある方は是非いらしてください！

参考文献

谷田　純　『光計算』（ナチュラルコンピューティング・シリーズ　第1巻） p.40-43