1.自己紹介
はじめまして2020年4月から株式会社たき工房にエンジニアで新卒入社した@usbhatyuです。
現在はテックラボという部署でAR,VRやインタラクティブコンテンツの開発をしています。
学生の頃はProcessingやArduinoなどを使ってインタラクティブ作品を作っていました。
今はTouchDesignerやUnity、言語ではShaderやC#,Pythonなどを触っています。
2.メリークリスマス!!!
今日は12月25日クリスマス、そしてAdventCalender最終日ですね。
ということでクリスマスっぽい記事を書きました。
技術的な内容でいうとGLSLMATのVertexShaderについてです。
あんまりVertexShader単体についての記事を見かけないっていうのと、自分の知識確認という点でこの内容を選びました。
今回作るものはこちら ↓

このクリスマスツリーはモデリングしてFBXを読み込んだわけじゃなく、タイトルにもある通りVertexShaderで頂点を動かして形を作っています。
世の中にはGLSLを使ってまるでCGソフトで作ったようなクオリティの映像を作る方々がいます。
https://www.shadertoy.com/view/ld3Gz2
上記のリンクの作品はShaderだけで描画していてクオリティがエグいですが今回はそれのほんの触り部分の記事になれたらいいなと…。
toeファイルをGithubに上げていますのでこちらを見ながら記事を読んでいくといいと思います。↓
https://github.com/usbmasa/ChristmasTree
とりあえず今回の記事の内容をやって+α勉強するとこんな映像を作れるようになります。
TouchDesignerを交えたGLSL作品 ↓
GLSLオンリーの作品 ↓round関数とか使うとSF映画に出てきそうな見た目になる#GLSL #shader #creativecoding #touchdesigner pic.twitter.com/ne9vdg9i5d
— Usuba Masato (@usbhatyu) December 24, 2020
かなり竹#shader #GLSL #creativecoding pic.twitter.com/RVz4DkFSgh
— Usuba Masato (@usbhatyu) November 18, 2020
3.TouchDesignerでの下準備
正直コードを書かなくてもビジュアルプログラミングできるよ!っていうのがTouchDesignerの特徴なんですが、今回はほぼGLSLMATで記述して完結させています。
「そんなコード私書きたくないよ!」という方にもできるだけわかりやすく理解が進むような解説を心がけようと思います。
今回はわかりやすさ重視で少ないコードでツリーに見えるように作っています。
バリバリの文系出身でかつTouchもShaderも今年から触ってるような僕が分かる内容になってるのでそんなに身構える必要はありません。
今回はツリーを形作っている部分だけ主に解説します。
TouchDesigner側ではこんな風になってます。↓
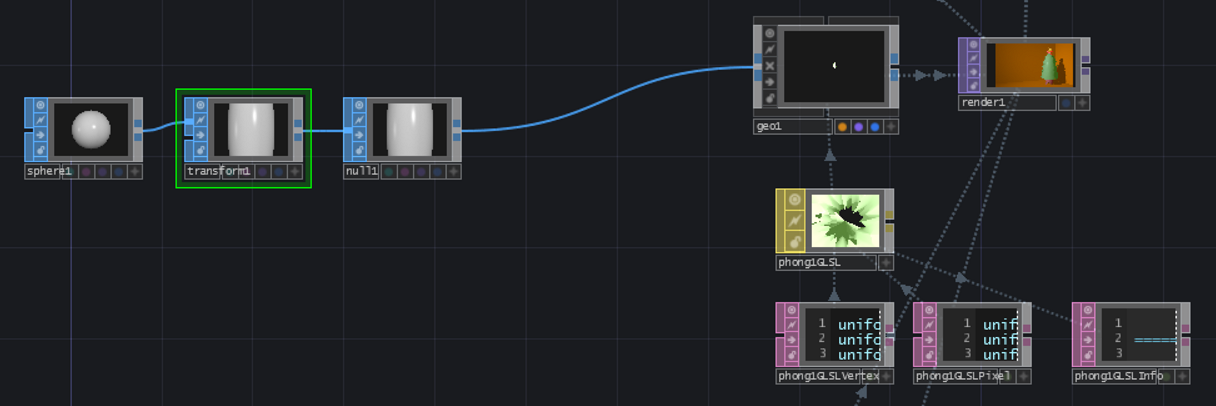
特殊なノードも一切使っておらず、めちゃくちゃシンプルな作りです。
主な変更部分はTransformSOPとGeometoryCOMPです。
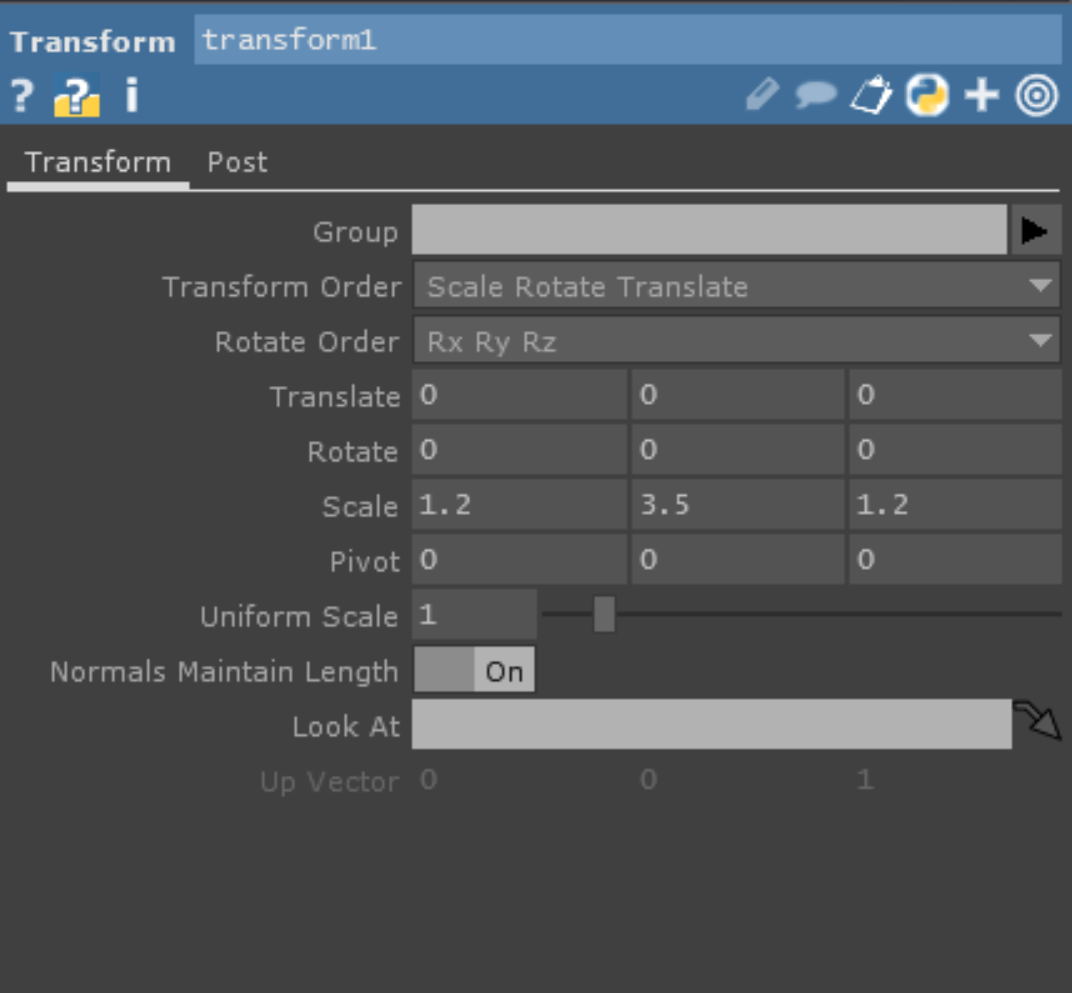
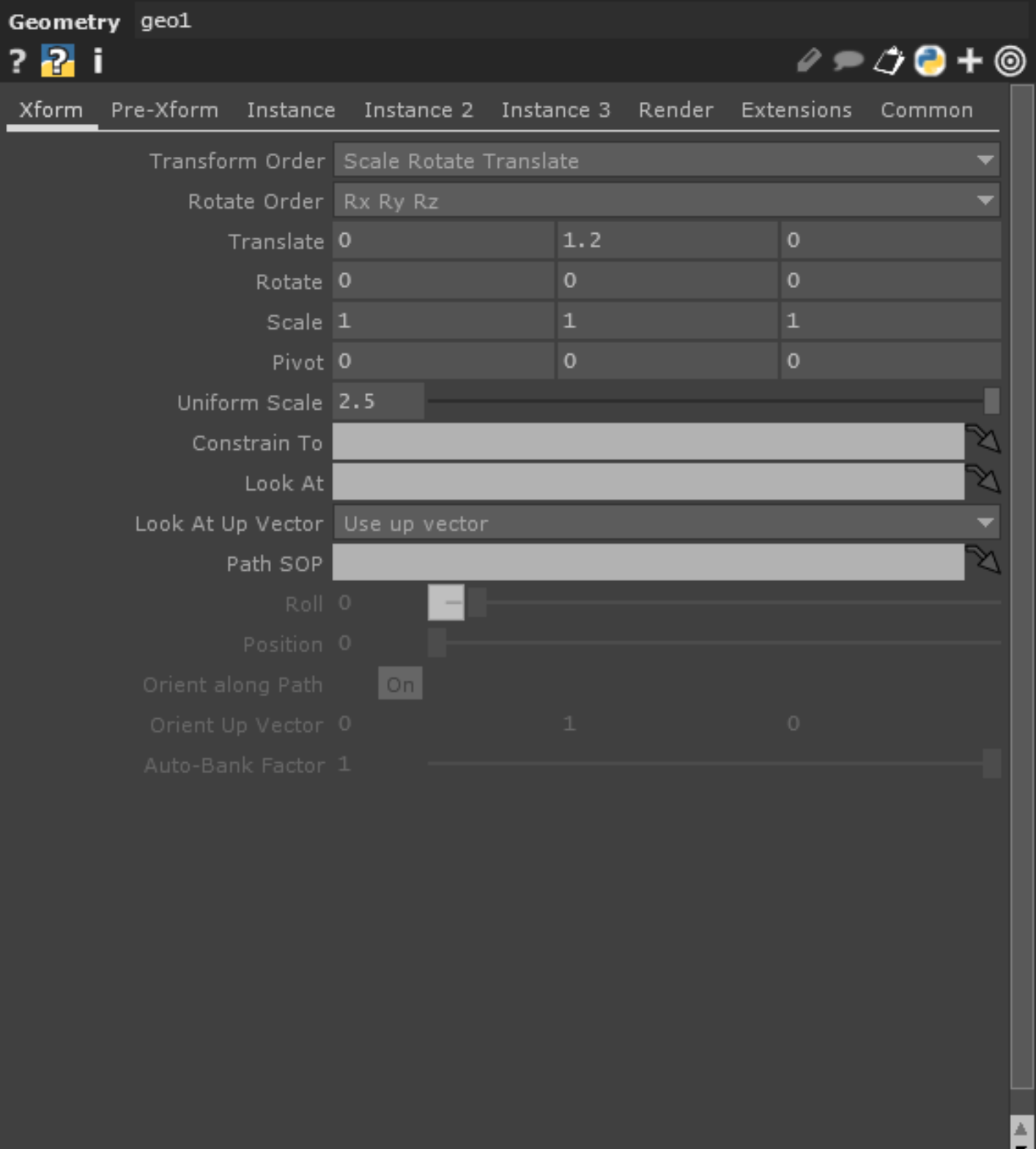
TransformSOPでツリーの形にしやすいようにSphereを楕円にしてあげてGeometoryCOMPで位置の調整をしています。
そしてGLSLMATをGeometoryCOMPにParm:Materialするのですが、本来Shaderで3D表現をするにはライティングの計算をしなくてはいけません。
しかしそこまですると大変なのでTouchにその辺はよしなにしてもらいましょう。
PhongMATのOutputShaderを押してGLSLMATを作ります。
(PhongMATのパラメーターはデフォルトのままで大丈夫です。)
これでライティングの計算をTouch側でやってもらいつつVertexShaderをいじれる状態になりました。
4.クリスマスツリーをVertexShaderで形作る
いよいよVertexShaderの記述です。
早速全体のコードを見てみましょう。
uniform vec4 uDiffuseColor;
uniform vec4 uAmbientColor;
uniform vec3 uSpecularColor;
uniform float uShininess;
uniform float uShadowStrength;
uniform vec3 uShadowColor;
out Vertex
{
vec4 color;
vec3 worldSpacePos;
vec3 worldSpaceNorm;
flat int cameraIndex;
} oVert;
out vec4 uvColor; //座標情報をPixelShaderに送る
float reafVector(vec3 p){
return step(-0.4,p.y); //葉を付ける方向を定義
}
float reafGenerate(vec3 p){
return length(sin(p*28.0)); //葉を生成
}
float reafStack(vec3 p){
return step(-0.4,p.y)*length(fract(cos(p)*17.0)); //葉の重なり具合調整
}
float treePot(vec3 p){
return step(0.5,-p.y)*length(cos(p*3.0)); //鉢を生成
}
float rootCut(vec3 p){
return step(-2.0,p.y); //鉢の下から飛び出てる余分な部分を削除
}
void main()
{
vec3 newP = P; //newPに頂点座標の情報を持ってるPを代入
//以下関数呼び出し
float distance = reafVector(newP);
distance *= reafGenerate(newP);
distance += reafStack(newP);
distance += treePot(newP);
distance *= rootCut(newP);
vec4 worldSpacePos = TDDeform(newP*distance); //上記の関数の計算を終えたdistanceを掛ける
uvColor = vec4(normalize(worldSpacePos)); //ワールド座標を正規化したものをuvColorに代入
// First deform the vertex and normal
// TDDeform always returns values in world space
vec3 uvUnwrapCoord = TDInstanceTexCoord(TDUVUnwrapCoord());
gl_Position = TDWorldToProj(worldSpacePos, uvUnwrapCoord);
// This is here to ensure we only execute lighting etc. code
// when we need it. If picking is active we don't need lighting, so
// this entire block of code will be ommited from the compile.
// The TD_PICKING_ACTIVE define will be set automatically when
// picking is active.
# ifndef TD_PICKING_ACTIVE
int cameraIndex = TDCameraIndex();
oVert.cameraIndex = cameraIndex;
oVert.worldSpacePos.xyz = worldSpacePos.xyz;
oVert.color = TDInstanceColor(Cd);
vec3 worldSpaceNorm = normalize(TDDeformNorm(N));
oVert.worldSpaceNorm.xyz = worldSpaceNorm;
# else // TD_PICKING_ACTIVE
// This will automatically write out the nessessary values
// for this shader to work with picking.
// See the documentation if you want to write custom values for picking.
TDWritePickingValues();
# endif // TD_PICKING_ACTIVE
}
一見長く見えますがほとんどPhongMATからOutputShaderした時に自動で記述されているもので、実際に自分で記述している部分はコメントアウトが書いてある箇所だけです。
重要なのは下記の五つの関数です。↓
float reafVector(vec3 p){
return step(-0.4,p.y);
}
float reafGenerate(vec3 p){
return length(sin(p*28.0));
}
float reafStack(vec3 p){
return step(-0.4,p.y)*length(fract(cos(p)*17.0));
}
float treePot(vec3 p){
return step(0.5,-p.y)*length(cos(p*3.0));
}
float rootCut(vec3 p){
return step(-2.0,p.y);
}
この関数を呼び出してる部分がここ。↓
float distance = reafVector(newP);
distance *= reafGenerate(newP);
distance += reafStack(newP);
distance += treePot(newP);
distance *= rootCut(newP);
この関数を呼び出してる部分を一旦全部コメントアウトして、上からコメントアウトを外していくとツリーが形作られていく過程が見られます。
上から順番に見て行きましょう。
一つ目のreafVectorという関数は名前の通り葉が付く方向を定義させています。
float reafVector(vec3 p){
return step(-0.4,p.y);
}
ここで使われているstep関数は第一引数の閾値より第二引数の値が下回っていたら0.0を返し、上回っていたら1.0を返す関数です。
簡単に図解をします。
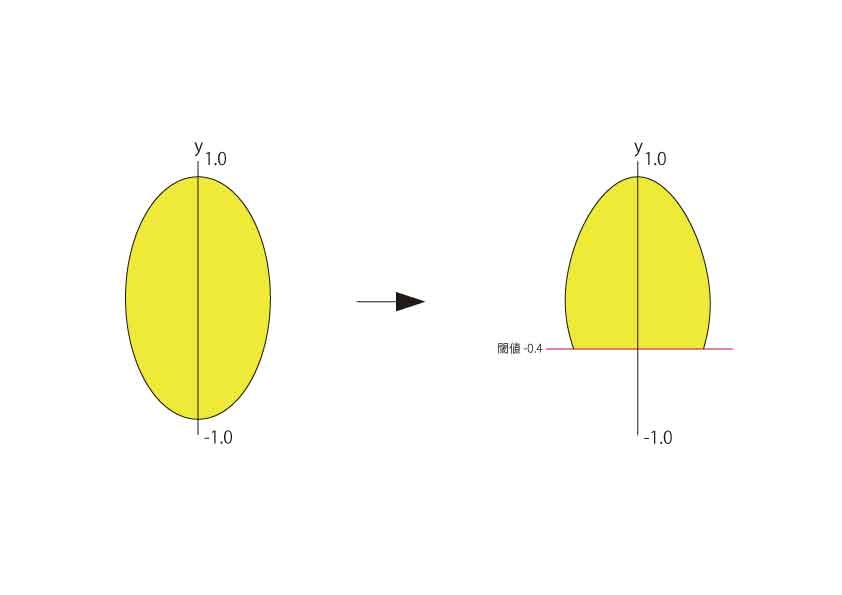
pにはnewPから渡されたGeometory内のXYZの座標情報が入っています。
第二引数にはp.yが入っているのでY軸だけに注目します。
このY軸を第一引数の閾値を基準に1.0か0.0で返します。
これによって葉が付く方向を定義できました。

続いて二つ目reafGenerateという関数を見てみましょう。
float reafGenerate(vec3 p){
return length(sin(p*28.0));
}
まず注目する部分はsin関数ですね。
sin関数はTouchのWAVECHOPにもあるのでなじみ深いかもしれません。
1.0と-1.0の間を行ったり来たりして波を作り出します。
sin波,cos波解説 ↓
https://cognicull.com/ja/uexlhxmj
sin関数の引数にはpが入っています。
一つ目のreafVector関数ではp.yでY軸の情報だけを計算していましたが今回はXYZの座標全てに計算を行います。
分かりやすくするためにx,y,zそれぞれの軸でsin波を起こした画像を並べます。


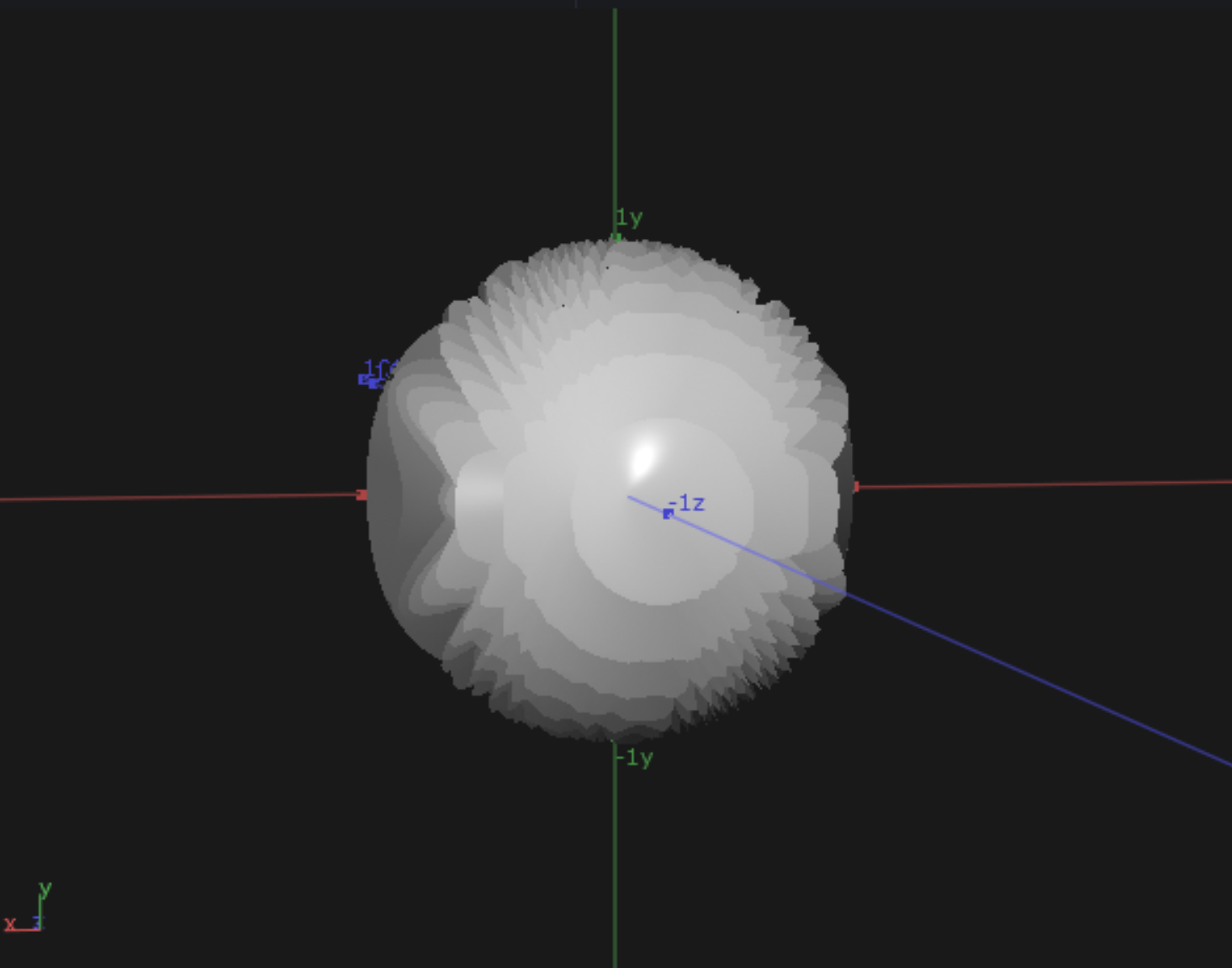
数値的には外側が1.0または-1.0、中心が0.0です。
乗算では0.0は何を掛けても0.0のままです。
なのでこの三つを掛け合わせたとき一回でも0.0が掛けられている頂点は窪み、0.0が一度も掛けられなかった頂点だけが外側に盛り上がり棘を作り出します。
(厳密には掛けているわけではないのですが感覚はこれです。)

要するに細かい波をXYZのそれぞれの軸で作ってあげその重なりでとげとげの葉を再現しているという感じですね。
これくらいならTouchでShaderを使わなくても再現はできるでしょう。
しかしGLSLはGPUで動きます。
SOPやCHOPはCPUで動くので頂点をアニメーション等させるには頂点数にかなり制限がかかります。
GPUで動かしてあげる場合より多くの頂点数を動かせリッチな映像を作ることができます。
ちなみにこのクリスマスツリーの頂点数は約18万くらいあります。
最後にLength関数を使っていますが、Lengthに関しては中に入ってるvec2型やvec3型をfloat型で返してあげる役割なんだくらいにここでは思っておいてください。
Length関数は原点(0.0)からの距離を返す関数です。
つまりsin関数などで動かした各頂点と原点(0.0)との距離をfloat型で返しています。
これで葉のギザギザを作り出すことができました。

三つ目のreafStack関数を見てみましょう。
ここまでの計算では葉がギザギザになってはいるものの均等な長さで丸みを帯びています。
なので今度はツリーの葉の重なり具合というか段々の感じをここで作り出しています。
さてコードを見てみましょう。
float reafStack(vec3 p){
return step(-0.4,p.y)*length(fract(cos(p)*17.0));
}
上の二つよりも少し複雑ですね、落ち着いて考えてみましょう。
最初のstep関数はreafVector関数で記述されているものと全く同じです。
つまりこれです。↓

膨らんでいる部分は1.0で、下のスパっと無くなっている部分は0.0です。
つまりこれに何かを掛けたとしても形の変化が起こせるのは1.0の膨らみ部分だけで、0.0の部分は何を掛けても0.0なので無変化になります。
ここでのstep関数はそういう変化させたい部分と変化させたくない部分を分ける役割をしています。
次にcos関数に注目します。
ここでも表面に波を作っているのですが二つ目のreafGenerate関数の数式と違う部分があります。
length(sin(p*28.0));
length(fract(cos(p)*17.0));
主に違う部分は二点
・数字も違うのですがそれが掛けられている場所。
・fract関数が使われていること。
いきなり数字の動き方を説明するとかなりややこしくなりそうなのでこの二つの数式の結果を比較してみましょう。


どうでしょうか?かなり違いますね。
図解してより詳しく見てみましょう。
※グラフはわかりやすいように厳密には作ってません。
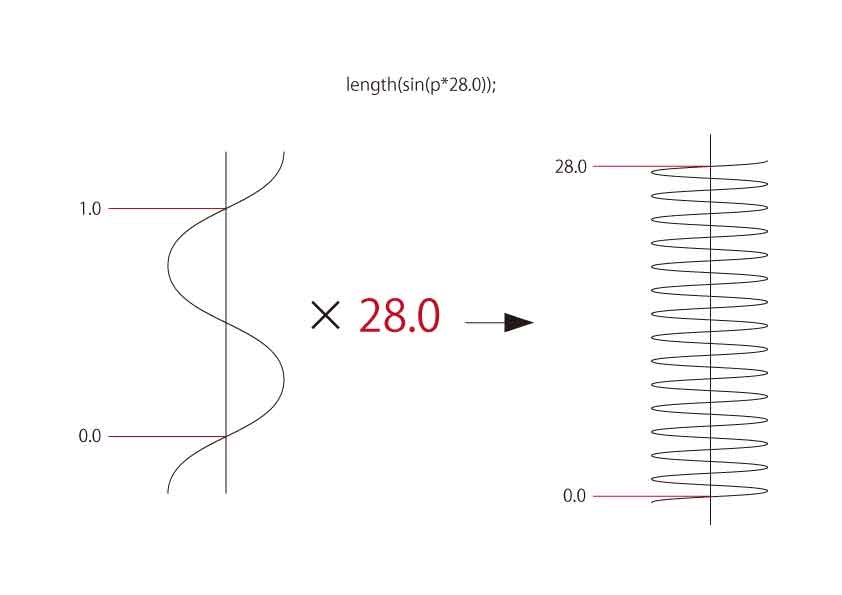
上記のpに先に数字を掛けている方は同じ波の数が増えているだけなので葉の先端が均一になります。
毛並みなどのふさふさ感を出したい時はいいでしょう。
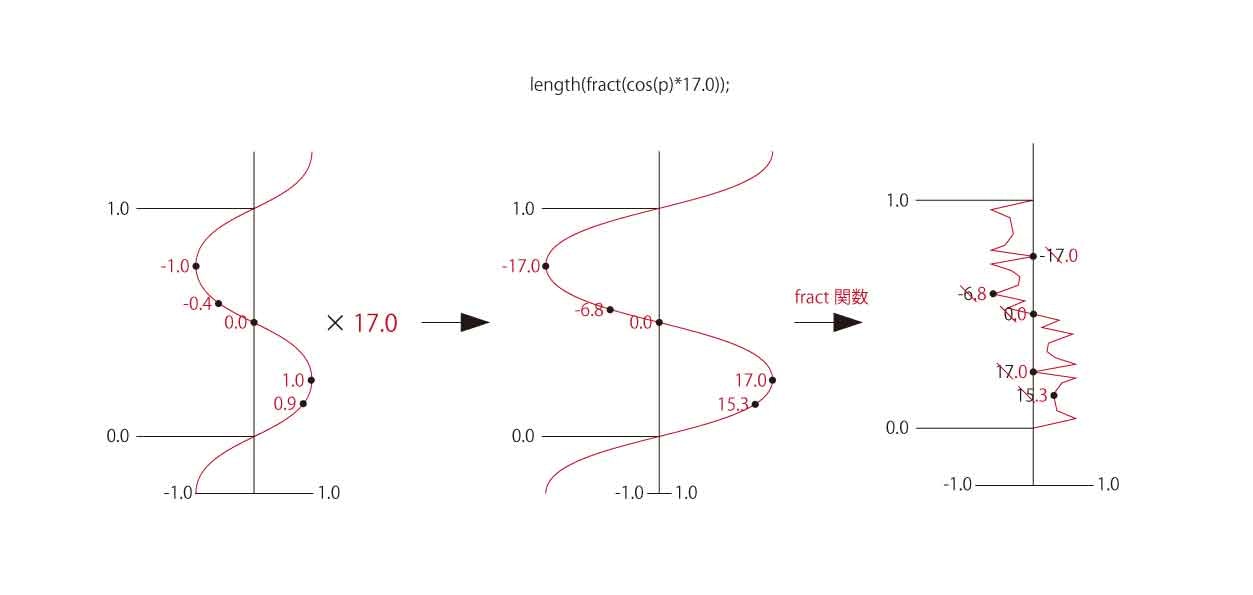
波を作った後に数字を掛けているものは波の頂点(-1.0,-0.9,-0.8…~1.0)のそれぞれに数字を掛けて小数点以下にばらつきを持たせます。
ただこの状態ではまだ表面は滑らかでかつ大きな数字を掛けたのでオブジェクトが大きくなってしまっています。
表面に凹凸を作るには先ほどの掛け算でばらつきを持たせた小数点以下の情報だけが欲しいのでfract関数を使います。
fract関数は引数の小数点以下を返す関数です。
これで凹凸を作りつつ大きくなってしまったオブジェクトを-1.0~1.0の間に収めることができます。
色々書いてますが乱数生成を行っているということです。
最後に一つ注目する部分があります。
これまでの二つと違いこの関数で返ってきた数値はdistanceに足しています。
distance += reafStack(newP);
これまでに作った葉のトゲトゲは残し生かしつつ頂点を形に合わせて伸ばしてあげている感じですね。
この場面では掛けても足しても葉の形が変わるくらいですが、次の工程では形が大きく変わってしまう可能性があります。
それについては四つ目の関数の時に説明しようと思います。
さてここまでの三つの関数でクリスマスツリーの葉の部分が完成しました…!

四つ目のtreePot関数は鉢の部分を作っていきます。
ここからのコードはほぼ説明済みのものばかりなのでリラックスしていきましょう。
コードがこちら ↓
float treePot(vec3 p){
return step(0.5,-p.y)*length(cos(p*3.0));
}
step関数はもう二回出てきていますが先ほど作っていたものとは逆で葉より下の部分を1.0にしている状態です。
コードをよく見てみるとp.yの前に-(マイナス)が付いています。
これはp.yに-1.0を掛けているということです。
図解してみます。
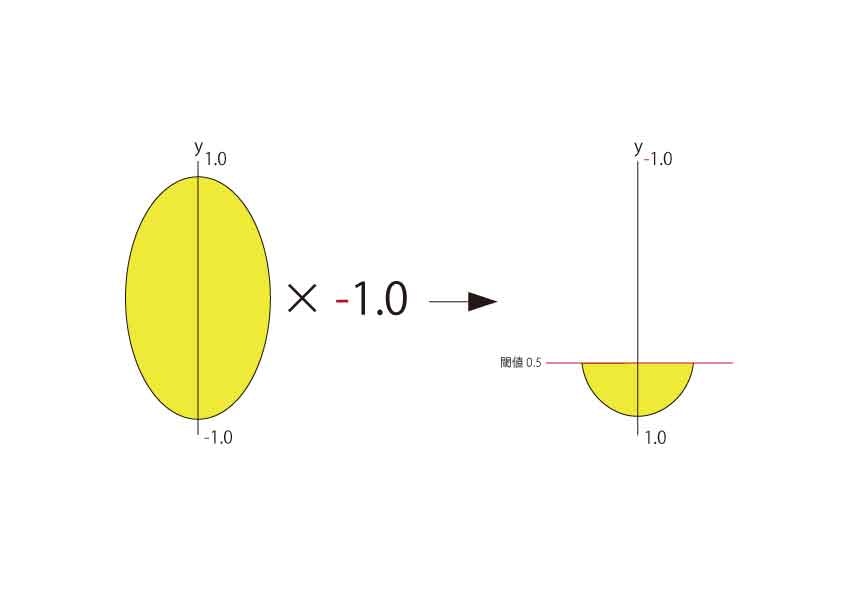
中学一年生ぐらいで習った正の数に負の数を掛けると負の数になり、負の数に負の数を掛けると正の数になります。
このように-1.0を掛ける前ではY座標は上に行くほど数字が大きくなっていきますが、掛けた後では上下関係が逆になっています。
よって下が膨らんだ状態になります。
そのstep関数に掛けられている数式がこちら ↓
length(cos(p*3.0));
今回はreafGenerate関数と同じくpに数字を掛けてから波を作っています。
しかし今回は3.0とそれほど大きな数字を掛けていないためトゲトゲになるわけではなく流線型を描いたちょうどいい鉢のような形をしています。
今回もこの関数から帰ってきた値をdistanceに足してあげています。
※step関数で葉の部分を0.0にしているのでここで掛けてしまうと今まで作った葉に0.0が掛けられて無くなってしまうので注意してください。
これでもうクリスマスツリーができたと言っても過言ではない状態まできましたね。

最後の五つ目のrootCut関数は仕上げみたいなものです。
今の状態で鉢の下の部分に出っ張りができてしまっています。
今回は不要な部分を消したいのでstep関数でその部分を0.0にして掛けてあげます。
一応コードを載せます ↓
float rootCut(vec3 p){
return step(-2.0,p.y);
}
さてこれでSphereから頂点を動かしてクリスマスツリーを作ることができました…完成!!!

5.PixelShaderで色も付けよう
はい、形ができたのも束の間ですがやはり色は付けたいですよね。
なので簡単にですが葉の部分、鉢の部分の二つに色を付けてあげましょう。
コードはこちら ↓
uniform vec4 uDiffuseColor;
uniform vec4 uAmbientColor;
uniform vec3 uSpecularColor;
uniform float uShininess;
uniform float uShadowStrength;
uniform vec3 uShadowColor;
in Vertex
{
vec4 color;
vec3 worldSpacePos;
vec3 worldSpaceNorm;
flat int cameraIndex;
} iVert;
in vec4 uvColor; //VertexShaderから座標情報を受け取る。
// Output variable for the color
layout(location = 0) out vec4 oFragColor[TD_NUM_COLOR_BUFFERS];
void main()
{
// This allows things such as order independent transparency
// and Dual-Paraboloid rendering to work properly
TDCheckDiscard();
vec4 reafColor = vec4(0.0, 0.3, 0.0, 0.0); //葉の色
vec4 trunkColor = vec4(0.2, 0.0431, 0.0, 0.0); //鉢の色
vec3 diffuseSum = vec3(0.2549, 0.0784, 0.0784);
vec3 specularSum = vec3(0.1, 0.1, 0.1);
vec3 worldSpaceNorm = normalize(iVert.worldSpaceNorm.xyz);
vec3 normal = normalize(worldSpaceNorm.xyz);
vec3 viewVec = normalize(uTDMats[iVert.cameraIndex].camInverse[3].xyz - iVert.worldSpacePos.xyz );
// Flip the normals on backfaces
// On most GPUs this function just return gl_FrontFacing.
// However, some Intel GPUs on macOS have broken gl_FrontFacing behavior.
// When one of those GPUs is detected, an alternative way
// of determing front-facing is done using the position
// and normal for this pixel.
if (!TDFrontFacing(iVert.worldSpacePos.xyz, worldSpaceNorm.xyz))
{
normal = -normal;
}
// Your shader will be recompiled based on the number
// of lights in your scene, so this continues to work
// even if you change your lighting setup after the shader
// has been exported from the Phong MAT
for (int i = 0; i < TD_NUM_LIGHTS; i++)
{
vec3 diffuseContrib = vec3(0);
vec3 specularContrib = vec3(0);
TDLighting(diffuseContrib,
specularContrib,
i,
iVert.worldSpacePos.xyz,
normal,
uShadowStrength, uShadowColor,
viewVec,
uShininess);
diffuseSum += diffuseContrib;
specularSum += specularContrib;
}
//以下のコードで二つの色にライティングの計算をしていく。
//変更箇所に///を記述
// Final Diffuse Contribution
diffuseSum *= uDiffuseColor.rgb * iVert.color.rgb;
vec3 finalDiffuse = diffuseSum;
reafColor.rgb += finalDiffuse;///
trunkColor.rgb += finalDiffuse;///
// Final Specular Contribution
vec3 finalSpecular = vec3(0.0);
specularSum *= uSpecularColor;
finalSpecular += specularSum;
reafColor.rgb += finalSpecular;///
trunkColor.rgb += finalSpecular;///
// Ambient Light Contribution
reafColor.rgb += vec3(uTDGeneral.ambientColor.rgb * uAmbientColor.rgb * iVert.color.rgb);///
trunkColor.rgb += vec3(uTDGeneral.ambientColor.rgb * uAmbientColor.rgb * iVert.color.rgb);///
// Apply fog, this does nothing if fog is disabled
reafColor = TDFog(reafColor, iVert.worldSpacePos.xyz, iVert.cameraIndex);///
trunkColor = TDFog(trunkColor, iVert.worldSpacePos.xyz, iVert.cameraIndex);///
// Alpha Calculation
float alpha = uDiffuseColor.a * iVert.color.a ;
// Dithering, does nothing if dithering is disabled
reafColor = TDDither(reafColor);///
trunkColor = TDDither(trunkColor);///
reafColor.rgb *= alpha;///
trunkColor.rgb *= alpha;///
// Modern GL removed the implicit alpha test, so we need to apply
// it manually here. This function does nothing if alpha test is disabled.
TDAlphaTest(alpha);
reafColor.a = alpha;///
trunkColor.a = alpha;///
//Y座標が-0.3以上ならreafColor、-0.3以下ならtrunkColor
if(uvColor.y >= -0.3){
oFragColor[0] = TDOutputSwizzle(reafColor);
}else{
oFragColor[0] = TDOutputSwizzle(trunkColor);
}
// TD_NUM_COLOR_BUFFERS will be set to the number of color buffers
// active in the render. By default we want to output zero to every
// buffer except the first one.
for (int i = 1; i < TD_NUM_COLOR_BUFFERS; i++)
{
oFragColor[i] = vec4(0.0);
}
}
こちらも一見長いですがほとんど自動で記述されたものばかりです。
元となる色の変数を二つ作ってライティングの計算を順次書き換え、追加しています。
自分で記述したものはコメントアウトが付いています。
一点気を付けるのはVertexShaderとPixelShaderで座標情報を共有してあげる必要があるくらいです。
変数の共有は下記のコードをそれぞれのShaderに記述してあげます。
out vec4 uvColor;
in vec4 uvColor;
その座標のY軸の情報を使って閾値より下なら茶色、上なら緑というような記述になっています。
さてこれで間違いなくクリスマスツリーの完成です…!

6.装飾などについて
最初の画像には星やリボンみたいな装飾が付いていましたがあれもVertexShaderで作られています。
基本クリスマスツリーで使っているような計算式や考え方なので今回は解説しませんが気になった方はサンプルファイルを見て計算式を読んでみてください。
ちょっとだけ言うとTorusSOPを使ってるので少し複雑な形に見えているだけです。
Sphereのオーナメントはインスタンシングでそれっぽく付けてます。
7.まとめ
僕もまだまだ勉強中なので理解が甘い部分がたくさんあります。
今回この記事を書いてる最中に@doxasさんのGLSLスクールを受けさせていただいていたんですが、知識確認や概念的な部分を勉強しながらの記事作成だったので、自分の中ではGLSL熱がホットな状態で書けたと思っています。
(解説の仕方がdoxasさんに若干影響受けてる気がします…笑)
図解とか作るの結構大変でハイカロリーな記事だったので高頻度で出すには厳しそうですが、またいつか機会があれば自分の勉強になるし書こうかなと思います。
以上アドカレ最終日の記事でした。
メリークリスマス!!良いお年を!!