単回帰分析における最小二乗誤差について

　はじめに

　最小二乗誤差、残差、、
　これらの言葉は聞いたことがある、、
　でも何を指している言葉なのか、どのように利用されているのか曖昧な方も多いと思います。
　なので今回はこれらの言葉を説明していきたいと思います
　簡単のため今回は単回帰しか触れません、重回帰は次回の記事で触れます。
　今回は単回帰についての説明は省きますね
　もしわからない方は単回帰について学んでから読んでいただけると理解が深まると思います
　では学んでいきましょう！！

　単回帰における最小二乗誤差について

　まずは最小二乗誤差についてみていきましょう
　ですが、その前に**「誤差」**について知っておく必要があります
　**「誤差」**とは、実際の目標値と回帰を利用して予測した値の差のことです。「差」なので絶対値を取ります。
　図式と数式でみていきましょう

　ちょっと(だいぶ)画質荒いですが許してください笑
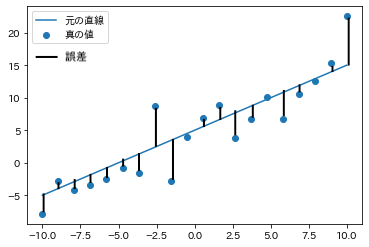
　青点が実際に観測されている点で青の実線が近似曲線になっています
　ここでいうと**「誤差」**は黒直線部分になります
　さて、これを数式化させてみていきましょう

誤差:error \\
実際の(真の)値:t_i\\
単回帰式:wx + b\\
誤差は以下式で与えられます\\
error = |t_i - (wx + b)|\\

　
　上記のように与えられますね
　なんですけど、結局は**「誤差」を最小化させたいですよね。これを「最適化」っていうんですけど最適化するには絶対値って邪魔ですよね。いちいち中身の正負を見ないといけないですから。なので二乗しましょうとします。
　ってして生まれるのが「二乗誤差」になります。
　で、全部の事象においての「二乗誤差」を足しあわせてこれを最小化させたとします。
　そうすると、二乗誤差の和が最小値になる、つまり最も当てはまりが良くなりますよね。これが「最小二乗誤差」**になるわけです。つまり最小二乗誤差の数式は以下のように表されます。

最小二乗誤差:E(w) \\
実際の(真の)値:t_i\\
単回帰式:wx + b\\
データ数:N\\
最小二乗誤差は以下のように与えられます\\

E(w) = \frac{1}{N}\Sigma_{i = 1}^{N}(t_i - (wx_i + b))^2

　で少し数式見て欲しいんですけど我々が決めなきゃいけないのはwとbだけですね。

　残差について

　**「残差」というものを押さえておきましょう。
　これは最小二乗法の代数的法則についての説明に使われるのですが、先に触れておきます。
　一部最小化についてのお話が出てくるので普通順番は逆なんですけど、こちらはあまり複雑にならないので先に説明をして肩慣らしをしてもらおうと思います。

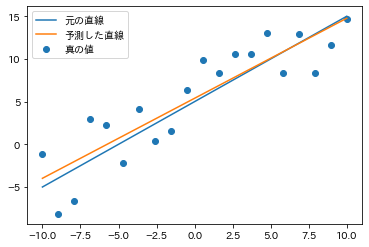
　この図は前の章で紹介したのと同じものになります。ただ、乱数入れてるので真の値の部分の分布が若干異なります。
　さっきは青の直線(元の直線、真の回帰式)　との差を見ていましたが今回は予測した直線との差を見ます。
以下の図のような感じですね

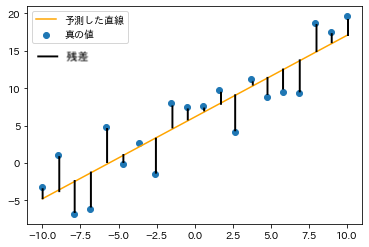
　この差が「残差」**と呼ばれます。そして残差には大きく3つの特徴があります。
　　一つ目は総和が0になること
　　二つ目は説明変数と残差の積和が0になること
　　三つ目は推定値(t_i)と残差が無相関であること

　残差の総和が0になるってことだけは肩慣らしとして証明します

　字が下手なのは許してください、、笑
　まあ、これで残差の総和が0になることがわかりましたね
　説明変数と残差の積和が0になることは相関係数が0であることを示しています。これはwの方で微分してあげれば同じ形で証明が可能です。こちらは今回省略させていただきます。

　単回帰における最小二乗誤差の最適化

　それじゃ本題です
　最小二乗誤差の最適化(最小化)について考えましょう
　先ほどの手書きの証明部分にもありましたが、w^とb^(^は「ハット」だと思ってください)についての微分がそれぞれ0になるようなw^とb^を求めましょ、という話です。これも手書きで失礼しますね。


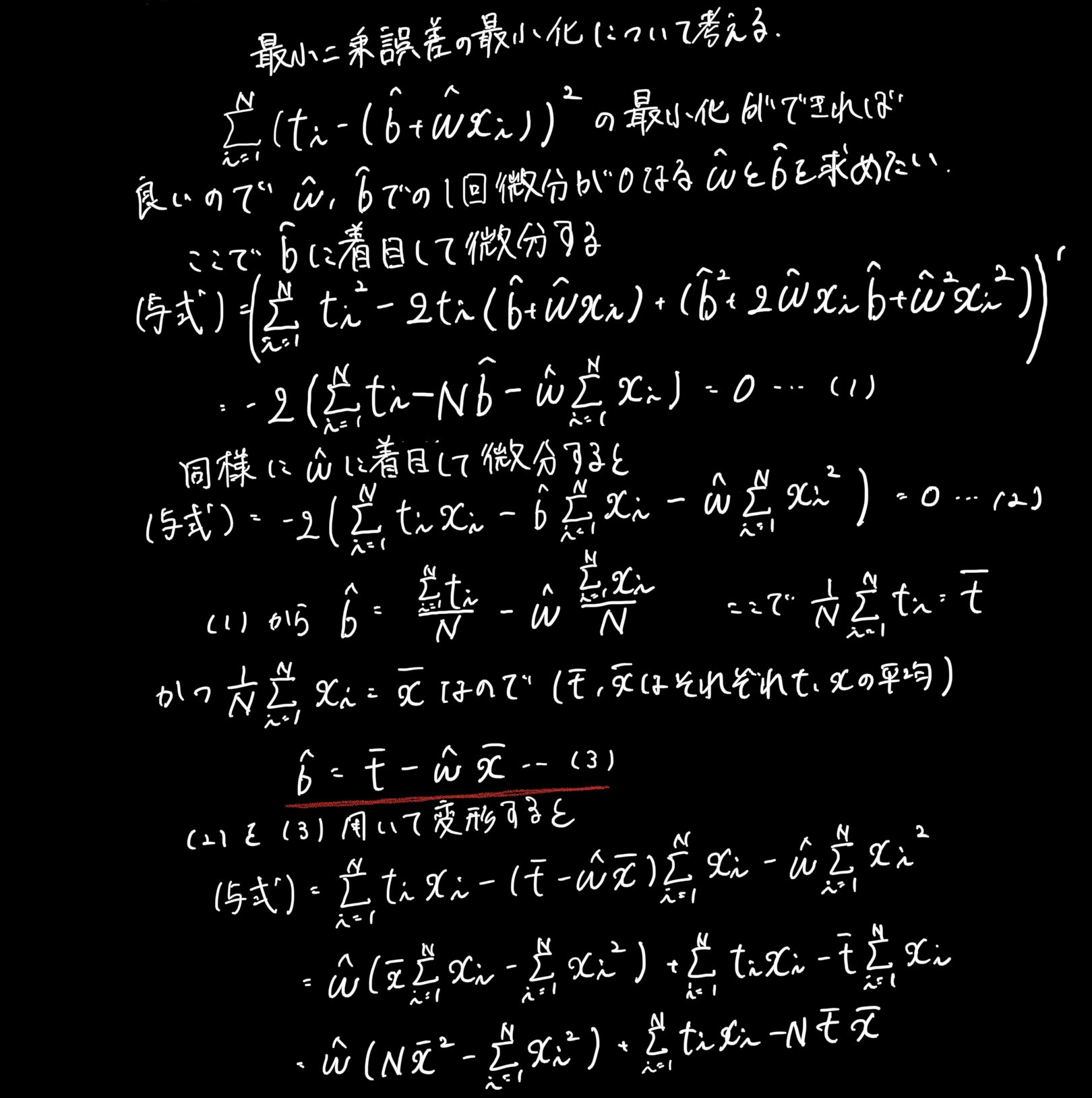
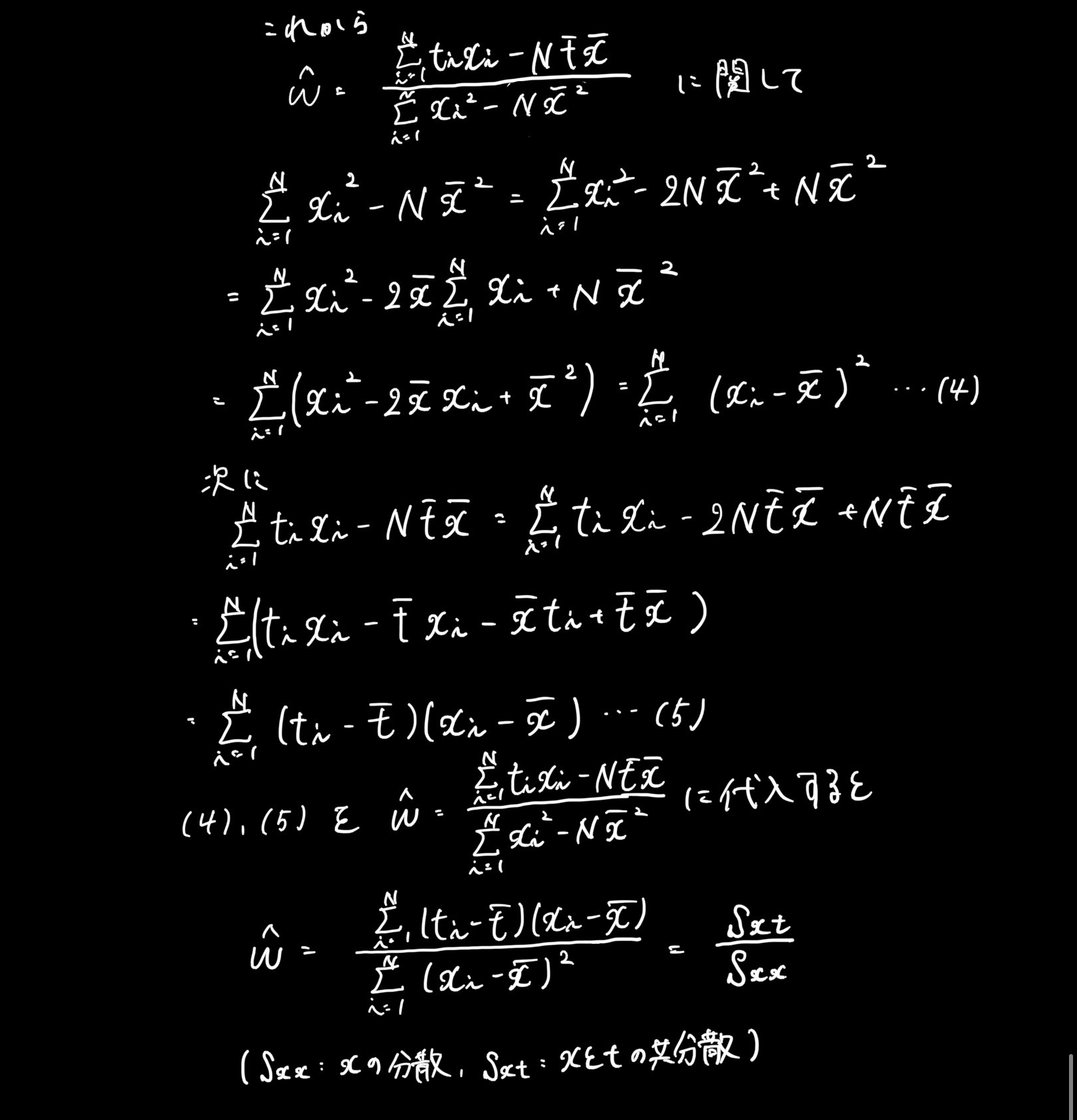
　いやあ、長かった笑
　赤線の部分が前章で触れた回帰係数が標本平均点を通る証明になりますね。
　また、求めたかったb^とw^が求まりましたね。
　これが最小二乗誤差を最小にする値になります。

　最小二乗法の代数的法則

　ここは今までのまとめなんでさっと終わらせようと思います。
　まずは前々章で触れた残差に関する三つの法則です。

　　1.総和が0になること
　　2.説明変数と残差の積和が0になること
　　3.推定値(t_i)と残差が無相関であること

　また、前章において赤線で強調している部分を見てもらうと予測された回帰直線はtとxそれぞれの平均をプロットした点を必ず通ります。この点のことを標本平均点と呼びます。これをまとめると

　　4.予測された回帰直線は標本平均点を通る

　これら4つが大きな代数的法則になります

　さいごに

　今回は単回帰の最小二乗誤差とその最適化について学んでいきました。

　写真で手書きになってしまったところは申し訳ありませんが、なるべく途中式を省かずに書いたつもりです。参考になっていれば幸いです

　次回は重回帰について学んでいこうと思います！！