「数学とコンピュータ2」のAdventCalender22日目です。
https://qiita.com/advent-calendar/2017/math-and-computer2
本記事はベイズ統計初心者が「Think Bayes」というテキストを通してどのようなことを学んだかを記録するためのものです。よってみなさんが思っている高いレベルの内容はかけていないと思います。申し訳ございません。
なので、、、、
「ベイズ統計ってこんな感じに使うんだなぁ、、、と学び始めはこうだった的な昔話をするためのツマミとしてでも活用していただく」もしくは「ベイズの定理を使った推定がどんなものか?の雰囲気をしる」という観点で楽しんでいただければ幸いです。
ベイズの定理について
ベイズの定理の紹介
よくテキストで書かれているベイズの定理は以下の通りです。
事象$A,B$に対して、以下の等式が成り立つ。
$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$
ここで、$P(A|B)$は条件付き確率でこの場合だと「$B$が発生している状態の元での$A$が発生する確率」になり、$P(A|B) = \frac{P(A \cap B)}{P(B)}$と定義されます。
ベイズの定理の別な解釈
この定理の解釈の仕方を少し変えて、仮説$H$と観測されたデータ$D$を使って以下のように解釈します。
仮説$H$と観測されたデータ$D$に対して、以下の等式が成り立つ。
$$ P(H|D) = \frac{P(D|H)P(H)}{P(D)}$$
これはデータが観測された後の仮説が正しい確率は、観測される前に立てた仮説の確率ベースで計算できる、もしくは文献や経験値などで立てた仮説について、その発生確率は観測したデータをベースに最適な確率に更新されていくという風に解釈することもできます。
結論から書いてしまいましたが・・・上記式に出てきている意味について説明していきます。
- $P(H)$は仮説$H$が発生する確率です。この部分はデータ$D$が観測されるされないに関わらない値になります。このことからデータ$D$を観測する前にこちらで主観的に設定できる確率でありこれを事前確率といいます。
- $P(H|D)$はデータ$D$が観測された後に改めて計算された$H$が正しい確率です。これを事後確率と言います。
- $P(D|H)$は尤度といい、「仮説$H$が正しいと仮定した上でデータ$D$が観測される確率」と解釈します。
- $P(D)$は、正規化定数と言います。というのも、、、この$P(D)$はなんの仮定もなしに計算するのは一般的にはものすごく大変なので、起こりうる仮説$H_i$たち(MCMCの条件をみたすもの。データ$D$が発生するための条件を全て網羅。もちろん互いに排反!この$H_i$の中に$H$も入る!)を用いて、
$$P(D) = \sum_i P(D | H_i) P(H_i)$$
と書き換えて計算するからなんです。つまり、コアな計算は1.3.ベースでゴリゴリ計算していき、値が確率して意味のなすように(正確にいうと0-1に収まるように)割り算します。
ベイズ的な考え方での「確率」の計算方法
上記解釈をベースに問題をどうやって解くか
上記解釈をベースに問題をどうやって解くかの手順を以下に示します。
具体例と回答
以下のような問題を考えます。(出典はThinkBayesから。)
M&M's問題
M&M's キャンディでコーティングしたチョコレート菓子で様々な色がついている。
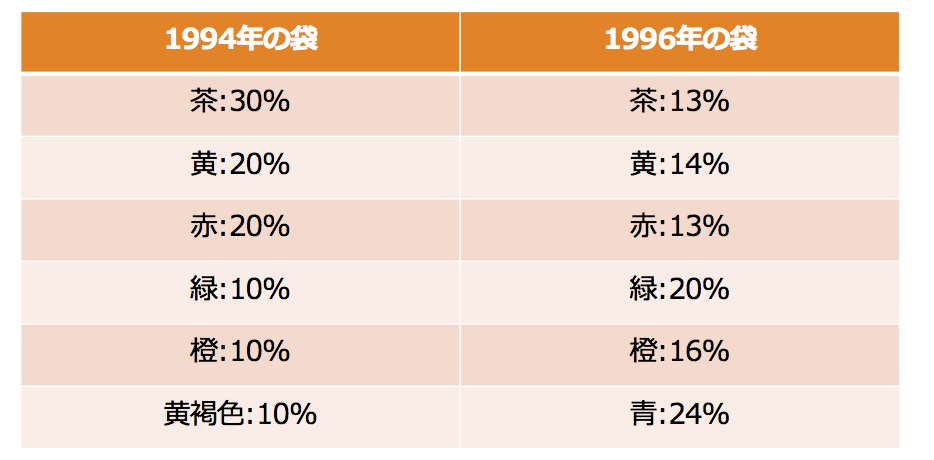
1995年には青いM&M'Sが登場したが、それ以前、普通のM&M'Sの色の取り合わせは30%が茶色、20%が黄色、20%が赤、10%が緑、10%が橙色、10%が黄褐色だった。1995年からは24%が青色、20%が緑色、16%が橙色、14%が黄色、13%が赤色、13%が茶色dった。
友達がM&M'Sの袋を2つ持ってきたとしよう。1つは1994年でもう一つは1996年のもん。どちらかどちらかは教えてくれなかったが、それぞれの袋から1つずつM&M'Sヲクレタ。1つが黄色で、もう一つは緑色だった。聞い色が1994年の袋だという確率はいくらか。
早速、上で挙げた手順でといていきます。
ここで、黄色のM&M'Sを取り出した袋を袋1としそれ以外を袋2とする。
1. 問題を解くのに適した仮説集合を考える。

2. 事前確率を設定する。

情報がない場合に等確率に設定した確率を無情報確率といいます。
3. 尤度を計算する。

それぞれの仮説が成り立つとして、計算する。
4. 5. 事後確率をゴリゴリけいさんする。

ここまでの計算プロセスを見れば、「正規化」するまでの間は各仮説での計算は独立に行われます。「正規化」までの間はベクトル的なイメージでごりごり計算を推し進めることができます。この辺りはRなどのベクトルベースで計算していくプログラムと相性がいいと思われます。
(ここまでくると、ベイズの定理の分母は「最後の確率整合性を保つため」だけというのも頷けます。
ベイズ的な考え方での「値の推定方法」
ここまでは、確率を求めるものだったが、ここでは求めた確率をベースに「値」を推定していきます。
具体的な問題
これもThinkBayesから。
ある鉄道会社は$𝑁$台の機関車を所有しており、機関車に1…𝑁という番号をつけている。
ある日、60番という機関車を目撃した。
このとき、鉄道会社が所有している機関車の台数𝑁を推測せよ。
解き方
これも上記と一緒の手順で解く。ただ、今回の場合確率を求めた後、事後確率ベースの期待値を計算して、これを推定値とする。
手順1.

手順2. 事前確率と尤度を計算。
ここでは事前確率として、過去の機関車数に関する分布の情報をベースとした値を設定します。尤度としては、各番号の車両を出くわすのは等確率を仮定すると計算できます。

手順3.
この情報を元に事後確率と期待値を計算します。
実はこのレベルになると紙ベースでの計算は不可能なので実際はプログラムを組んで計算していきます。
プログラムを組みたかったですが・・・時間がなく断念です。ただ、きちんと値を設定してあげると133-150ぐらいの値がもとまると思います。
プログラムはここをベースに組んで見てください。。。
まとめ
私がThink Bayesというテキストをベースにどんなことを学んだかをつらつらと記載させていただきました。プログラム色は最後の方でしか出なかったですが・・・。
この「値の推定」こそがベイズ統計とかで出てくる「パラメータの推定」で、仮説$H_i$たちの確率が「パラメータが確率分布として捉える」の所以かと思っております。ベイズ統計の資料とか漁るとまず「パラメータ推定」や「パラメータが確率分布で・・・」とか言われることが多いので、このような形でベイズの定理にどのような考え方で問題を解くかをじっくり見ていくとこの辺りの心がわかってくるのではないでしょうか?そして、パラメータ推定をすることでどう応用していくか?なども見えてくれれば嬉しい次第です。
で、計算科学やアルゴリズム、数理的に話題になる「メトロポリタン-ヘイスティング」とか「MCMC」とかというのは、正規化定数を現実的なリソースに納めながら計算していく「近似計算法」なんですよ。。。(問題によっては愚直に計算していくとメモリ不足とかクソみたいに時間がかかるとか解析的に計算不可能とかがある。てかそういうのが多いとかなんとか)
おっと、まとめなのにおしゃべりが過ぎました。。。これを何かの役に立てていただければ幸いです!
参考文献
Think Bayes ―プログラマのためのベイズ統計入門
https://www.amazon.co.jp/dp/4873116945/?tag=hatena_st1-22&ascsubtag=d-lqw93
私が過去に行った自主セミナーでの発表資料
https://www.slideshare.net/LyricalMaestro/vol2-81895119