この記事でやること
GIS系のプログラミングをしている時、しばしば「点と直線の距離問題」に帰着させた処理を実装することがあります。(たとえば、現在地から指定したエリア(多角形で構成されていると仮定)まで距離を計算する、など)平面上の「点と直線の距離問題」であれば中学数学の範囲で楽に計算することができます。
しかし、Geo系の図形問題は、元々の位置を表す値が平面上のものではないので上記公式が使えないです。
この状況下で地球上での「点と直線の距離問題」を解く一つの方法として「平面直角座標系に変換して、その上で解く」という方法があります。しかし、「平面直角座標系の適用範囲は日本だけでも限定的な地域でしか適用できず適用地域横断では、この方法が使えない」という問題があり、異なる座標系に跨がる場合を考慮しないといけないこともあるのでちょっとめんどくさいです。
本記事は、上記問題にぶちあたらない、解法を紹介します。
ざっくり言うと、「地球が真球であることを仮定し、球面幾何学の枠組みで解く」というものです。(これとアプローチ似ているかもしれません…。)
本記事を通してGIS系のプログラミングに関して慣れ親しんでいただければ幸いです。
問題を解く上での仮定
この問題を球面幾何学の枠組みで解くために「地球は「半径 $R$ の球」と仮定する」をします。そして、$R$ は6371kmとして計算します。
この仮定をすることで、
-
2点間の地点を結ぶ「球面上の直線」(数学用語では測地線)は大円の弧として計算できる(この場合の弧の長さを「大円距離」と言います)
-
球面上の三角形の理論が使える
というメリットが生まれます。
問題の定式化
地球上の点と直線の距離問題は以下のように定式化されます。
地球上に引かれた線分p1p2と地点qが与えられた時、p0p1内の点の中でqとの大円距離が最小になる点p0を求めよ。(p0とqの大円距離が「p1p2とqの距離」すなわち「点と直線の距離」である)
- 与えられている情報
- p1, p2, qの緯度経度
- 求めるべき情報
- p0の緯度経度, qとp0の大円距離
計算方法
半径は $R$ としましたが、角度と三角関数中心の議論が肝なので、単位球上で議論をします(最後の本当に地球上の大円距離を出すところだけRが出てくる)
1. 緯度経度の形式から3次元ベクトルの形式に変換
大円の中心角や大円距離をベクトルの内積ベースで出したいので、緯度経度の形式から3次元ベクトル表現に変換します。イメージ的には「球面上だけで見る」というよりも「3次元空間内の点としてみましょう」という感じです。
地球の中心を原点とすれば以下の公式で変換できます。(ただし、以下の lat, lng はそれぞれ緯度経度でdegreeからradianに変換済みのものです)
\begin{align}
x &= \cos (lat) \cos(lng) \\
y &= \cos (lat) \sin(lng) \\
z &= \sin(lat)
\end{align}
2. 大円の中心角の計算
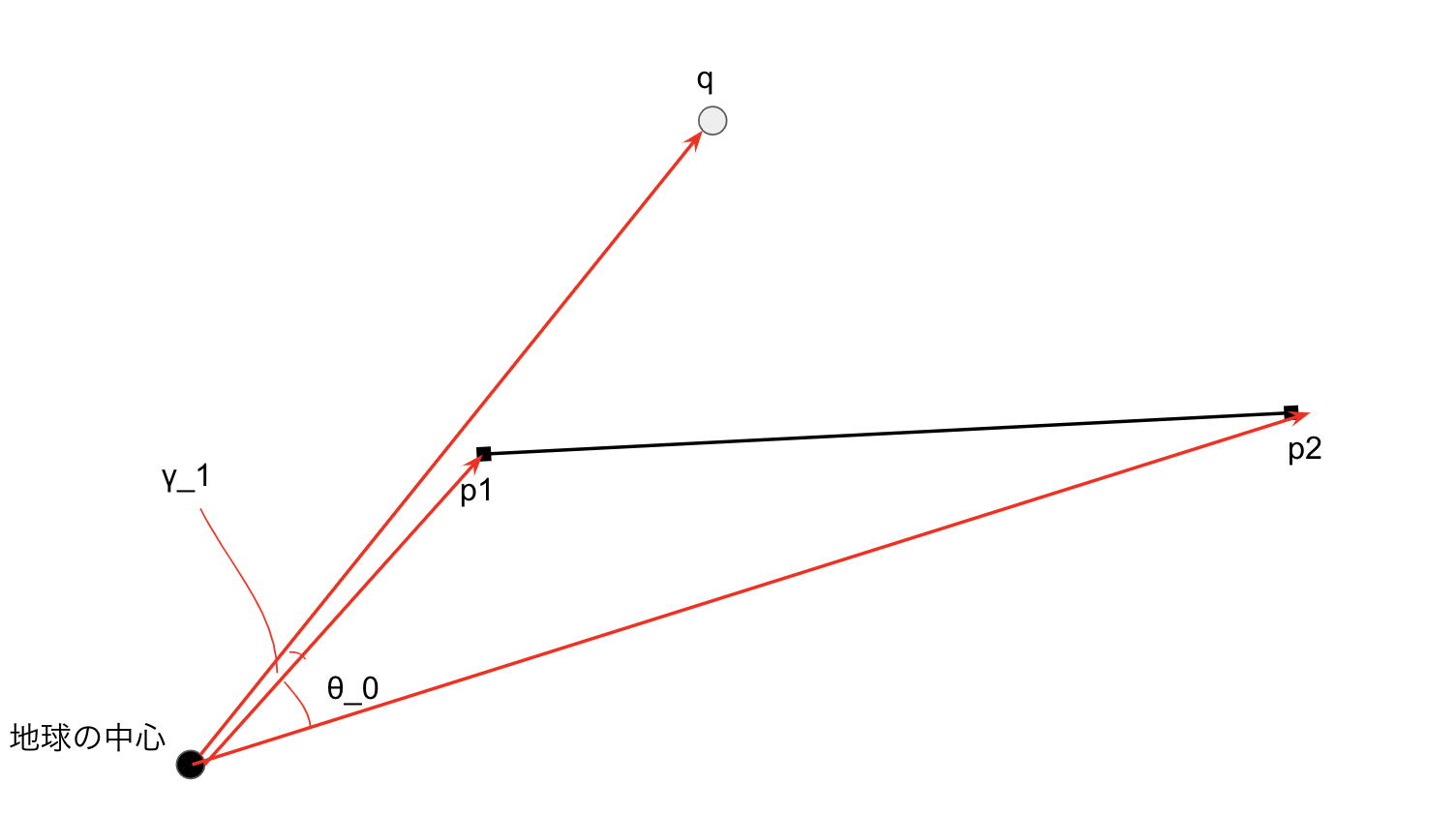
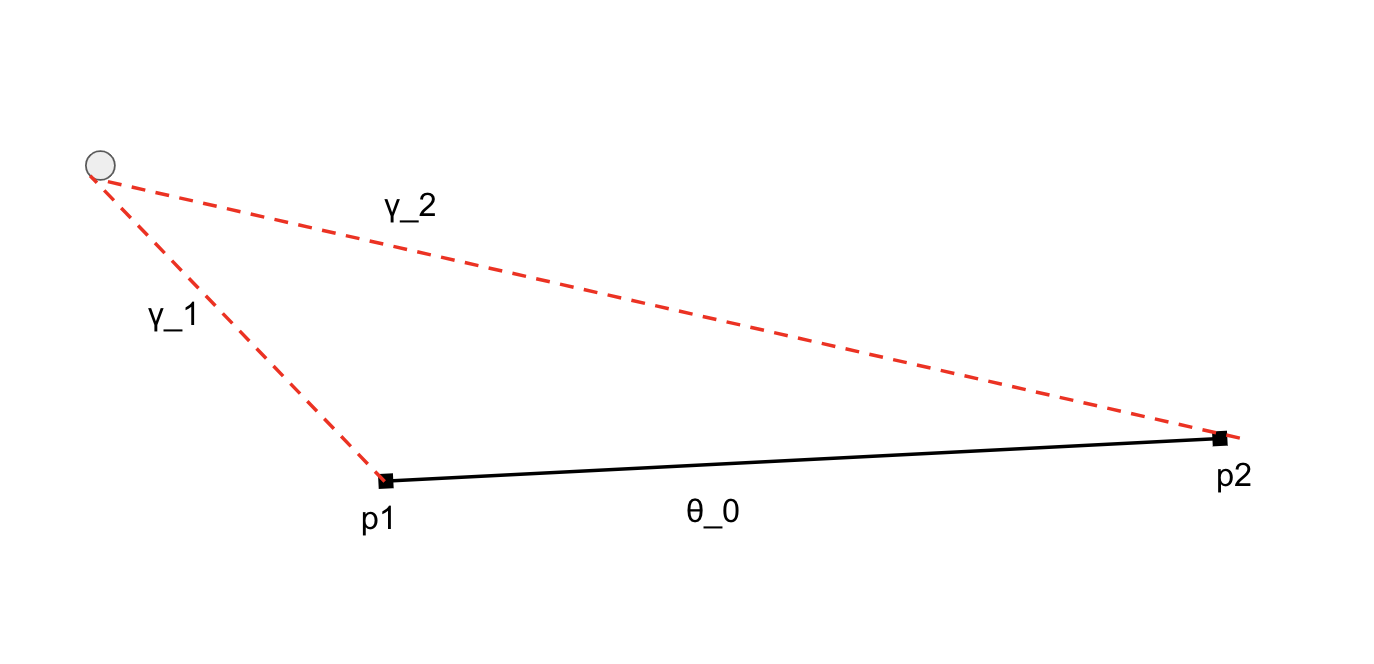
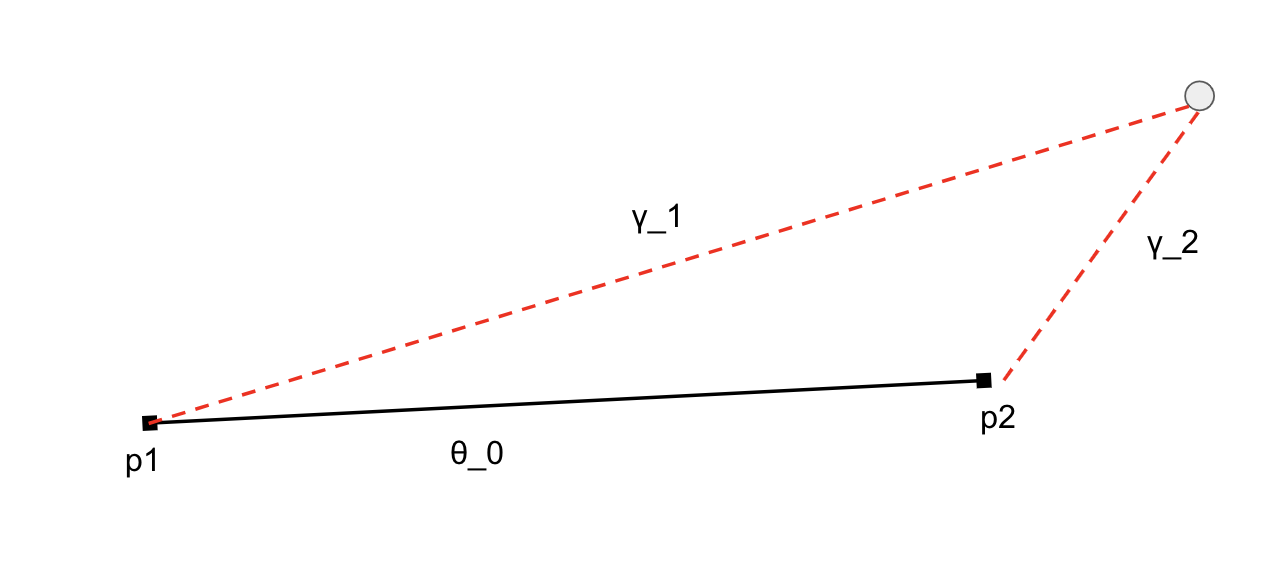
3次元ベクトル表現p_1, p_2 の内積を取り、 $\arccos$ をとると中心角(radian)が計算できます。単位球上あれば中心角がそのまま大円距離になります。
p_1とp_2の中心角を $\theta_0$, p_1とqの中心角を $\gamma_1$、p_2とqの中心角を $\gamma_2$ とします。
3. 球面上の三角形の角A の三角関数を計算し、垂線の中心角(のsin)とp1からp0までの中心角(のcos)の計算
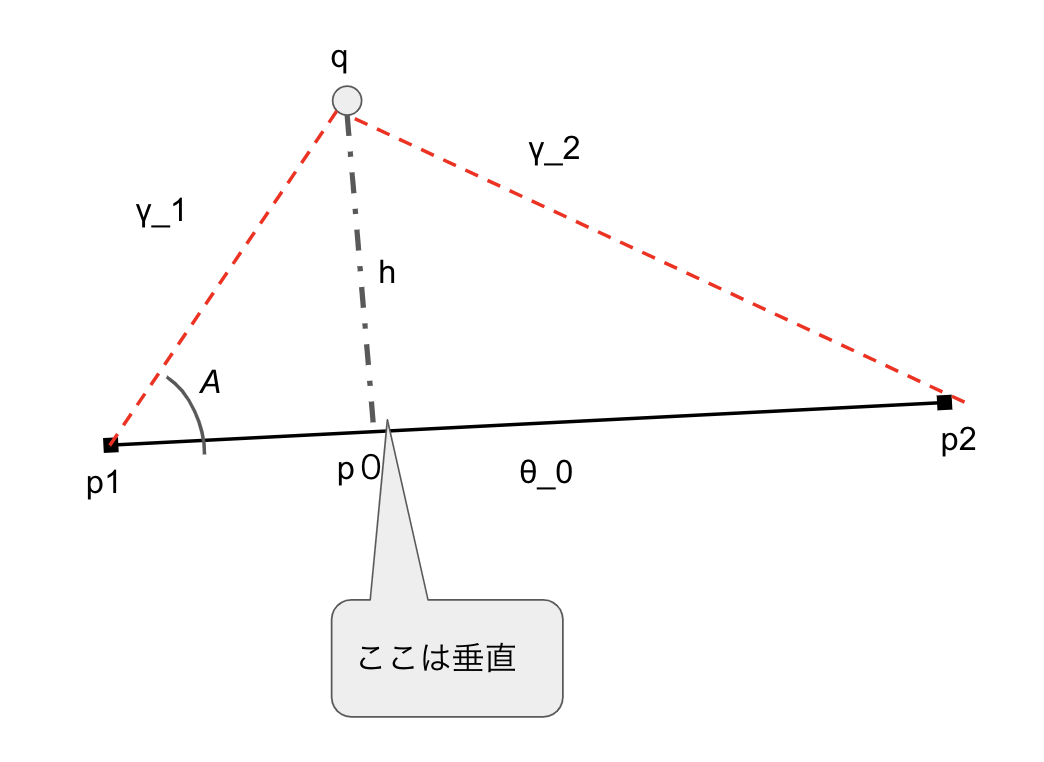
球面三角形p1p2qについて「球面三角形の余弦定理」を使って球面上の三角形の角 $A$ の三角関数を計算します。
角 $A$について球面三角形の余弦定理に当てはめると
\cos\gamma_2 = \cos\theta_0 \cos\gamma_1 + \sin\theta_0 \sin\gamma_1 \cos A
となるので、式変形すると
\cos A = \frac{\cos\gamma_2 - \cos\theta_0 \cos\gamma_1}{\sin\theta_0 \sin\gamma_1}
となる。$\sin A$ は $ 1 = \cos^2 A + \sin^2 A $ から導出できます。(今回は三角形をベースにして考えているので $\sin A \geq 0 $ を仮定しても問題ないです)
また、点と直線の最短で結ぶ線分はその直線と直交するという性質は球面上でも成り立つので、球面三角形p_1p_0qは直角三角形となります。
- 球面上でも「点と直線の最短で結ぶ線分はその直線と直交する」か、はちゃんと証明する必要がありますが、今回は割愛します。アプローチだけさらっとかくと、、、
- (1) 直線上の点p_t と点の3次元空間としての距離で、t上の関数を作る
- (2) (1) をtで微分する。(ベクトルの内積っぽい式が出てくるはず)
- (3) 大円距離が最小になる点が(1)の関数で最小になる点なので、(2)=0となる。この等式はベクトル同士が直交するを意味するので、その辺りをうまくやれば示せます。
球面上の直角三角形のピタゴラスの定理から、qとp_0の中心角$h$(の三角関数)は
\begin{align}
\sin h = \sin\gamma_1 \sin A \\
\end{align}
4. 最短距離を計算
ここで、初めて地球の半径 $R$ が登場します。qとp_0の中心角$h$ をつかって $R*h$ で計算できます。
5. 平面の回転行列の理論を応用して、点p0を計算
5.1. (準備として)p_1, p_0の中心角の計算
p_0を計算するために、p_1, p_0の中心角 $t$ の三角関数を計算します。ここでも球面三角形のピタゴラスの定理を使って、
\cos t = \frac{\cos\gamma_1}{\cos h}
と計算できます。
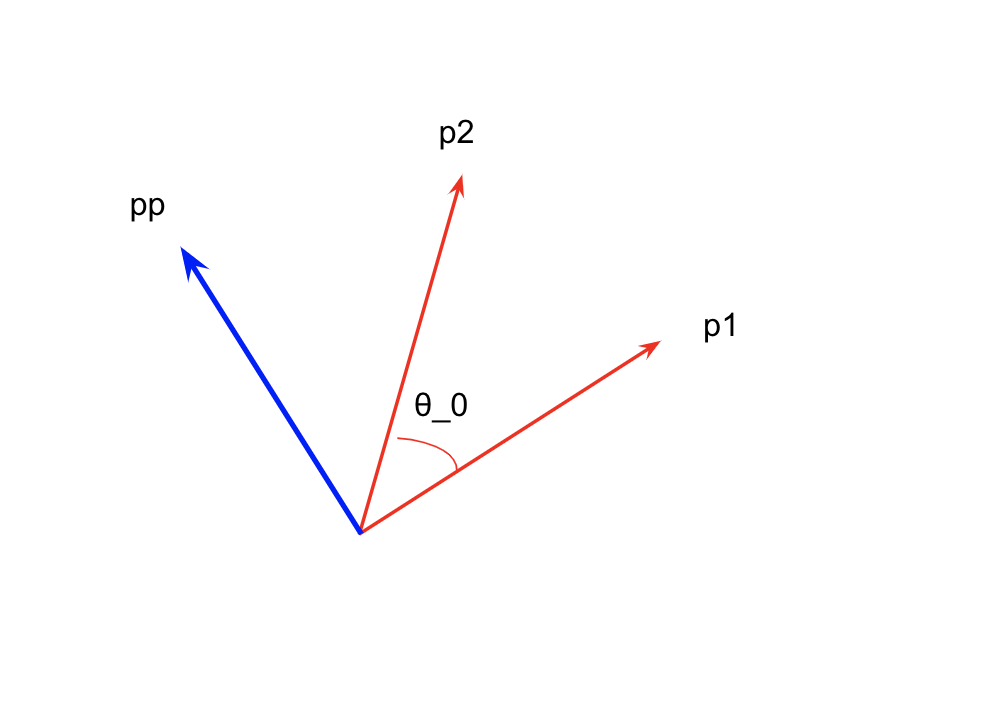
5.2. p_1をx軸とするようなp_1, p_2平面上の回転を計算する。
下図のような座標系(p_1がx軸, ppがy軸)となるような平面で回転の公式を算出したいので、p_1, p_2からppを計算する。
このp_1, ppが計算できれば
p_0 = \cos t * p_1 + \sin t * pp
として、p_0の3次元ベクトル表現が得られます。
p_2 は p_0, pp と中心角 $\theta_0$を使って
p_2 = \cos \theta_0 * p_1 + \sin \theta_0 * pp
と計算できるので、ここから
pp = \frac{p_2 - \cos \theta_0 * p_1}{\sin \theta_0}
と計算できます。
5.3. 3次元ベクトル表現p_0から緯度経度の形式に変換
- で示した等式から算出します。等式を使っただけだとラジアン形式なのでdegree形式に戻しておいたほうが親切です。
プログラム
上記方法で計算するpythonコードを以下に示します。
# coding: UTF-8
import dataclasses
import math
from typing import Tuple
import numpy as np
from nptyping import NDArray
# (x, y, z)座標
Vector = NDArray[3, float]
# ((経度, 緯度), (経度, 緯度)) の並び
Line = Tuple[Tuple[float, float], Tuple[float, float]]
@dataclasses.dataclass
class Result:
lng : float # snap点の経度
lat : float # snap点の緯度
distance : float # 入力点とsnap点との大円距離(単位はm)
class Snapper:
# 地球の半径(単位はm)
R = 6371 * 1000.0
def __init__(self):
pass
def _to_vector_tuple(self, lng: float, lat: float) -> Vector:
rlng = math.radians(lng)
rlat = math.radians(lat)
x = math.cos(rlat) * math.cos(rlng)
y = math.cos(rlat) * math.sin(rlng)
z = math.sin(rlat)
return np.array([x, y, z])
def _calc_center_angle(self, vec1: Vector, vec2: Vector) -> float:
return math.acos(np.dot(vec1, vec2))
def snap(self, line_segment:Line, lng: float, lat: float):
from_p = line_segment[0]
to_p = line_segment[1]
# こうすることで、p0_x <= p1_x の状態を作り出す
if from_p[0] > to_p[0]:
tmp = from_p
from_p = to_p
to_p = tmp
# 3次元空間への埋め込み
p1 = self._to_vector_tuple(lng=from_p[0], lat=from_p[1])
p2 = self._to_vector_tuple(lng=to_p[0], lat=to_p[1])
q = self._to_vector_tuple(lng=lng, lat=lat)
# 大円の中心角計算
theta_0 = self._calc_center_angle(p1, p2)
gamma_1 = self._calc_center_angle(p1, q)
gamma_2 = self._calc_center_angle(p2, q)
## 垂線の中心角(のsin)とp1からsnap点までの中心角(のcos)の計算
cos_a = (math.cos(gamma_2) - math.cos(theta_0) * math.cos(gamma_1)) / (math.sin(theta_0) * math.sin(gamma_1))
sin_a = math.sqrt(1 - cos_a ** 2)
sin_h = math.sin(gamma_1) * sin_a
cos_t1 = math.cos(gamma_1) / (math.sqrt(1 - sin_h ** 2))
if cos_t1 <= math.cos(theta_0):
# snap点が計算上線分の外に出てしまう場合
dist = gamma_2 * self.R
lng = to_p[0]
lat = to_p[1]
elif 0 >= cos_a:
# snap点が計算上線分の外に出てしまう場合
dist = gamma_1 * self.R
lng = from_p[0]
lat = from_p[1]
else:
# 垂線の距離計算
dist = math.asin(sin_h) * self.R
## snap点の計算用のp1, p2 平面の p1軸と垂直なpp軸の計算
pp = (p2 - math.cos(theta_0) * p1) / math.sin(theta_0)
pp = pp / np.sqrt(np.dot(pp, pp))
## snap点計算
theta = math.acos(cos_t1)
p0 = math.cos(theta) * p1 + math.sin(theta) * pp
lat = math.asin(p0[2])
lng = math.acos(p0[0] / math.cos(lat))
lat = math.degrees(lat)
lng = math.degrees(lng)
return Result(lng=lng, lat=lat, distance=dist)
if __name__ == '__main__':
line = ((140.0713759,35.6597144), (140.078929,35.6599934))
q = (140.07723, 35.66098)
result = Snapper().snap(line, q[0], q[1])
print("input : ")
print(f" line = {line}")
print(f" q = {q}")
print("output : ")
print(f" {result}")
if文で分岐している箇所の解説
本編の計算ロジックでは解説していない以下の二つについて対応したものです。
- (1) qがp_1よりずっと西にある場合
- (2) qがp_2よりずっと東にある場合
どちらも「直線」p_1p_2上には垂線がひけるが、p_0が線分上に乗らないケースです。この場合は最短距離とその点p_0はそれぞれ (1) p_1, $\gamma_1$ (2) p_2, $\gamma_2$ となります。
判定条件の意図については以下の通りです。
- (1) のケースだと $A$が鈍角になります。$A$が鈍角か否か、を $\cos$の言葉で表現しています。
- (2) のケースだと p_1p_0の中心角はp_1p_2よりも大きくなります。中心核の比較を $\cos$の言葉で表現しています。( $\cos$ は三角形の角度の範囲だと単調減少なので角度のままの比較のときと逆の不等号になります)
(1)
(2)
実際の計算結果
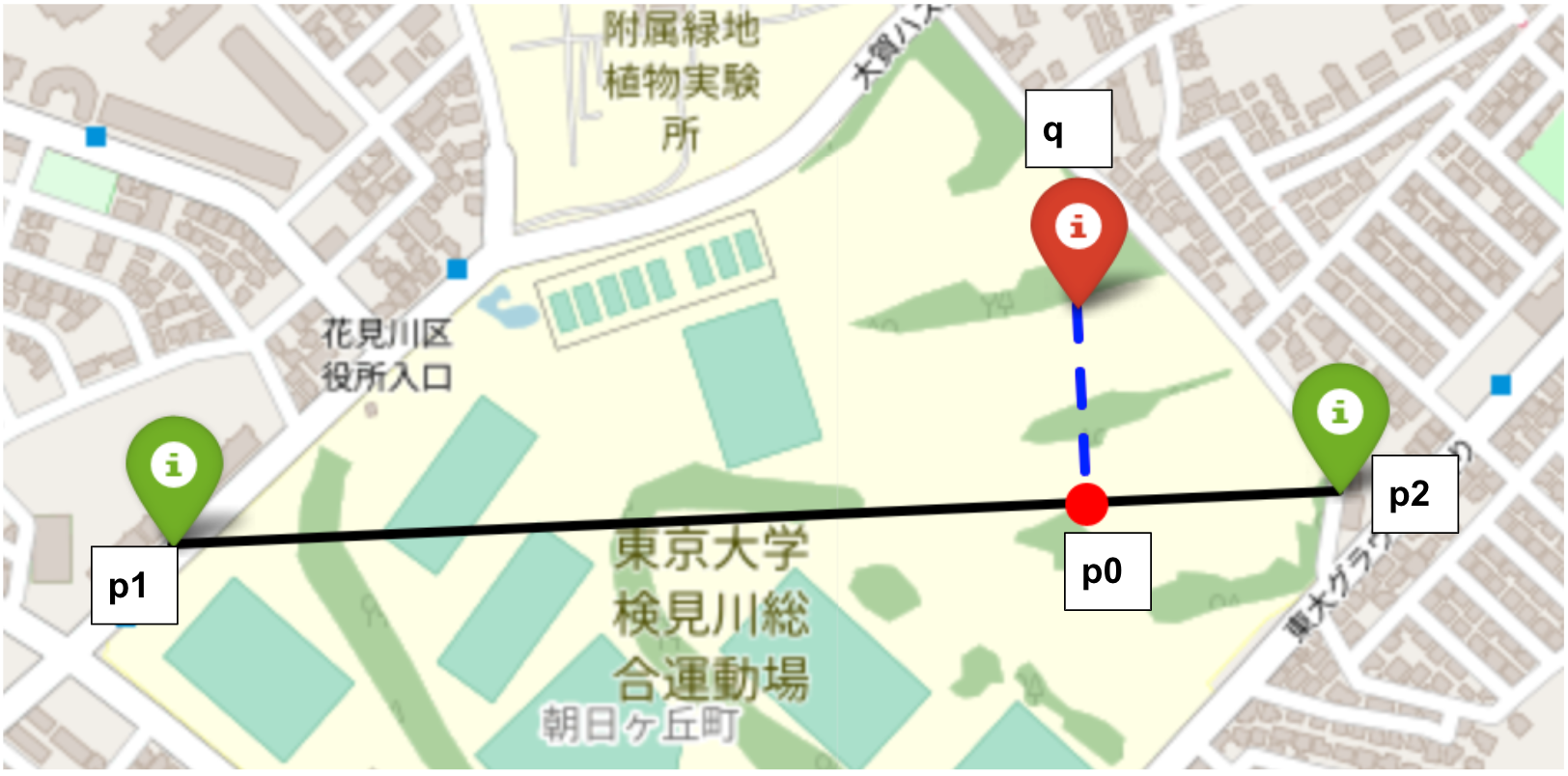
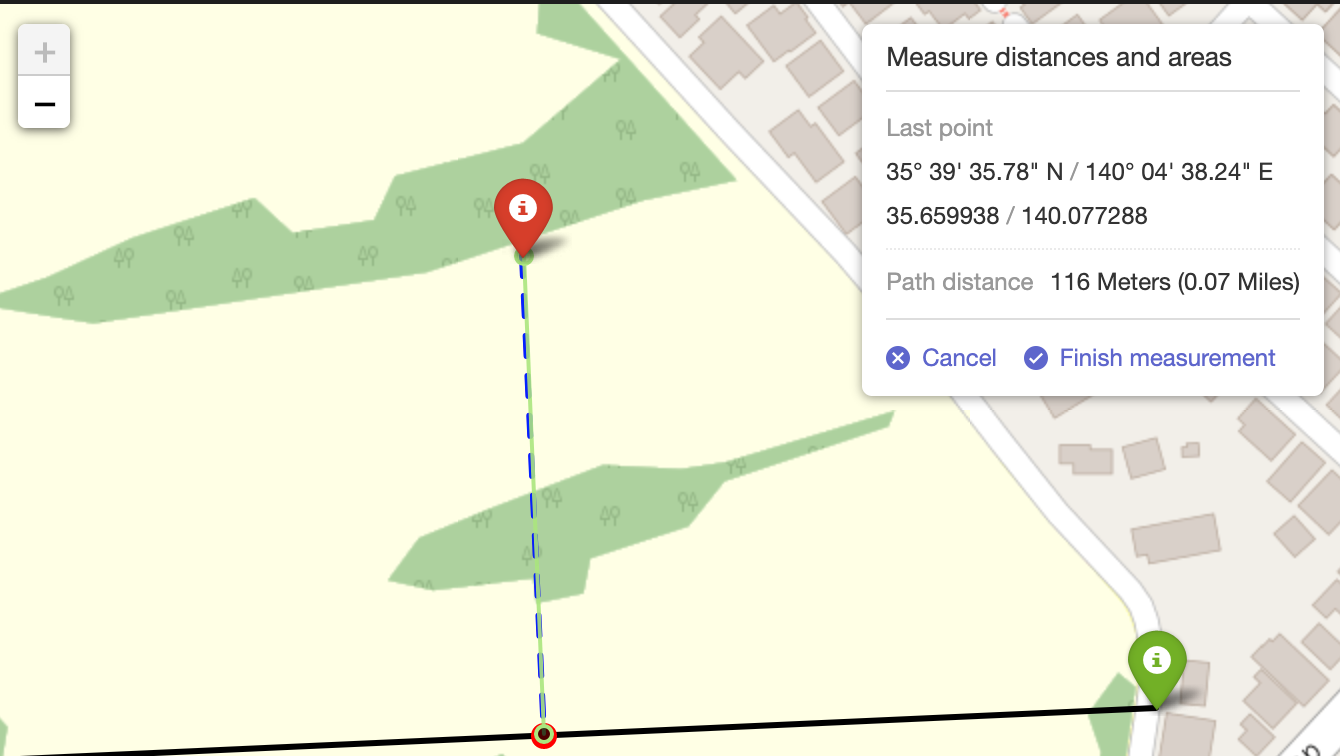
上記プログラムを実行すると以下のような計算結果が得られます。
また、問題の点と線分、そしてp_0をfoliumを使って描画してみると「平面上で点と直線の距離問題を考えた時と同じような」結果が得られます。
foliumのMeasure機能(面積や距離を地図上の操作で計測できる)を使って測ってみると、116mで計算結果と大きなズレはないです。
まとめ
XY座標変換しなくても地球上の「点と直線の距離問題」は解けます!
ただし、どちらが精度がいいか、どちらが計算速度が速いか、みたいな検証はしていないので興味がある方は試してみてください。
参考文献
-
球面三角形の定理 高校生に向けて
- http://horibe.jp/PDFBOX/SphericalTriangles.pdf
- 球面三角形の余弦定理・ピタゴラスの定理を計算している
-
点と直線の距離の公式
-
地球上の点と線分の距離
-
wikipedia「大円距離」