はじめに
カジュアルにパズルを楽しめるスマホアプリの1つにLightsOutがあります。LightsOutはシンプルなゲームながら面白い数学を使った話が隠れています。
この記事では、
- LightsOutはどんなゲームか、どの部分を数学の問題に落とし込むか
- 落とし込んで何がわかるか?
を紹介していきます。身近なゲームに潜んでいる数学の面白さを感じていただけたら幸いです。
前提知識
- 線形代数。と言っても行列と一次連立方程式の関係とジョルダンの掃き出し法とかまで。
- 剰余環の初歩。と言っても2を法にした数字同士の四則演算とか知って入ればOK.
http://hooktail.sub.jp/algebra/Characteristic/ とかは骨があるけどしっかり開設されています。
LightsOutとは?
正方形状に並べた$n^2$個のライトがあります。
それぞれのライトはON(下の図でいうと赤)、OFF(下の図で言うと灰色)の二つの状態を持ちます。

プレイヤーはライトをタップしてライトのON/OFFを切り替えることができます。しかし、切り替わるのはタップしたライトだけでなう4方向に隣り合うライトのON/OFFも切り替わります。
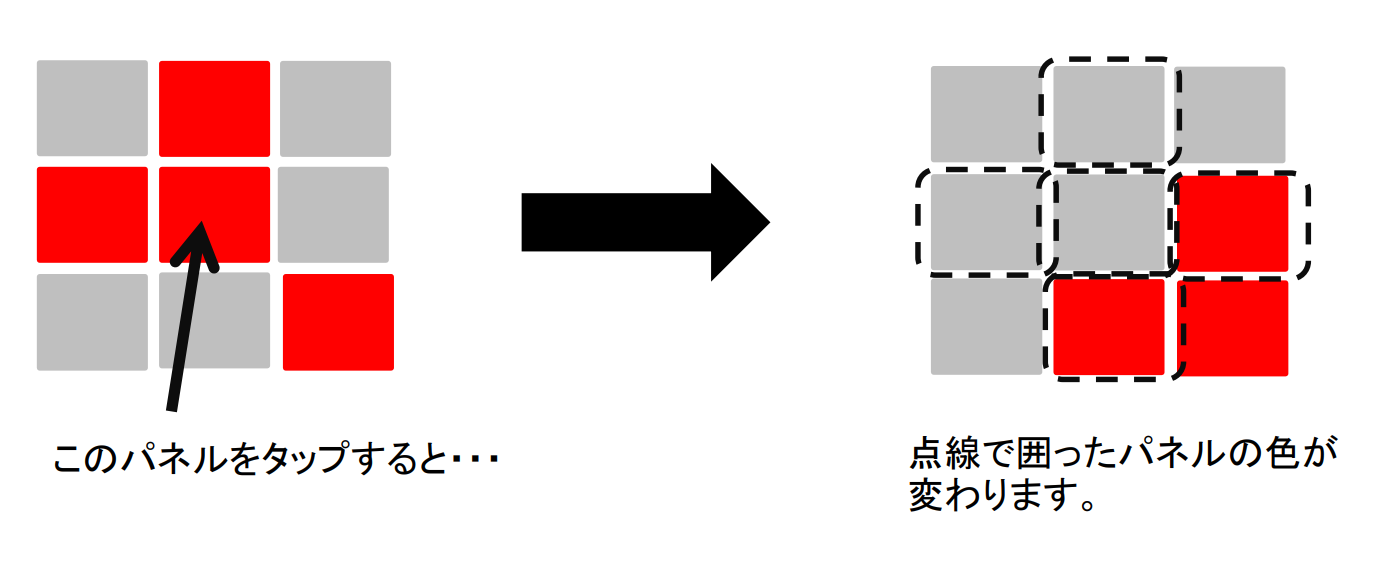
何回かライトをタップしていって全てのライトをOFFにしていくゲームです。

正方形状に並べた$n^2$個のライトのことを(数学的に定式化しやすいように)LightsOutといいます。
ゲーム自体はここからDLできます。
https://play.google.com/store/apps/details?id=com.lyricaloriginal.beginnerslightsout2&hl=ja
LightsOutを解くとは?
何回かタップしていくと$n^2$個のライトはOFFにできます。たとえば、タップするライトを間違えたと言う時はもう一度間違えてタップしたライトをタップすればundoみたいなことができます。
では、与えられた$n^2$個のライトは最低何回タップすればOFFにできるでしょうか。それはどのライトをどの順番でタップすればOKでしょうか。
与えられた$n^2$個に対する回答を用意することをLightsOutの解を見つけると言うふうに言います。
LightsOutを線形代数の世界に落とし込んで解く。
最初の一歩
- $n^2$個のライツアウトの各ライトのON/OFFの状態は、$n^2$次ベクトルを使って表現できます。各要素には「ONのときは$1$, OFFのときは$0$」が入ります。

以下の$3 \times 3$個のライツアウトの場合は以下の図のように定式化されます。

\begin{pmatrix}
1\\
0\\
0\\
1\\
1\\
1\\
1\\
0\\
0
\end{pmatrix}\hspace{8cm}
- $(i,j)$番めのライトをタップした時のON/OFFの変化もベクトルを用いて以下のように表現されます。
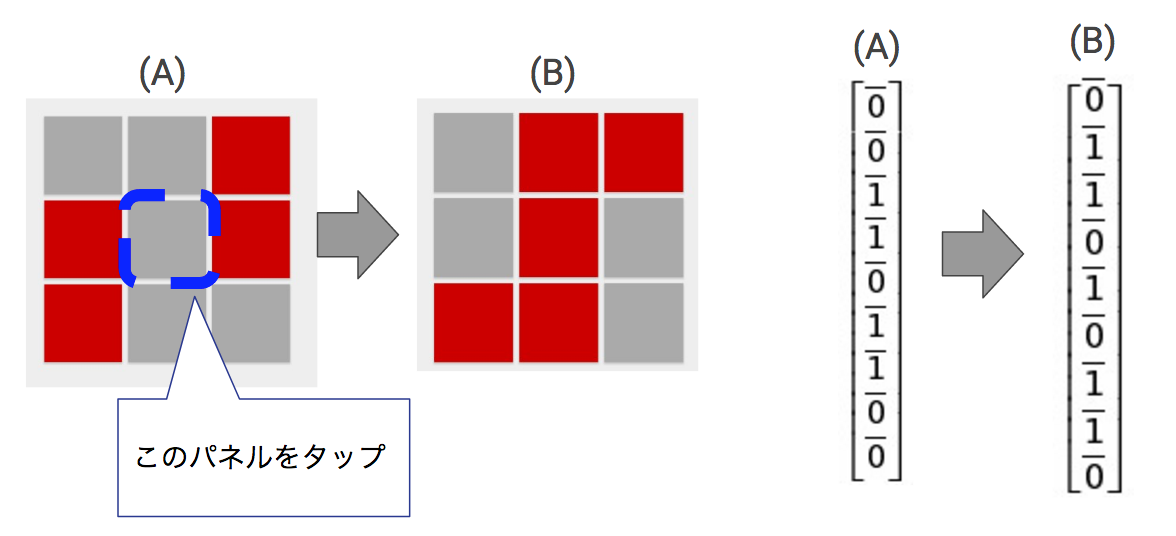
この対応のままだと数学的な対応が難しいので、以下のようにします。
2を法にした数の概念を使う。
先ほどの1.で定式化した時に使った数字を通常の$0$, $1$でなく2を法にした数(標数2の体)を用います。これらを $\bar{0}$, $\bar{1}$と記述します。この数はもちろん四則演算が定義され、足し算・かけ算は以下のようになります。
\bar{0} + \bar{0} = \bar{0},\hspace{2cm} \bar{0} + \bar{1} = \bar{1}\\
\bar{1} + \bar{0} = \bar{1},\hspace{2cm} \bar{1} + \bar{1} = \bar{0}\\
\bar{0} \times \bar{0} = \bar{0},\hspace{2cm} \bar{0} \times \bar{1} = \bar{0}\\
\bar{1} \times \bar{0} = \bar{0},\hspace{2cm} \bar{1} \times \bar{1} = \bar{1}\\
当然、分配法則、結合補足、足し算についての交換法則が成り立つ。
この数を要素にしたベクトルについても足し算・スカラー倍は通常の場合と同様に、各成分の足し算・スカラー倍として定義されます。
\begin{pmatrix}
\bar{x_{1}}\\
\bar{x_{2}}\\
\vdots \\
\bar{x_{n}}\\
\end{pmatrix}
+
\begin{pmatrix}
\bar{y_{1}}\\
\bar{y_{2}}\\
\vdots \\
\bar{y_{n}}\\
\end{pmatrix}
=
\begin{pmatrix}
\bar{x_{1}} + \bar{y_{1}}\\
\bar{x_{2}} + \bar{y_{2}}\\
\vdots \\
\bar{x_{n}} + \bar{y_{n}}\\
\end{pmatrix},
\hspace{0.5cm}
\bar{c}
\begin{pmatrix}
\bar{x_{1}}\\
\bar{x_{2}}\\
\vdots \\
\bar{x_{n}}\\
\end{pmatrix}
=
\begin{pmatrix}
\bar{c} \times\bar{y_{1}}\\
\bar{c} \times\bar{y_{2}}\\
\vdots \\
\bar{c} \times\bar{y_{n}}\\
\end{pmatrix}
- の「$(i,j)$番めのライトをタップした時のON/OFFの変化」も足し算を用いて表すことができます。
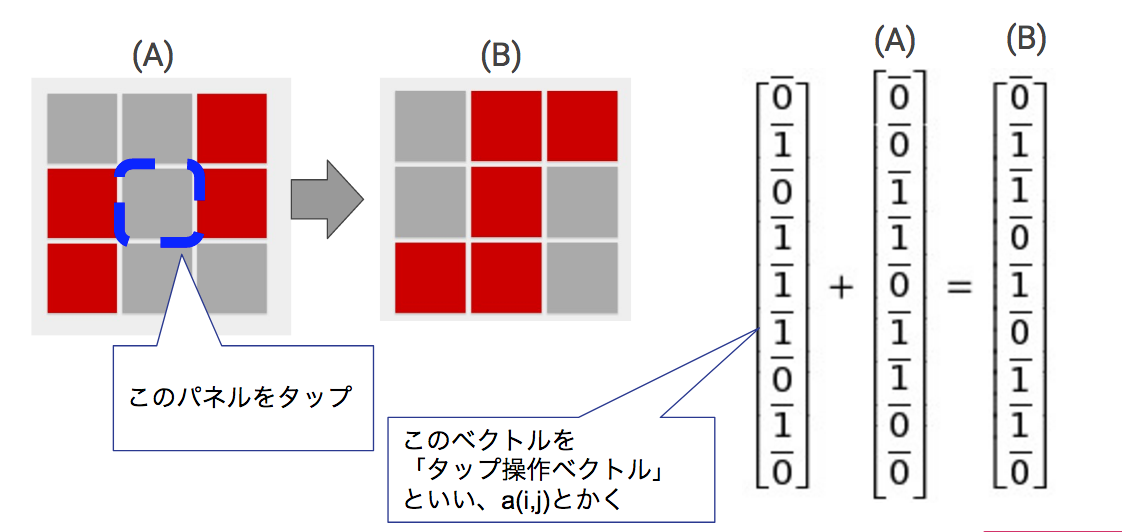
この定式化から以下のことが言えます。
- タップの順番は入れ替えても同じ。
$(i,j)$番めをタップした時に足されるベクトル$a(i,j)$と$(i,j)$をタップしたか否かを表す$\bar{x_{i,j}}$(標数2の体の元です)、そして、全てOFFはベクトルの要素が全て$\bar{0}$であることと同値なので
与えられたLightsOut(ベクトルで$(\bar{b_{i,j}})$とかく)の最小のタップ数と手順を求めるには$\bar{x_{i,j}}$についての方程式をとけばよいことになります。
\sum_{1\leq i,j \leq n} \bar{x_{i,j}} a(i,j)
+
\begin{pmatrix}
\bar{b_{1,1}}\\
\bar{b_{1,1}}\\
\vdots \\
\bar{b_{1,n}}\\
\bar{b_{2,1}}\\
\vdots \\
\bar{b_{n,n}}\\
\end{pmatrix}
=
\begin{pmatrix}
\bar{0}\\
\bar{0}\\
\vdots \\
\bar{0}\\
\end{pmatrix}
\hspace{3cm}(1)
これは行列を用いると以下のように書き換えることができる。(2を法にした数を成分とした行列とベクトルの積は通常の行列とベクトルの席と同様に定義される)
\begin{pmatrix}
\\
\\
\\
a_{1,1} & a_{1,2} & \cdots & a_{1,n} & a_{2,1} & \cdots & a_{n,n} \\
\\
\\
\\
\end{pmatrix}
\begin{pmatrix}
\bar{x_{1,1}}\\
\bar{x_{1,2}}\\
\vdots \\
\bar{x_{1,n}}\\
\bar{x_{2,1}}\\
\vdots \\
\bar{x_{n,n}}\\
\end{pmatrix}
=
\begin{pmatrix}
\bar{b_{1,1}}\\
\bar{b_{1,1}}\\
\vdots \\
\bar{b_{1,n}}\\
\bar{b_{2,1}}\\
\vdots \\
\bar{b_{n,n}}\\
\end{pmatrix}
[上記の言い換えが成り立つ証明]
(1)の両辺にまず$(\bar{b_{i,j}})$を足すと、
\sum_{1\leq i,j \leq n} \bar{x_{i,j}} a(i,j)
=
\begin{pmatrix}
\bar{b_{1,1}}\\
\bar{b_{1,1}}\\
\vdots \\
\bar{b_{1,n}}\\
\bar{b_{2,1}}\\
\vdots \\
\bar{b_{n,n}}\\
\end{pmatrix}
\hspace{3cm}(2)
この後以下のように変形していけばOK
\begin{align}
(2)の左辺 &=
\sum_{1\leq i,j \leq n} \bar{x_{i,j}}a(i,j)
\\
&=
\sum_{1\leq i,j \leq n}
\begin{pmatrix}
\bar{x_{i,j}} a(i,j)_{1}\\
\bar{x_{i,j}} a(i,j)_{2}\\
\vdots \\
\bar{x_{i,j}} a(i,j)_{n^{2}}\\
\end{pmatrix}
\\
&=
\begin{pmatrix}
\sum_{1\leq i,j \leq n}\bar{x_{i,j}} a(i,j)_{1}\\
\sum_{1\leq i,j \leq n}\bar{x_{i,j}} a(i,j)_{2}\\
\vdots \\
\sum_{1\leq i,j \leq n}\bar{x_{i,j}} a(i,j)_{n^{2}}\\
\end{pmatrix}
\\
&=
\begin{pmatrix}
\\
\\
\\
a_{1,1} & a_{1,2} & \cdots & a_{1,n} & a_{2,1} & \cdots & a_{n,n} \\
\\
\\
\\
\end{pmatrix}
\begin{pmatrix}
\bar{x_{1,1}}\\
\bar{x_{1,2}}\\
\vdots \\
\bar{x_{1,n}}\\
\bar{x_{2,1}}\\
\vdots \\
\bar{x_{n,n}}\\
\end{pmatrix}
\end{align}
実際に例をみてみましょう。以下の$3\times3$のライツアウトだと定式化は右のようになります。

実際この連立方程式をとくと以下の左のベクトルのようになります。これは右図の「紫の四角で囲まれたライト」をタップすれば最短のタップ数でクリアできることを意味しています。

Solverあります。
これを具体的に実装したJavaプログラムを作りました。適当に遊んでみてください。
https://github.com/LyricalMaestro/LightsOutSolver
ライツアウトを線形代数の世界に落とし込んでわかること。
- $3\times3$個, $6\times6$個の場合はどんなライトのON/OFFの状態でも必ず解ける。しかも、その手順は一意に定まる。
- $4\times4$個, $5\times5$個の場合は解けない場合がある。解けたとしてもその手順が一通りとは限らない。
これらの性質は連立方程式からでてくる行列が正則かどうかによってわかります。正則でない場合は、連立方程式の解となりうるパターンはいくつか存在します。実際、最小のタップ数となる手順を求める時には
- 連立方程式の解の一つを求める。
- 行列に対応する核に属するベクトル(有限個)分、1.で求めた解と足したものを出す。
- 2.ででてきたベクトルの中で$\bar{1}$の数が最小のものをとってくる。
という手順を踏みます。
まとめ
一見数学が関与しなさそうなパズルゲームでも線形代数の概念を導入すれば自動で解き方を導き出してくれるプログラムを作るコアな考えを提供してくれます。
これをきにもう一度線形代数を勉強して、実務で抱えている問題を解決するのに役立ててみてはいかがでしょう。