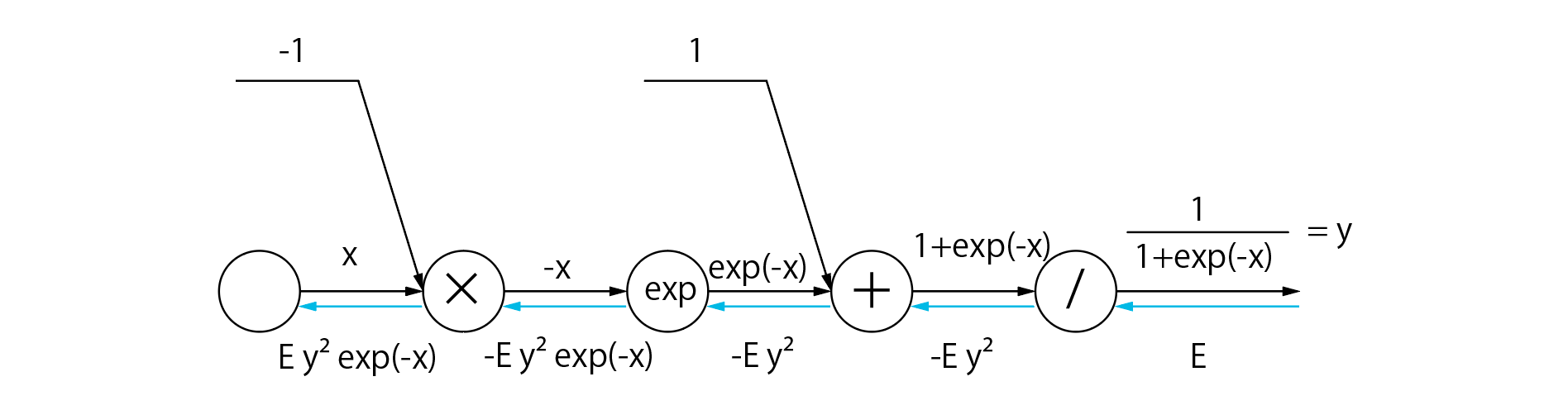C++で作るDeepLearning - パート3

目次

1. C++で作るDeepLearning - パート1
2. C++で作るDeepLearning - パート2
3. C++で作るDeepLearning - パート3　←今回

パート1~3を全て実装したコードはGitHubにあります。(多少コードが違ってるかも)

このパートでは、学習の効率化のための、「誤差逆伝播法」について解説・実装していきます
※簡単な微分ができると読みやすいと思います

計算グラフ

順伝播

誤差逆伝播法の解説のために、まず計算グラフというものについて解説しておきます。

計算グラフは、簡単にいうと「計算の過程を図に表したもの」です。
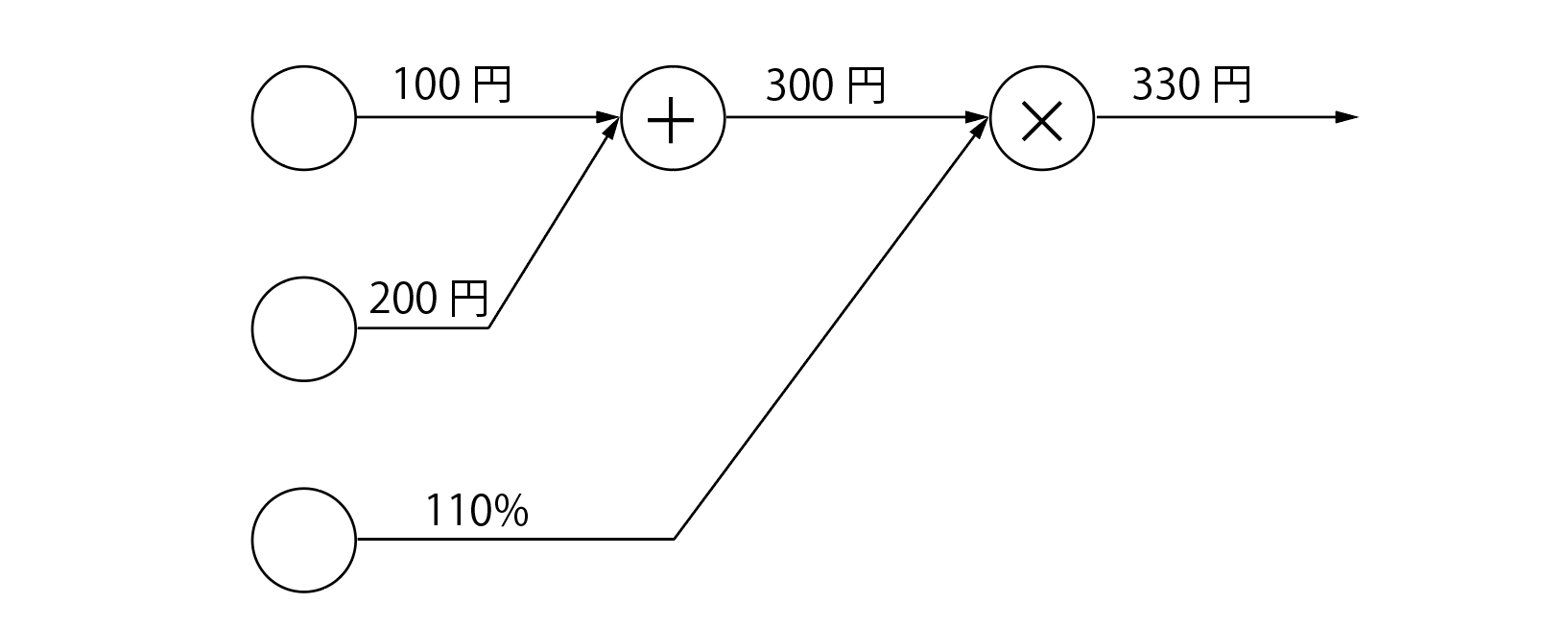
例えば、「100円のリンゴと200円のみかんを消費税10%で買う」とき、この計算グラフはこんな感じになります。

まず、りんごの100円とみかんの200円を「＋」というノードで足し合わせ(300円)、その後その値を消費税の110%と「×」ノードで掛け合わせて最終的に合計金額は330円となりました。このような、計算グラフ乗を始点から終点まで向かうことを「順伝播」と呼びます

逆伝播

では、次に「各値を少し変えると最終的な値にどう影響するか」という問題を考えてみましょう。
ぱっと思いつくのは、パート2の数値微分のように、それぞれの値を微少量だけ変えて計算してみる、というやり方です。それも正解です。

ですが、計算グラフの場合、「逆伝播」という手法を使えば、より少ない計算回数でこの問題を解くことができます。
逆伝播は、その名の通り、計算グラフを終点から始点へと辿っていきます。ただ、たどり方が順伝播とは違って、「そのノードの局所的な微分を掛ける」ことを繰り返します。

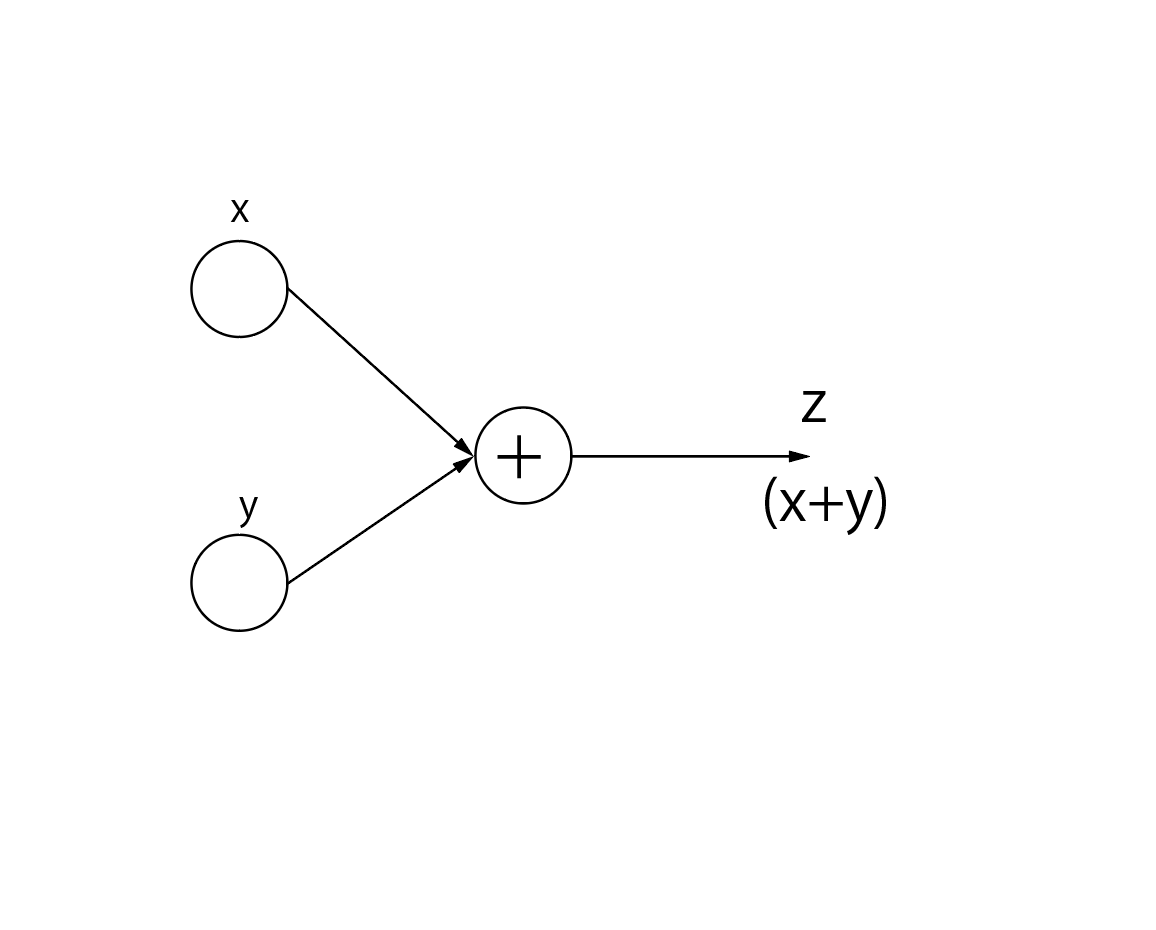
例えば、「＋」のノードの場合、計算グラフと表す式は下のようになります。

z=x+y

そして、この式の(偏)微分は、

• xについて：$\frac{dz}{dx}=1$
• yについて：$\frac{dz}{dy}=1$

なので、「＋」ノードの逆伝播は受け取った値をそのまま渡すことになります。

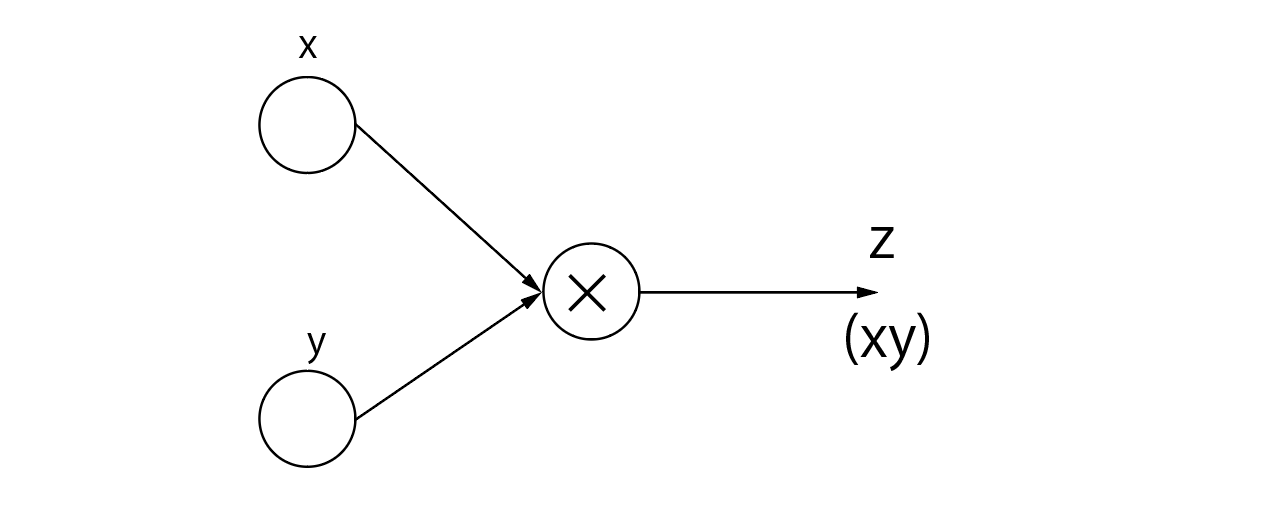
もう一つ、「×」ノードについても考えてみましょう。グラフと式は下のようになります。

z=xy

これも(偏)微分すると、

• xについて：$\frac{dz}{dx}=y$
• yについて：$\frac{dz}{dy}=x$

なので、「×」ノードについての微分は計算グラフをそのまま逆走することになります。

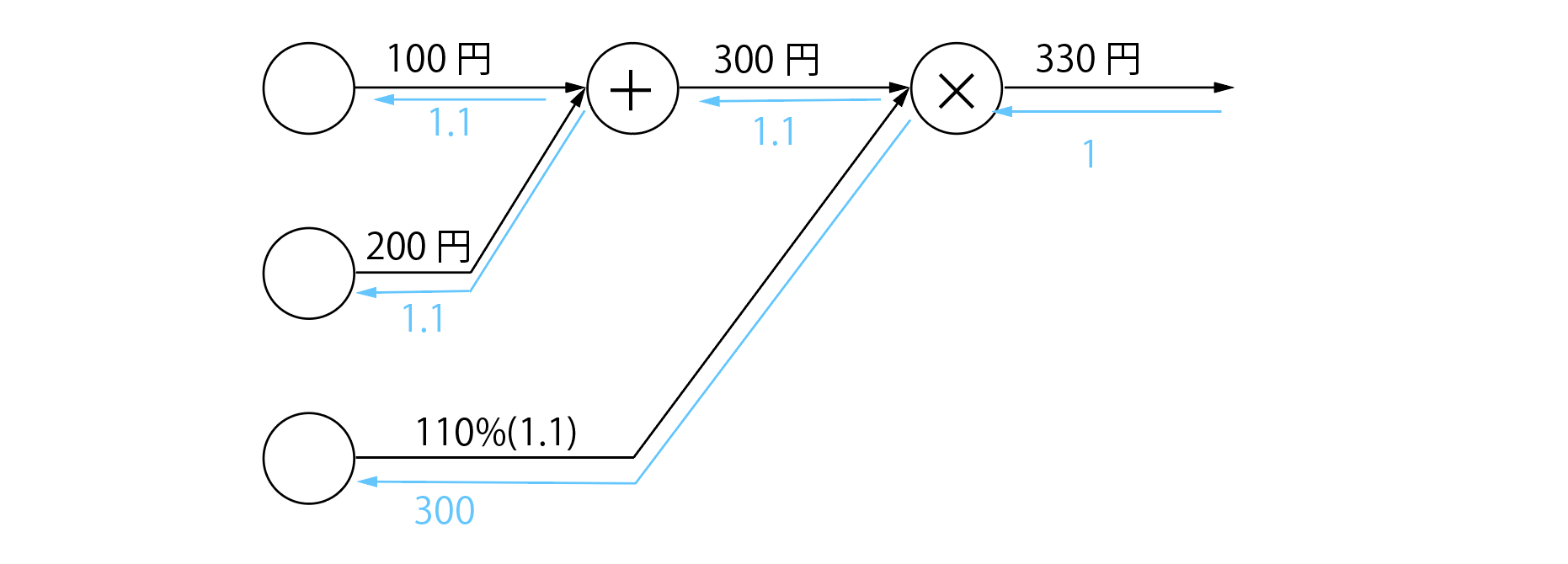
最後に、この節の問題「各値を少し変えると最終的な値にどう影響するか」を逆伝播で求めてみると、こんな感じになります。

結果は、

• リンゴの価格を1(円)変えると最終的な金額は1.1円変わる
• みかんの価格を1(円)変えると最終的な金額は1.1円変わる
• 消費税を1変えると最終的な金額は300円変わる

「各値を少し変えると最終的な値にどう影響するか」というのは「各値の勾配を求めること」です。つまり、計算グラフの逆伝播は、勾配を求めるための方法と言えます。

誤差逆伝播法

では、この計算グラフをニューラルネットワークにも適用してみましょう。
計算グラフの利点は、「複雑な計算を一つのノードに合わせることができる」ということです。
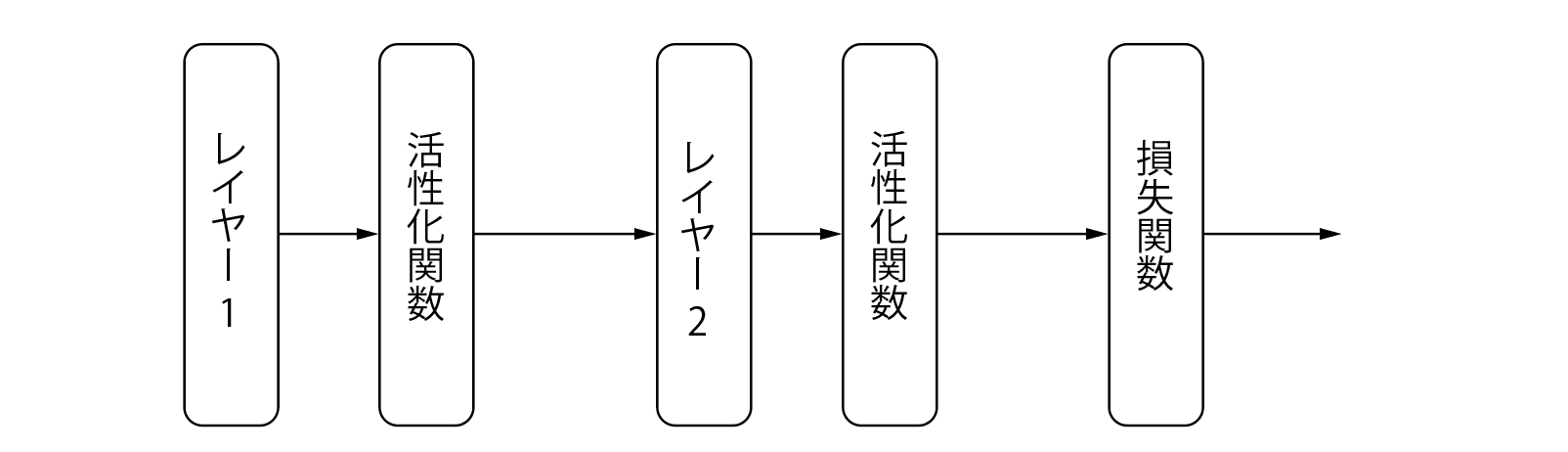
この性質を使って、まずはニューラルネットワークの簡単な計算グラフを書いてみます。こんな感じです。

ここでは、次の順番で解説していきます

• 活性化関数(relu / sigmoid / softmax)
• レイヤー(全結合層)
• 損失関数(特殊!)

活性化関数

relu

ではrelu関数の逆伝播から実装していきましょう。
ここで、relu関数の式のおさらいです。

h(x)=\left\{
\begin{array}{ll}
x & (x≥0) \\
0 & (x<0)
\end{array}
\right.

これの微分は簡単ですね。$x≥0$の時は1、$x<0$なら0です。

h(x)=\left\{
\begin{array}{ll}
1 & (x≥0) \\
0 & (x<0)
\end{array}
\right.

さて、ここで問題が一つ。relu関数の逆伝播時の$x$とは一体なんでしょうか。
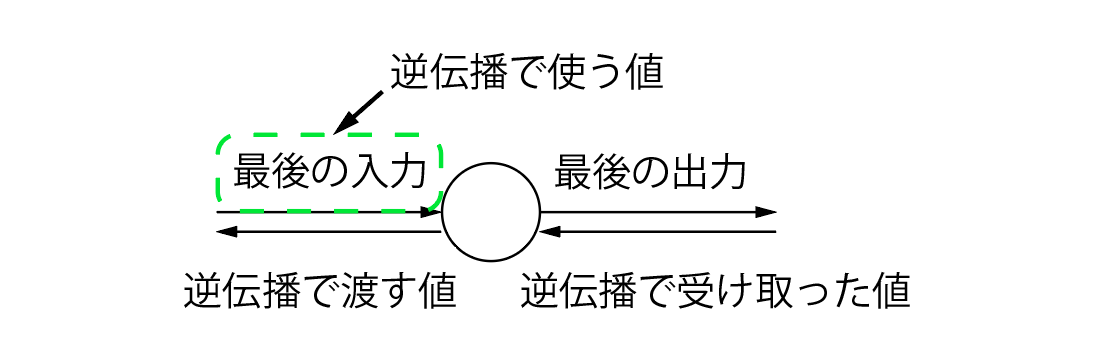
実は、relu関数に対する(対応する)入力データなのです。ある値(誤差)を受け取った時、それに対応した入力データを使って逆伝播をしていきます。図にするとこんな感じです

ただ、relu関数が受け取った全てのデータを保存しておくのはきついので、一番最後のデータだけを保持しておきます。一度推論を行って誤差を計算し、そのあとすぐに誤差逆伝播を行えばこれだけでも十分です。

では実装していきます。
この関数は、Activationクラスの新しいメンバ関数として追加しておきます。
さらに、最後の入力データを保持するメンバ変数も「last_data」として追加しておきましょう。

// forward関数を少し修正
std::vector<std::vector<long double>>forward(std::vector<std::vector<long double>> &x)
{
    last_data = x; // 変更点。ここで最後の入力を保存しておく

    /* 処理 */
}

std::vector<std::vector<long double>>relu_back(std::vector<std::vector<long double>> &x)
{
    std::vector<std::vector<long double>> res = x;

    // 対応する最後に受け取った入力が0未満なら0、そうでないのならxをそのまま
    for (int i = 0; i < x.size(); ++i)
    {
        for (int j = 0; j < x[i].size(); ++j)
        {
            if (last_data[i][j] < 0) res[i][j] = 0;
        }
    }

    return res;
}

sigmoid

つぎにsigmoid関数を実装していきましょう。これはそこそこ厄介です。
まずはsigmoid関数の式を確認

h(x)=\frac{1}{1+exp(-x)}

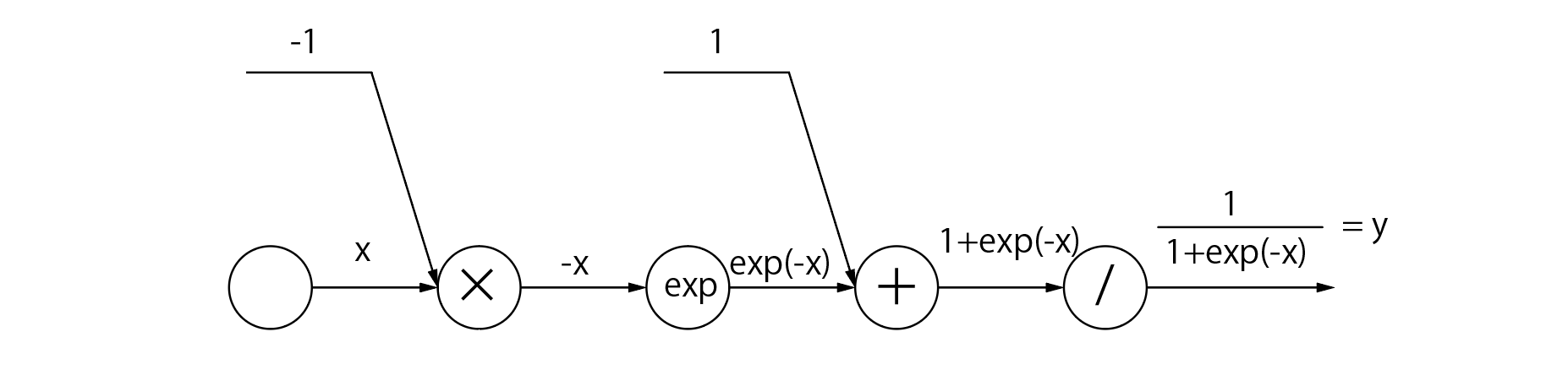
ちょっと複雑です。ということで計算グラフにしてしまいましょう。
こうなります。

難しそうですが、よくみると「exp」ノードと「/」ノードの微分さえわかれば良さそうです。

• exp(x)の微分

exp(x)の微分は、嬉しいことにexp(x)です。もちろん、このxは「×」ノードと同じく、「対応した入力」、すなわち今回の実装でいう「最後のexp(x)に対する入力」です。

• $\frac1x$ の微分

$\frac1x$の微分は、$-\frac1{x^2}$です。
また、$y=\frac1x$なので、$-y^2$と変形できます。

では、欲しかった2つの微分がわかったので、逆伝播の手順を書いてみましょう。

Eは、逆伝播時に受け取った数値・xは最後の入力・yは最後の出力です。

さて、これでsigmoid関数の微分ができました...と言いたいですが、この式、xとyと2変数あって使いづらいです。そこで、この式を変形して、こうしてしまいましょう

Ey^2exp(-x)=E\frac1{(1+exp(-x))^2}exp(-x)\\=E\frac1{1+exp(x-)}\frac{exp(-x)}{1+exp(-x)}\\=Ey(1-y)

はい、これでsigmoid関数の微分が完全にできました。

では実装していきましょう。
この関数もActivationクラスのメンバ関数として追加しちゃいます。

// sigmoid関数をちょっと修正
std::vector<std::vector<long double>>sigmoid(std::vector<std::vector<long double>> &x)
{
    /* 処理 */

    last_data = res; // 修正箇所。最後の出力を保存

    return res;
}

std::vector<std::vector<long double>>sigmoid_back(std::vector<std::vector<long double>> &x){
    std::vector<std::vector<long double>>res;

    for(int i = 0; i < x.size(); ++i){
        std::vector<long double>t;
        for(int j = 0; j < x[i].size(); ++j){
            t.push_back(x[i][j] * (1 - last_data[i][j]) * last_data[i][j]);
        }
        res.push_back(t);
    }

    return res;
}

softmax

softmax関数の逆伝播では、受け取った数値をそのまま渡すだけです。
理由は、後の損失関数の部分で説明します。

実装

std::vector<std::vector<long double>>softmax_back(std::vector<std::vector<long double>> &x){
    return x;
}

backward関数(小まとめ)

では、これまでをまとめて、backward関数として実装しましょう。これもActivationクラスの新しいメンバ関数になります。

std::vector<std::vector<long double>>backward(std::vector<std::vector<long double>> &x)
{
    if(m_name == "sigmoid") return sigmoid_back(x);
    else if(m_name == "softmax") return softmax_back(x);
    if (m_name == "relu") return relu_back(x);
    else return x;
}

レイヤー

活性化関数では、受け取った値を変換して渡す処理のみを行っていました。ですが、レイヤーではさらに「各パラメータの勾配を計算する」という作業も必要になってきます。

計算グラフ

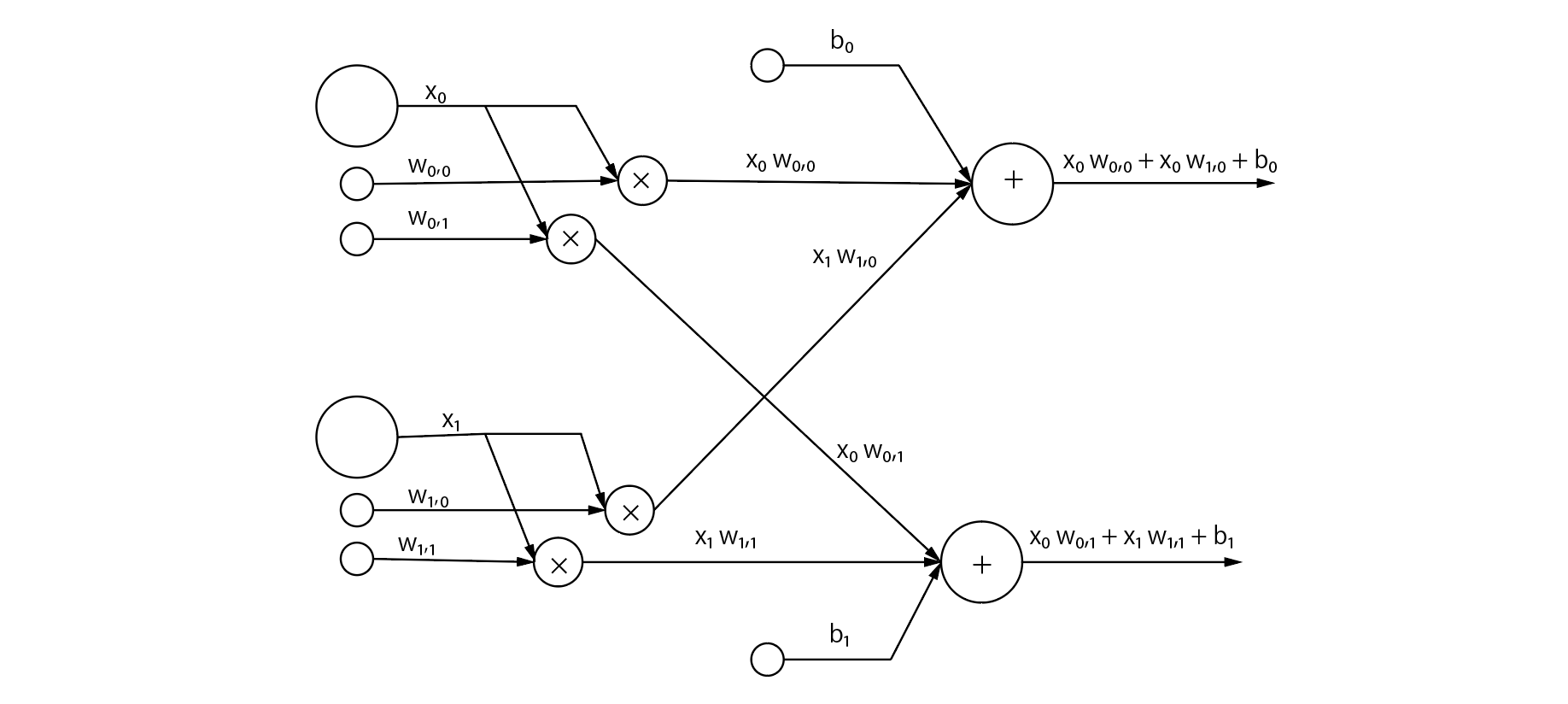
例のごとく計算グラフ。今回は2*2のレイヤーを例に説明していきます。

ごつい...
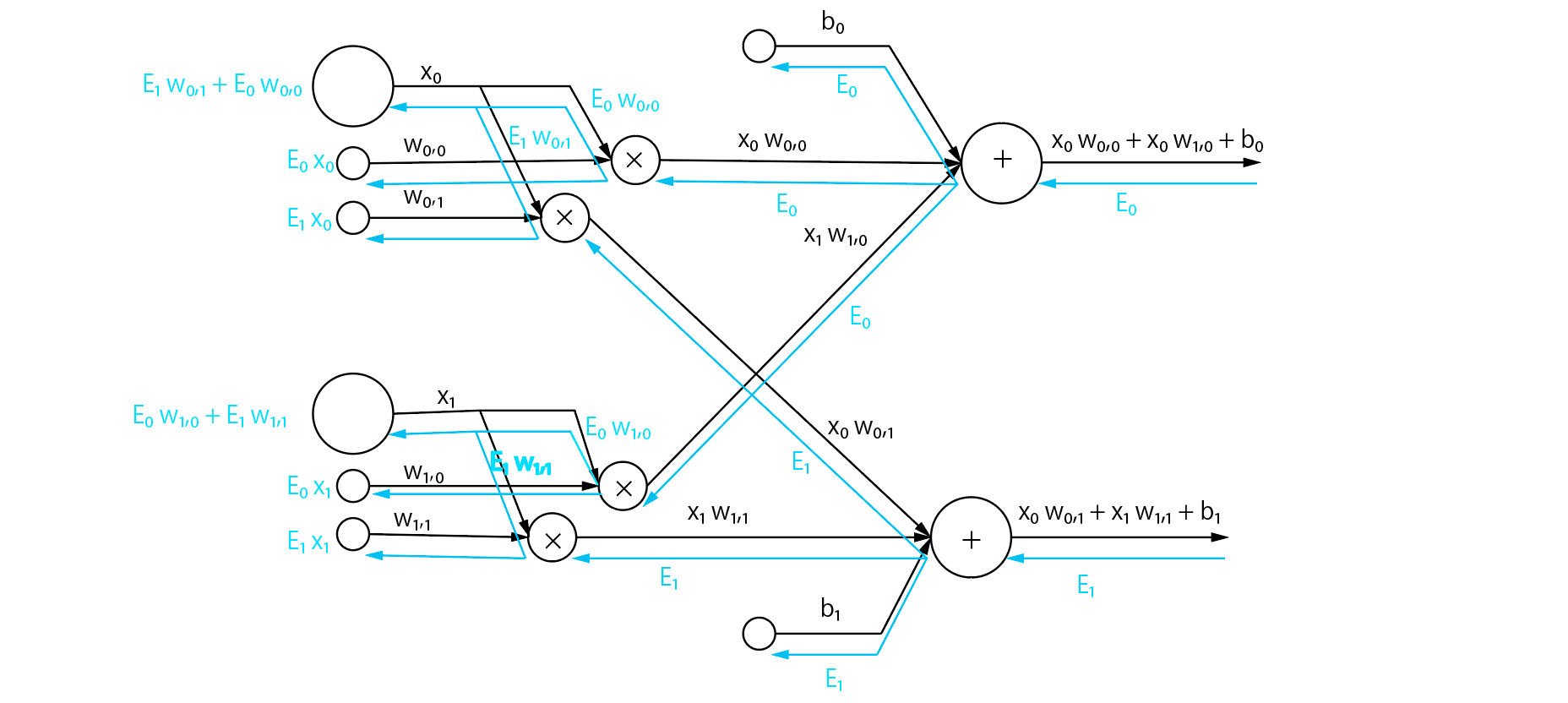
逆伝播もしちゃいましょう。こうなります。(とても見づらくてごめんなさい！)

こんな図はもう見たくないので、抽象化して式にします。

• 次の層に渡す値

X_i = \sum_j E_j\ w_{i,j}

• 重みの勾配

W_{i,j} = E_j\ x_i

• バイアスの勾配

B_i = E_i

さらにこれをバッチに対応させてみましょう。
バッチ内の全てのケースにおける式の値の和を、バッチのデータ数で割って平均にします。
ただ、上から流す値からそもそもバッチのデータ数で割ってしまいたいので、実質的にはただ足すだけです。

• 次の層に渡す値

X_{ki} = \sum_k^N \sum_{j} E_{kj}\ w_{i,j}

• 重みの勾配

W_{i,j} =\sum_k^N E_{kj}\ x_{ki}

• バイアスの勾配

B_i = \sum^N_k E_{ki}

損失関数

損失関数は結構特殊です。というのも、この記事では損失関数そのものの微分は行いません。ではどうするのかというと、最後のレイヤーのものとして想定している活性化関数と一緒に実装します。具体的には、

• 二乗和誤差→恒等関数(linear)を想定
• 交差エントロピー誤差→softmaxを想定

このように決めてしまいます。かなり危険ではありますが、そうすることで実装がこれ以上ないほどに楽になります。

では解説していきます。
結果から言うとこれら二つの組み合わせの損失関数の微分はどちらも$(y_i-t_i)$とのこと。
(ただ、二乗和誤差の方は、$\frac d{dx}x^2=2x$だから$2(y_i-t_i)$では？と思ったので、僕はこっちを採用します)
つまり、予測した値の「誤差」が一番最初に流れてくるわけです。それを「逆伝播」で次のレイヤーに伝えていくので、このような手法が「誤差逆伝播法」と呼ばれています。

二乗和誤差の方の微分は簡単ですが、交差エントロピー誤差の方は複雑で(線の交差が多い!) 、おそらく計算グラフを僕が書くと史上最高に見辛くなってしまうので、詳しく知りたい方はこのサイトなどを参照してみてください。

また、損失関数のbackward関数には、最初から$(y_i-t_i)$を渡すので、損失関数の逆伝播はその値をそっくりそのまま返すだけになります。また、softmaxが値を返すだけだったのは、ここでは損失関数と活性化関数(softmax)をつなげて考えているからです。
とりあえず実装

    std::vector<std::vector<long double>> mean_squared_error_back(std::vector<std::vector<long double>>absolute_error){
        return absolute_error; // 本だとこっち

        // 僕の思う二乗和誤差の逆伝播
        std::vector<std::vector<long double>>res;

        for(int i = 0; i < absolute_error.size(); ++i){
            std::vector<long double>t;
            for(int j = 0; j < absolute_error[i].size(); ++j){
                t.push_back(2*abs(absolute_error[i][j]));
            }
            res.push_back(t);
        }

        return res;
    }

    std::vector<std::vector<long double>> mean_cross_entropy_error_back(std::vector<std::vector<long double>>error){
        return error;
    }

実装

Denseクラス

実装の前に一つ。今回の逆伝播でも「最後に受け取った値」が必要になるので、Denseクラスに3つの新しいメンバ変数last_data grad_layer grad_biasを追加しましょう。last_dataへの代入はforward関数で行なってしまいます。
grad_layerは重みの勾配、grad_biasはバイアスの勾配を表します。

std::vector<std::vector<long double>> Layers::Dense::forward(std::vector<std::vector<long double>> &data){
    last_data=data; // 追加

    /* 処理 */

    return ans;
}

X

Xは逆伝播時に計算して次のレイヤーに渡すための値です。つまり「入力層から次の層までの誤差」です。こんな式でした。

X_{ki} = \sum_k^N \sum_{j} E_{kj}\ w_{i,j}

図を感覚で書いてしまって、$w_{i,j}$がパート1の「前の層のニューロン$j$から現在の層のニューロン$i$の重み」ではなく、「前の層のニューロン$i$から現在の層のニューロン$j$の重み」になってしまっています！ｺﾞﾒﾝﾅｻｲ!

では実装します。変数dataは前レイヤーから受け取った数値です。(数式でいう$E$)

    // dxを計算
    std::vector<std::vector<long double>> ans;
    for(int i = 0; i < data.size(); ++i){
        std::vector<long double>res;
        for(int j = 0; j < neuron[0].size(); ++j){
            long double t=0;
            for(int k = 0; k < neuron.size(); ++k){
                t += neuron[k][j] * data[i][k];
            }
            res.push_back(t);
        }
        ans.push_back(res);
    }

W

Wは逆伝播時に計算する、各パラメータの勾配を表します。式はこんな感じでした。

W_{i,j} =\sum_k^N E_{kj}\ x_{ki}

では実装していきましょう

    // dwを計算(dw : ニューロンの勾配)
    grad_layer.clear();
    for(int i = 0; i < neuron.size(); ++i){
        std::vector<long double>res;
        for(int j = 0; j < neuron[i].size(); ++j){
            long double t = 0;
            for(int k = 0; k < data.size(); ++k){
                t += data[k][i] * last_data[k][j];
            }
            res.push_back(t);
        }
        grad_layer.push_back(res);
    }

B

Bは逆伝播時に計算する、バイアスの勾配を表します。式はこんな感じでした。

B_i = \sum^N_k E_{ki}

一番簡単ですね。では実装していきます。

    // dbを計算(db : バイアスの勾配)
    grad_bias.clear();
    for(int i = 0; i < bias.size(); ++i){
        long double t = 0;
        for(int j = 0; j < data.size(); ++j){
            t += data[j][i];
        }
        grad_bias.push_back(t);
    }

backward関数(まとめ)

最後に、これら3つをまとめて新しくbackward関数としてDenseクラスのメンバ関数に追加しましょう。
活性化関数の逆伝播も忘れずに。

std::vector<std::vector<long double>>backward(std::vector<std::vector<long double>> &data){
    // 返すもの:dx
    // 返さないけど計算するもの:
    // dw, db (= 勾配)

    // まずは活性化関数を通す
    data = m_activation.backward(data);

    // dxを計算
    std::vector<std::vector<long double>> ans;
    for(int i = 0; i < data.size(); ++i){
        std::vector<long double>res;
        for(int j = 0; j < neuron[0].size(); ++j){
            long double t=0;
            for(int k = 0; k < neuron.size(); ++k){
                t += neuron[k][j] * data[i][k];
            }
            res.push_back(t);
        }
        ans.push_back(res);
    }

    // dwを計算(dw : ニューロンの勾配)
    grad_layer.clear();
    for(int i = 0; i < neuron.size(); ++i){
        std::vector<long double>res;
        for(int j = 0; j < neuron[i].size(); ++j){
            long double t = 0;
            for(int k = 0; k < data.size(); ++k){
                t += data[k][i] * last_data[k][j];
            }
            res.push_back(t);
        }
        grad_layer.push_back(res);
    }

    // dbを計算(db : バイアスの勾配)
    grad_bias.clear();
    for(int i = 0; i < bias.size(); ++i){
        long double t = 0;
        for(int j = 0; j < data.size(); ++j){
            t += data[j][i];
        }
        grad_bias.push_back(t);
    }


    return ans;
}

Modelクラス

Modelクラスの実装です。

backward関数

誤差逆伝播法を行うbackward関数を実装していきます。
と言っても、実装の大半はこれまでで終わってるので、forward関数と同じくレイヤー同士の橋渡しをするだけです。

新しいメンバ変数diff_errorが出てきました(もちろんこれも追加します)。これが$y_i-t_i$です。代入はfit関数で行います。

void backward(){
    std::vector<std::vector<long double>>data;

    // 同じだけど明示的に
    if(m_loss == "mse") data = mean_squared_error_back(diff_error);
    else data = mean_cross_entropy_error_back(diff_error);

    // forwardとは順番が逆なのに注意!
    for(int i = model.size() - 1; i>=0; --i){
        data = model[i].backward(data);
    }
}

fit関数(改造)

では最後に(ようやく最後)、パート2で実装したfit関数を改造していきましょう
改造...と言ってもコメントアウトしたり外したりするだけです。

コメントを外す箇所には// 外す!
コメントアウトする箇所はは// コメントアウト!
とコメントしてあります。

    std::vector<long double> fit(int step, long double learning_rate, std::vector<std::vector<long double>> &x, std::vector<std::vector<long double>> &y, int batch_size, std::string loss)
    {

        std::vector<long double> history;
        m_loss = loss;

        for (int current_step = 0; current_step < step; ++current_step)
        {
            std::vector<std::vector<long double>> batch_x, batch_y;
            diff_error.clear(); // 外す!
            // ミニバッチの作成
            for (int i = 0; i < batch_size; ++i)
            {
                batch_x.push_back(x[(batch_size * current_step + i) % x.size()]);
                batch_y.push_back(y[(batch_size * current_step + i) % y.size()]);
            }

            // 外す!
            // 逆伝播の準備
            auto test_y = predict(batch_x);
            for (int i = 0; i < test_y.size(); ++i)
            {
                std::vector<long double> t;
                for (int j = 0; j < test_y[i].size(); ++j)
                {
                    t.push_back((test_y[i][j] - batch_y[i][j]) / batch_size);
                }
                diff_error.push_back(t);
            }

            // 外す!
            // 逆伝播
            backward();

            long double loss_step;
            if (m_loss == "mse")
                loss_step = mean_squared_error(test_y, y);
            else
                loss_step = mean_cross_entropy_error(test_y, y);

            for (int index = 0; auto &layer : model)
            {
                // 勾配を計算
                // 数値微分(遅い)
                // コメントアウト!
                // std::vector<std::vector<long double>>layer_grad = numerical_gradient_layer(batch_x, batch_y, index);
                // std::vector<long double>bias_grad = numerical_gradient_bias(batch_x, batch_y, index);

                // 外す!
                // 誤差逆伝播法(早い)
                std::vector<std::vector<long double>> layer_grad = layer.grad_layer;
                std::vector<long double> bias_grad = layer.grad_bias;

                // 計算した勾配に従って重みを調整
                // 1.layerの調整
                for (int i = 0; i < layer_grad.size(); ++i)
                {
                    for (int j = 0; j < layer_grad[i].size(); ++j)
                    {
                        layer.neuron[i][j] -= learning_rate * layer_grad[i][j];
                    }
                }

                // 2.biasの調整
                for (int i = 0; i < bias_grad.size(); ++i)
                {
                    layer.bias[i] -= learning_rate * bias_grad[i];
                }

                ++index;
            }

            // 学習経過の記録
            // 外す!
            history.push_back(loss_step);
            // コメントアウト!
            // history.push_back(caluculate_loss(batch_x, batch_y));
        }

        return history;
    }

これで、誤差逆伝播の実装は完了です！！
お疲れ様でした！

まとめ

C++でつくるDeepLearning、いかがだったでしょうか。
普段Pythonで実装されることの多いニューラルネットワークをC++という実行速度の早い言語で実装する、とても面白い挑戦だと思います(自分で言うのもあれですが)。ニューラルネットワークには、他にも「畳み込み層」という、レイヤーや、学習効率化のための「Adam」「Momentum」などの重み更新手法、「Batch Normalization」などなど...上げ出したらキリがないほどまだまだ実装の余地があります。いつかこれらを実装して「パート4」として投稿してみたいですね
C++に限らず、どんな言語でもある程度のオブジェクト指向さえあればネットワークの実装はできると僕は信じています。
この記事で、AI(ニューラルネットワーク)の理解や、興味が深まってくれるととても嬉しいです。

おまけ(ソースコード)

ここで、誤差逆伝播法まで全てを実装したソースコードを載せておきます。
前パートと同じく、実装が追加・変更されたところには// NEW!をつけています
ちなみにmain関数では足し算をさせています。

モデルを見てもらうと、なんとユニット数が32!前回の3倍です(10だとうまく学習できませんでした。速いからヨシ!)。ですが実行してみるとパート2のユニット数10の数値微分での学習よりも遥かに速いことがわかると思います。

余談ですが、活性化関数にsigmoidではなくreluを使うと何故か学習がうまくいきませんでした。
活性化関数の向き不向きなのか、実装が間違ってるのか...
こうしてみるとまだまだ課題はありそうですね

2021/8/5追記:
どうやら最適化関数が悪かったみたい。
これまでは単純な確率的勾配降下法を使っていたけれど、AdaGradという最適化関数にしてみたらreluでもいけた。しかもsigmoid使った時よりも遥かに効率よくなってました
やっぱりrelu関数強いなぁ

一応テストはしてますが、// NEW!が消せてなかったりつけられてなかったりなどあるかもなので、あれば指摘してくれると嬉しいです。
(パート2と同じように、ここのソースコードもパート1,2と多少違うことがあるので、コピペでもしっかりと動作はしますが、それよりはNEWの部分の編集をお勧めします)

main.cpp

#include <bits/stdc++.h>

long double mean_squared_error(std::vector<std::vector<long double>> &y, std::vector<std::vector<long double>> &t)
{
    long double res = 0;
    for (int i = 0; i < y.size(); ++i)
    {
        long double sum = 0;
        for (int j = 0; j < y[0].size(); ++j)
        {
            sum += (y[i][j] - t[i][j]) * (y[i][j] - t[i][j]);
        }

        sum /= 2 * y.size();
        res += sum;
    }

    return res;
}

long double mean_cross_entropy_error(std::vector<std::vector<long double>> &y, std::vector<std::vector<long double>> &t)
{
    long double res = 0;
    for (int i = 0; i < y.size(); ++i)
    {
        long double sum = 0;
        long double delta = 1e-7;
        for (int j = 0; j < y[0].size(); ++j)
        {
            // y[i][j]が0だとバグが起きるのでdeltaを加算して計算
            sum += t[i][j] * std::log(y[i][j] + delta);
        }
        sum *= -1;
        res += sum;
    }
    return res / y.size();
}

// NEW!
std::vector<std::vector<long double>> mean_squared_error_back(std::vector<std::vector<long double>> absolute_error)
{
    return absolute_error; // 本だとこっち

    // 僕の思う二乗和誤差の逆伝播
    std::vector<std::vector<long double>> res;

    for (int i = 0; i < absolute_error.size(); ++i)
    {
        std::vector<long double> t;
        for (int j = 0; j < absolute_error[i].size(); ++j)
        {
            t.push_back(2 * abs(absolute_error[i][j]));
        }
        res.push_back(t);
    }

    return res;
}

// NEW!
std::vector<std::vector<long double>> mean_cross_entropy_error_back(std::vector<std::vector<long double>> error)
{
    return error;
}

class Activation
{
    /* sigmoid関数の定義 */
    std::vector<std::vector<long double>> sigmoid(std::vector<std::vector<long double>> &x)
    {
        std::vector<std::vector<long double>> res;

        for (auto batch : x)
        {
            // バッチごとに処理
            std::vector<long double> t;
            for (auto i : batch)
            {
                t.push_back(1.0 / (1.0 + exp(-i)));
            }
            res.push_back(t);
        }

        last_data = res; // NEW!

        return res;
    }

    /* relu関数の定義 */
    std::vector<std::vector<long double>> relu(std::vector<std::vector<long double>> &x)
    {
        std::vector<std::vector<long double>> res;

        for (auto batch : x)
        {
            // バッチごとに処理
            std::vector<long double> t;
            for (long double i : batch)
            {
                t.push_back((i >= 0) * i);
            }
            res.push_back(t);
        }
        return res;
    }

    /* softmax関数の定義 */
    std::vector<std::vector<long double>> softmax(std::vector<std::vector<long double>> &x)
    {
        std::vector<std::vector<long double>> res;

        for (auto batch : x)
        {
            // バッチごとに処理
            std::vector<long double> t;
            long double c = *max_element(batch.begin(), batch.end());
            long double sum = 0;
            for (long double i : batch)
            {
                sum += exp(i - c);
            }
            for (long double i : batch)
            {
                t.push_back(exp(i - c) / sum);
            }
            res.push_back(t);
        }
        return res;
    }

    // NEW!
    std::vector<std::vector<long double>> relu_back(std::vector<std::vector<long double>> &x)
    {
        std::vector<std::vector<long double>> res = x;

        // 対応する最後に受け取った入力が0未満なら0、そうでないのならxをそのまま
        for (int i = 0; i < x.size(); ++i)
        {
            for (int j = 0; j < x[i].size(); ++j)
            {
                if (last_data[i][j] < 0) res[i][j] = 0;
            }
        }

        return res;
    }

    // NEW!
    std::vector<std::vector<long double>> sigmoid_back(std::vector<std::vector<long double>> &x)
    {
        std::vector<std::vector<long double>> res;

        for (int i = 0; i < x.size(); ++i)
        {
            std::vector<long double> t;
            for (int j = 0; j < x[i].size(); ++j)
            {
                t.push_back(x[i][j] * (1 - last_data[i][j]) * last_data[i][j]);
            }
            res.push_back(t);
        }

        return res;
    }

    // NEW!
    std::vector<std::vector<long double>> softmax_back(std::vector<std::vector<long double>> &x)
    {
        return x;
    }

    std::string m_name;
    std::vector<std::vector<long double>> last_data; // NEW!

public:
    Activation();
    Activation(std::string name) : m_name(name) {}
    /* forward関数の定義 */
    std::vector<std::vector<long double>> forward(std::vector<std::vector<long double>> &x)
    {
        last_data = x; // NEW!
        if (m_name == "sigmoid")
            return sigmoid(x);
        else if (m_name == "relu")
            return relu(x);
        else if (m_name == "softmax")
            return softmax(x);
        else
            return x;
    }

    // NEW!
    std::vector<std::vector<long double>> backward(std::vector<std::vector<long double>> &x)
    {
        if (m_name == "sigmoid")
            return sigmoid_back(x);
        else if (m_name == "softmax")
            return softmax_back(x);
        if (m_name == "relu")
            return relu_back(x);
        else
            return x;
    }
};

class Dense
{
public: // public:の位置変更
    Activation m_activation;
    std::vector<long double> bias;
    std::vector<std::vector<long double>> neuron;
    std::vector<std::vector<long double>> last_data;  // NEW!
    std::vector<std::vector<long double>> grad_layer; // NEW!
    std::vector<long double> grad_bias;               // NEW!

    // コンストラクタ
    Dense(int input_unit, int unit, std::string activation) : bias(unit),
                                                              neuron(unit, std::vector<long double>(input_unit)),
                                                              m_activation(activation)
    {

        double sigma = 0.05;
        if (activation == "relu")
            sigma = std::sqrt(2.0 / (double)input_unit);
        else if (activation == "sigmoid" || activation == "leaner")
            sigma = std::sqrt(1.0 / (double)input_unit);
        else
            sigma = 0.05;

        // 重みとバイアスを初期化
        std::random_device seed;
        std::mt19937 engine(seed());
        std::normal_distribution<> generator(0.0, sigma);

        for (int i = 0; i < unit; ++i)
        {
            bias[i] = generator(engine);
            for (int j = 0; j < input_unit; ++j)
            {
                neuron[i][j] = generator(engine);
            }
        }
    }

    // forward関数
    std::vector<std::vector<long double>> forward(std::vector<std::vector<long double>> &data)
    {
        last_data = data; // NEW!

        std::vector<std::vector<long double>> ans;

        // データごとに処理
        for (int index = 0; auto &i : data)
        {

            std::vector<long double> res;
            for (int j = 0; j < neuron.size(); ++j)
            {
                long double t = 0;
                // 入力 * 重み
                for (int k = 0; k < neuron[j].size(); ++k)
                {
                    t += i[k] * neuron[j][k];
                }

                // バイアスの適用
                t -= bias[j];

                res.push_back(t);
            }

            ans.push_back(res);

            ++index;
        }

        ans = m_activation.forward(ans); // 活性化関数を適用

        return ans;
    }

    std::vector<std::vector<long double>> backward(std::vector<std::vector<long double>> &data)
    {
        // 返すもの:dx
        // 返さないけど計算するもの:
        // dw, db (= 勾配)

        // まずは活性化関数を通す
        data = m_activation.backward(data);


        // dxを計算
        std::vector<std::vector<long double>> ans;
        for (int i = 0; i < data.size(); ++i)
        {
            std::vector<long double> res;
            for (int j = 0; j < neuron[0].size(); ++j)
            {
                long double t = 0;
                for (int k = 0; k < neuron.size(); ++k)
                {
                    t += neuron[k][j] * data[i][k];
                }
                res.push_back(t);
            }
            ans.push_back(res);
        }

        // dwを計算(dw : ニューロンの勾配)
        grad_layer.clear();
        for (int i = 0; i < neuron.size(); ++i)
        {
            std::vector<long double> res;
            for (int j = 0; j < neuron[i].size(); ++j)
            {
                long double t = 0;
                for (int k = 0; k < data.size(); ++k)
                {
                    t += data[k][i] * last_data[k][j];
                }
                res.push_back(t);
            }
            grad_layer.push_back(res);
        }

        // dbを計算(db : バイアスの勾配)
        grad_bias.clear();
        for (int i = 0; i < bias.size(); ++i)
        {
            long double t = 0;
            for (int j = 0; j < data.size(); ++j)
            {
                t += data[j][i];
            }
            grad_bias.push_back(t);
        }
        return ans;
    }
};

class Model
{
private:
    int m_input_size, m_output_size;
    std::vector<Dense> model;
    std::vector<std::vector<long double>> diff_error; // NEW!

    std::string m_loss;

    long double caluculate_loss(std::vector<std::vector<long double>> &batch_x, std::vector<std::vector<long double>> &batch_y)
    {
        // cen:考査エントロピー誤差
        // mse:二乗和誤差
        std::vector<std::vector<long double>> t = predict(batch_x);
        if (m_loss == "cen")
            return mean_cross_entropy_error(t, batch_y);
        return mean_squared_error(t, batch_y);
    }

    // NEW!
    void backward()
    {
        std::vector<std::vector<long double>> data;

        // 同じだけど明示的に
        if (m_loss == "mse")
            data = mean_squared_error_back(diff_error);
        else
            data = mean_cross_entropy_error_back(diff_error);


        // forwardとは順番が逆なのに注意!
        for (int i = model.size() - 1; i >= 0; --i)
        {
            data = model[i].backward(data);
        }
    }

    std::vector<std::vector<long double>> numerical_gradient_layer(std::vector<std::vector<long double>> &batch_x, std::vector<std::vector<long double>> &batch_y, int index)
    {
        // index:微分対象のレイヤー

        long double h = 1e-4;
        std::vector<std::vector<long double>> grad(model[index].neuron.size(), std::vector<long double>(model[index].neuron[0].size()));
        for (int i = 0; i < grad.size(); ++i)
        {
            for (int j = 0; j < grad[i].size(); ++j)
            {
                long double tmp = model[index].neuron[i][j];

                model[index].neuron[i][j] = tmp + h;                  // 1
                long double fxh1 = caluculate_loss(batch_x, batch_y); // 2

                model[index].neuron[i][j] = tmp - h;                  // 3
                long double fxh2 = caluculate_loss(batch_x, batch_y); // 4

                grad[i][j] = (fxh1 - fxh2) / (2 * h); // 5
                model[index].neuron[i][j] = tmp;
            }
        }

        return grad;
    }

    std::vector<long double> numerical_gradient_bias(std::vector<std::vector<long double>> &batch_x, std::vector<std::vector<long double>> &batch_y, int index)
    {
        long double h = 1e-4;
        std::vector<long double> grad(model[index].bias.size());
        for (int i = 0; i < grad.size(); ++i)
        {
            long double tmp = model[index].bias[i];

            model[index].bias[i] = tmp + h;                       // 1
            long double fxh1 = caluculate_loss(batch_x, batch_y); // 2

            model[index].bias[i] = tmp - h;                       // 3
            long double fxh2 = caluculate_loss(batch_x, batch_y); // 4

            grad[i] = (fxh1 - fxh2) / (2 * h); // 5
            model[index].bias[i] = tmp;
        }

        return grad;
    }

public:
    Model(int input_size) : m_input_size(input_size),
                            m_output_size(input_size)
    {
    }

    void AddDenseLayer(int unit, std::string activation)
    {
        Dense dense(m_output_size, unit, activation);
        model.push_back(dense);
        m_output_size = unit;
    }
    std::vector<std::vector<long double>> predict(const std::vector<std::vector<long double>> &data)
    {
        std::vector<std::vector<long double>> res = data;
        for (auto &layer : model)
        {
            res = layer.forward(res);
        }

        return res;
    }

    std::vector<long double> fit(int step, long double learning_rate, std::vector<std::vector<long double>> &x, std::vector<std::vector<long double>> &y, int batch_size, std::string loss)
    {

        std::vector<long double> history;
        m_loss = loss;

        for (int current_step = 0; current_step < step; ++current_step)
        {
            std::vector<std::vector<long double>> batch_x, batch_y;
            diff_error.clear(); // NEW!
            for (int i = 0; i < batch_size; ++i)
            {
                batch_x.push_back(x[(batch_size * current_step + i) % x.size()]);
                batch_y.push_back(y[(batch_size * current_step + i) % y.size()]);
            }

            // 逆伝播の準備 // NEW!
            auto test_y = predict(batch_x);
            for (int i = 0; i < test_y.size(); ++i)
            {
                std::vector<long double> t;
                for (int j = 0; j < test_y[i].size(); ++j)
                {
                    t.push_back((test_y[i][j] - batch_y[i][j]) / batch_size);
                }
                diff_error.push_back(t);
            }

            // 逆伝播 // NEW!
            backward();

            long double loss_step;
            if (m_loss == "mse")
                loss_step = mean_squared_error(test_y, y);
            else
                loss_step = mean_cross_entropy_error(test_y, y);

            for (int index = 0; auto &layer : model)
            {
                // 勾配を計算
                // 数値微分(遅い) // NEW!
                // std::vector<std::vector<long double>> layer_grad = numerical_gradient_layer(batch_x, batch_y, index);
                // std::vector<long double> bias_grad = numerical_gradient_bias(batch_x, batch_y, index);

                // 誤差逆伝播法(早い) // NEW!
                std::vector<std::vector<long double>> layer_grad = layer.grad_layer;
                std::vector<long double> bias_grad = layer.grad_bias;

                // 計算した勾配に従って重みを調整
                // 1.layerの調整
                for (int i = 0; i < layer_grad.size(); ++i)
                {
                    for (int j = 0; j < layer_grad[i].size(); ++j)
                    {
                        layer.neuron[i][j] -= learning_rate * layer_grad[i][j];
                    }
                }


                // 2.biasの調整
                for (int i = 0; i < bias_grad.size(); ++i)
                {
                    layer.bias[i] -= learning_rate * bias_grad[i];
                }

                ++index;
            }

            // 学習経過の記録
            history.push_back(loss_step); // NEW!
            // history.push_back(caluculate_loss(batch_x, batch_y)); // NEW!
        }

        return history;
    }
};

int main()
{
    Model model(2);

    model.AddDenseLayer(32, "sigmoid");
    model.AddDenseLayer(1, "linear");

    std::vector<std::vector<long double>> x = {
        {3, 7},
        {1, 5},
        {4, 3},
        {7, 9}};

    std::vector<std::vector<long double>> y = {
        {10},
        {6},
        {7},
        {16}};

    auto t = model.predict(x);

    for (auto i : t)
    {
        for (auto j : i)
            std::cout << j << " ";
        std::cout << std::endl;
    }


    auto history = model.fit(1000, 0.1, x, y, 4, "mse");

    t = model.predict(x);

    std::cout << std::endl;

    for (auto i : t)
    {
        for (auto j : i)
            std::cout << j << " ";
        std::cout << std::endl;
    }
}