Google Code Jam 2018 Qualification Round

Rubyで挑戦。1,2,4問目を完全に解いて70点でした。

Googleの発表によれば、各人数は次の通り。
62,000 登録者数
24,000 1回以上提出した人数
21,000 1点以上の人数
14,000 25点以上取った人(=予選を通過してRound 1に進んだ人)

各問題で自分が解答したときの方針と、提出コードをまとめました。

Saving The Universe Again

「一番右のSの塊のうち、一番左のS」を見つけて、左のCと入れ替える。(解説見たら一番右の「CS」という文字列と説明している……そっちのほうが分かりやすい)
1回入れ替えるごとに得点を計算して、ダメージがD未満ならOK。

最初、例を入力しても結果が合わなかった。「ダメージをD以下にする(原文：no more than D total damage)」の箇所を「ダメージをD未満にする」と勘違いして実装していたためである。そこを直したら入力例に対して正しくなったので、そのまま提出。

N = gets().to_i

def calc_damage(str)
	sum = 0
	dam = 1
	str.each_char { |c|
		if c == "C"
			dam *= 2
		elsif c == "S"
			sum += dam
		end
	}
	return sum
end

N.times do |t|
	input = gets().chomp!.split
	th = input[0].to_i
	str = input[1]
	
	ans = 0
	while true do
		# ダメージ値を計算
		damage = calc_damage(str)
		if damage <= th then
			#値が閾値より小さかったら終了
			puts "Case ##{t+1}: #{ans}"
			break #★1ケース終わり
		end

		# 最も後方のS塊の最初のSを探す、手前のCと交換
		flag = false
		pos = -1
		str.length().downto(0) { |i|
			if str[i] == "S" then
				flag = true
			end
			if flag && i > 0 && str[i-1] =="C" then
				pos = i
				break
			end
		}

		if pos == -1 then
			# そいつが先頭だったらimpossible(全てのSが最初に集結しているので、これ以上減らない)
			# あと見つからないケースもあるが(全部C)、これは明らかに最初でans = 0と判定される
			puts "Case ##{t+1}: IMPOSSIBLE"
			break #★1ケース終わり
		end

		str[pos-1] = "S"
		str[pos] = "C"
		ans += 1
	end
end

Trouble Sort

愚直に操作を実施していくと計算量が$O(N^2)$になる。入力される数列の要素数が$10^5$なので間に合わない。計算量を減らす工夫が必要だ。
2つ隣の要素と入れ替えているので、偶数番目・奇数番目に分けてバブルソートをしていることが分かる。
従って、入力された数列を偶数番目・奇数番目に分けた後にそれぞれをソートし、全体が非減少となっているか確認すれば良い。分けた数列を元通りに繋ぎ合わせなくても、非減少の確認は可能である。しかし「繋ぎ合わせたほうが確実かな……」と思ったので繋ぎ合わせている。(2つの配列を互い違いに組み合わせるなんていう便利メソッドはないので、zipで組み合わせた後flattenで配列を一重にした)
あと、配列の偶数番目だけ抜き出す方法は、エイヤッとググって下記を参考にした。
[Java][Ruby] 配列の偶数番目の要素を抜き出す: 遠回りするかな

N = gets().to_i

N.times do |t|
	m = gets().to_i
	arr = gets().split.map { |k|
		k.to_i
	}
	arr_first = arr.select.with_index{|e, i|
	  i % 2 == 0
	}
	arr_second = arr.select.with_index{|e, i|
	  i % 2 == 1
	}

	arr_first.sort!
	arr_second.sort!

	# make the array again. (though it is not necessary)
	arr = arr_first.zip(arr_second).flatten

	if(arr[-1] == nil) then
		arr.delete_at(-1)
	end

	is_sorted = false
	0.upto(arr.length-2) do |i|
		if arr[i] > arr[i+1] then
			puts "Case ##{t+1}: #{i}"
			is_sorted = true
			break
		end
	end
	if (!is_sorted) then
		puts "Case ##{t+1}: OK"
	end
end

Cubic UFO

Go, Gopher!の問題文を読んで「ランダム要素が入ってきて決定的に解けないから、場合分けが面倒そう……嫌だな……」と思いながらCubic UFOを見たら、思いの外簡単だった。「え、visibleだけ解くんならこっちのほうが簡単じゃない!?」と思ってvisibleだけの解を書き、その後hiddenも解ける解を書いて提出。
数学的考察を要求する問題、大好き。基本的には解説と同じ。

・visible
下の図を参照!
図は横から見たもの。

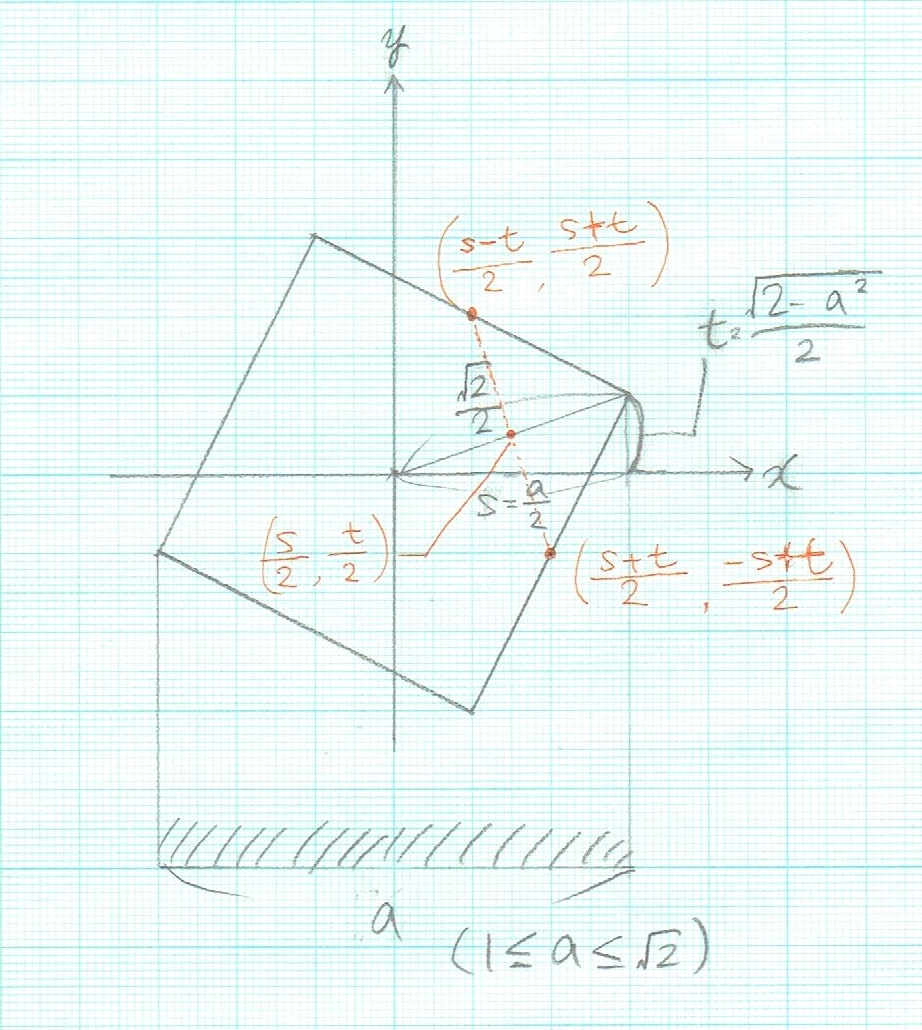
影の面積は1×a = aである。したがって指定される値はaに等しい。
回転角を0～45度で二分探索しようかと一瞬考えた。しかし、落ち着いて考えると入力値が分かればsがわかり、sが分かればtも分かるので、解答は一意に定まる。
今までの問題に比べてコードはずっと短い。競技プログラミングというより数学の問題みたいだな。

N = gets().to_i

N.times do |j|
	puts "Case ##{j+1}:"
	a = gets().to_f
	s = a/2
	if 2-a**2 < 0 then
		exit
	else
		t = Math.sqrt(2-a**2)/2
	end

	puts "#{(s+t)/2} #{(-s+t)/2} 0"
	puts "#{(s-t)/2} #{(s+t)/2} 0"
	puts "0 0 0.5"
end

・hidden
下の図を参照!!
1から$\sqrt 3$に単調増加するような回転の仕方を上手く構成できるかがポイント。図は真上から見たところ。

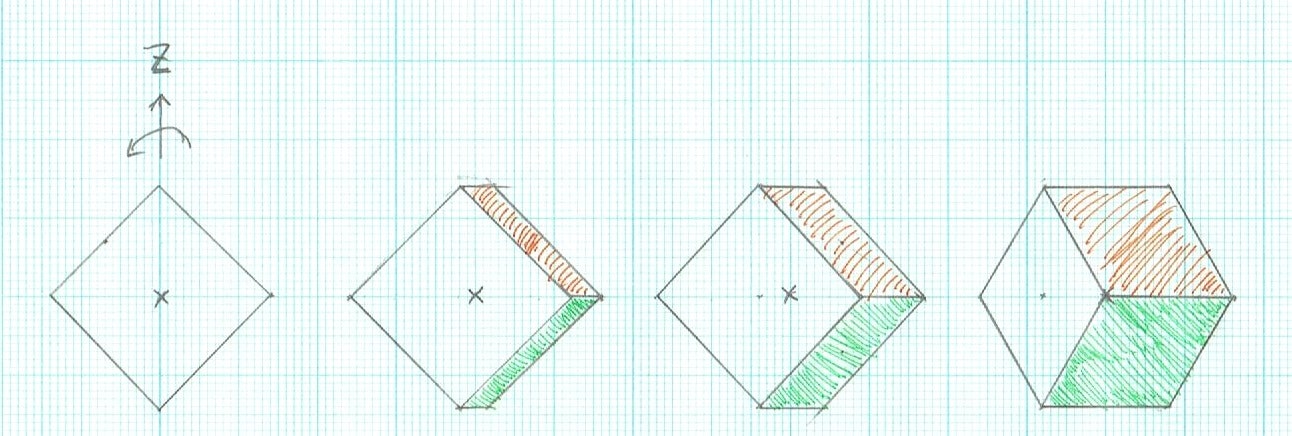
z軸周りに回転させると2つの面が少しずつ見えて面積が増加する。回し続けると3つの面が対称に見えるところがあり、これが影の面積が最大($\sqrt 3$)になる場合である。

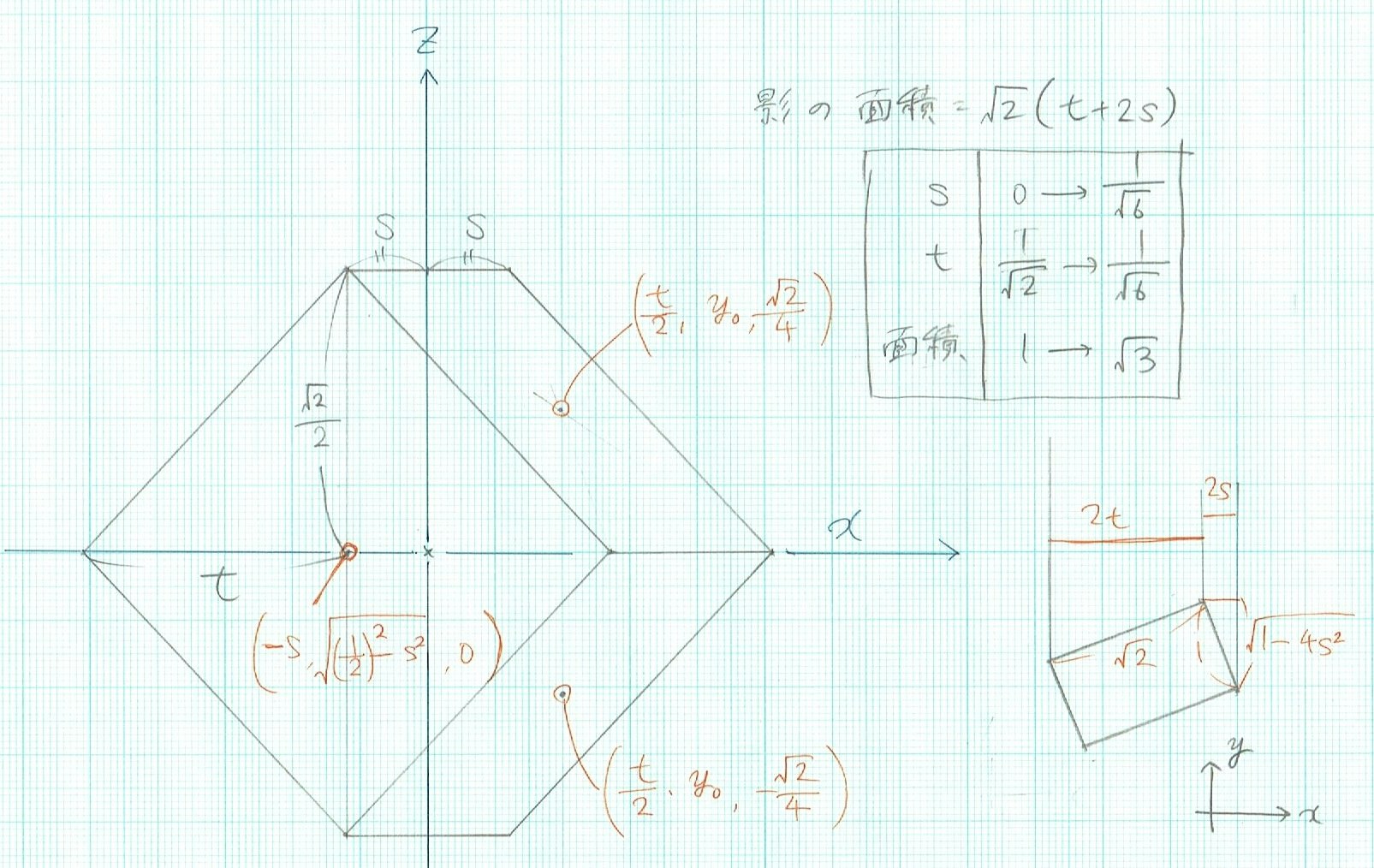
大きな図は上から見たところ。右下の長方形はxy平面で切ったときの切り口を横から見たところ。
sとtの関係は上図の右下部分を参照。xy平面で切ったときの切り口は「1×$\sqrt 2$」の長方形になっている。三平方の定理と相似比を使うと、$t = \sqrt{\frac{1}{2}-2s^2}$という関係式が求まる。

これはsを直接求めるのが困難なので、面積がsに関する単調増加関数である(証明してないけどきっとそうだろう)ことを利用して二分探索で解く。
面積が指定されたら、sについて二分探索を実行して、面積が指定された値となるようなsを求める。
実際に出力すべきは各面の中心の座標であり、それは図の中に書いたとおり。なお、$y_0$の値は三平方の定理から求まる。

N = gets().to_i

def calc_area(s)
	t = Math.sqrt(0.5 - 2 * s**2)
	return Math.sqrt(2) * (t+2*s)
end

MAX_S = 1 / Math.sqrt(6)

N.times do |j|
	target = gets().to_f
	puts "Case ##{j+1}:"

	upper = MAX_S
	lower = 0
	s = (upper + lower) / 2

	while true do 
		area = calc_area(s)
		if (target - area).abs <= 0.0000001 # 1/10 of the problem
			break
		end

		if (area > target) then
			# decrease s
			upper = s
			s = (upper + lower) / 2
		else 
			# increase s
			lower = s
			s = (upper + lower) / 2
		end
	end

	t = Math.sqrt(0.5 - 2 * s**2)
	u = Math.sqrt(0.125 - (t**2)/4)

	puts "#{-s} #{Math.sqrt((1.to_f)/4 -s**2)} 0"
	puts "#{t/2} #{u} #{ Math.sqrt(2)/4}"
	puts "#{t/2} #{u} #{-Math.sqrt(2)/4}"
end

• 一回の回転で影の面積が1から$\sqrt 3$に増えるように工夫した。これは不必要な場合分けを回避するため
• sin, cosの三角関数を排除して、角度ではなくsの値で二分探索する。回転行列とかを持ち出さずに単純な式で書ければ、数式がややこしくならずに済むので、コードも書きやすいかな、と。
• 指定された面積と、出力した座標で定まる面積の差は10^-7以下となるようにした。問題では「10^-6以下ならOK」としているが、そのとおり実装すると数値誤差か何かの影響で誤差がギリギリ10^-6より大きくなるのではないかと懸念したためである。