五目並べチェッカー
はじめに
Twitterでchokudaiさんのツイートを見ました。
個人的に、「これが解ければ業務任せてもロジック部分は安心だな!」って思える問題は五目並べチェッカーなのよね。https://t.co/wIKuygqlzs
— chokudai(高橋 直大)🍆🍡🌸 (@chokudai) June 17, 2019
この問題ができたら業務を任せても安心なレベルらしいので、さっそく挑戦してみました。
問題
方針を考える
コードを書き始める前に、まず何を実現する必要があるのか考えます。問題文に書いてあるとおり、以下の2つの場合がないかどうかを検索したいです。
- どちらかのプレーヤーの勝利条件を満たしているのに、もう片方のプレーヤーがさらに碁石を置いている。
- お互いが置いた個数がありえない状態になっている。
まず個数についてカウントし、以下の3つのパターンのどれかであることを確認しましょう。
- 黒が白より1個多い(最後に行動したのは黒)
- 黒と白が同じ個数(最後に行動したのは白)
- 盤面に何も石が置いていない
(ちなみに私が最初に提出したコードで、黒石と白石の個数の差が1個以下であればOKとしてしまったのですがACになりました。白石が黒石より1個多い場合はOKではないので嘘解法ですが、それはテストケースに含まれていなかったみたいです。)
個数を確認できたら、以下の手順で勝利条件の確認をします。
- 現在の盤面で両者ともに勝利条件を満たしていなければOK
- 最後に行動したプレイヤーの石をどれか取り除いてみて、その状態で両者ともに勝利条件を満たしていなければOK
五目並べの勝利条件とは、5つ以上の碁石が縦・横・ななめに並んでいることです。これを確認するためには碁盤の縦・横・ななめを1次元の配列で取り出して連続する碁石の数を数えれば良さそうです。
実装
方針が決まったので、さっそくコードを実装していきます。それなりに長くて複雑になりそうなので、クラスで定義してメソッドを分割して書くことにしました。
class Checker:
def __init__(self):
self.grid = []
self.black = 0
self.white = 0
self.normal = False
self.size = 19
使いそうなインスタンス変数を定義しておきます。self.gridは碁盤を2次元配列で入れるために使います。self.blackとself.whiteは黒石と白石をカウントした個数を入れます。self.normalは碁盤が正常な状態かどうか判定した結果を入れます。今回は碁盤の大きさが19x19で決まっていますが、汎用性を持たせたいのでself.sizeに大きさを入れておきます。
def make(self):
for _ in range(self.size):
row = list(input())
self.grid.append(row)
まずは標準入力を受け取って碁盤を作成します。各行の碁盤の状態が文字列で入力されるので、list(input())で配列に変換しています。ここでself.gridは以下のような2次元配列になっています。
[['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', 'x', '.', '.', '.', '.', '.', '.', 'o', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', 'o', '.', '.', '.', '.', 'o', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', 'x', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', 'o', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', 'x', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.', '.']]
def count(self):
for row in self.grid:
self.black += row.count("o")
self.white += row.count("x")
碁盤においてある碁石の数をカウントします。各行ごとに配列で取り出して"o"と"x"がいくつあるのかcountで数えて足し合わせればよいです。
def judge(self):
self.count()
if self.black == self.white + 1:
check = "o"
elif self.black == self.white:
check = "x"
else:
return
self.isnormal()
if self.normal:
return
for r in range(self.size):
for c in range(self.size):
if self.grid[r][c] == check:
self.grid[r][c] = "."
self.isnormal()
if self.normal:
return
self.grid[r][c] = check
最初に方針で確認したとおりまず個数についてカウントし、以下の3つのパターンのどれかであることを確認しましょう。
- 黒が白より1個多い(最後に行動したのは黒)
- 黒と白が同じ個数(最後に行動したのは白)
- 盤面に何も石が置いていない
今回のコードでは盤面に何も石が置かれていない場合は、場合分けしなくても正しく判定できるます。黒石の個数が白石より1個多いか、同じであることを確認して、それぞれ最後に行動したプレイヤーがどちらなのかを決めます。最後に行動したプレイヤーが黒石oまたは白石xであることをcheckという変数に入れました。
石の個数が異常な場合はそのままreturnします。self.normalの初期値はFalseにしてあるので、盤面が異常であることを返しています。
個数が正しいことが確認できたら、以下の手順で勝利条件の確認をします。
- 現在の盤面で両者ともに勝利条件を満たしていなければOK
- 最後に行動したプレイヤーの石をどれか取り除いてみて、その状態で両者ともに勝利条件を満たしていなければOK
盤面が勝利条件を満たしていないことをisnormalで判定することにします。(これは後で書きましょう)
まず現在の盤面で判定し、ここでself.normalがTrueになっていれば盤面が正常であることを返します。
そうでなければ最後に行動したプレイヤーの石をどれか1つ取り除いてみます。各行(r)、各列(c)ごとにすべてのマス目を見ていきます。マス目にcheckで決めておいた石が置かれていたらいったん取り除いて、isnormalで判定します。これでself.normalがTrueになればOKでありreturnします。そうでなければ石をもとに戻して、次のマス目を見ます。
最後まで確認してself.normalがFalseのままであれば、そのままこのメソッドを終了します。
def isnormal(self):
self.normal = True
for row in self.grid:
self.combo(row)
for col in zip(*self.grid):
self.combo(col)
field = []
for row in self.grid:
field_row = ["."] * self.size + row + ["."] * self.size
field.append(field_row)
for c in range(self.size * 2):
check_arr = []
for r in range(self.size):
check_arr.append(field[r][r+c])
self.combo(check_arr)
for c in range(self.size * 2):
check_arr = []
for r in range(self.size):
check_arr.append(field[r][self.size+c-r])
self.combo(check_arr)
次にisnormalを書きましょう。このメソッドの内部ではself.normalをまずTrueにしておき、縦・横・ななめのどれかで5つ以上連続する石があった場合にself.normalをFalseにします。縦・横・ななめのすべての検索でFalseにならなければ、self.normalがTrueのままメソッドが終了します。
配列を入れると連続する最大の個数を判定するcomboというメソッドを使うことにします。(これは後で書きましょう)
行ごとに配列を取り出してcomboに渡します。列ごとに取り出す場合はzip(*self.grid)で同様に配列を取り出します。
zipは以下のような挙動をします。配列がリストではなくタプルに出てくることに注意しておきます。後でcomboで判定するときに問題が出てくるようであれば、ここでリストに変換してからcomboに渡すことにします。
grid = [[1, 2, 3], [4, 5, 6]]
for col in zip(*grid):
print(col)
(1, 4)
(2, 5)
(3, 6)
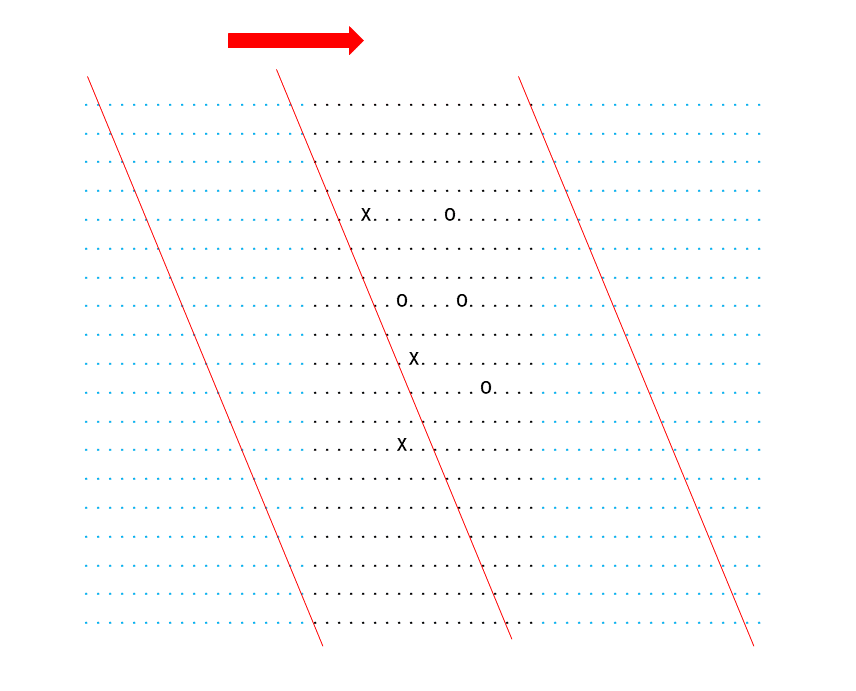
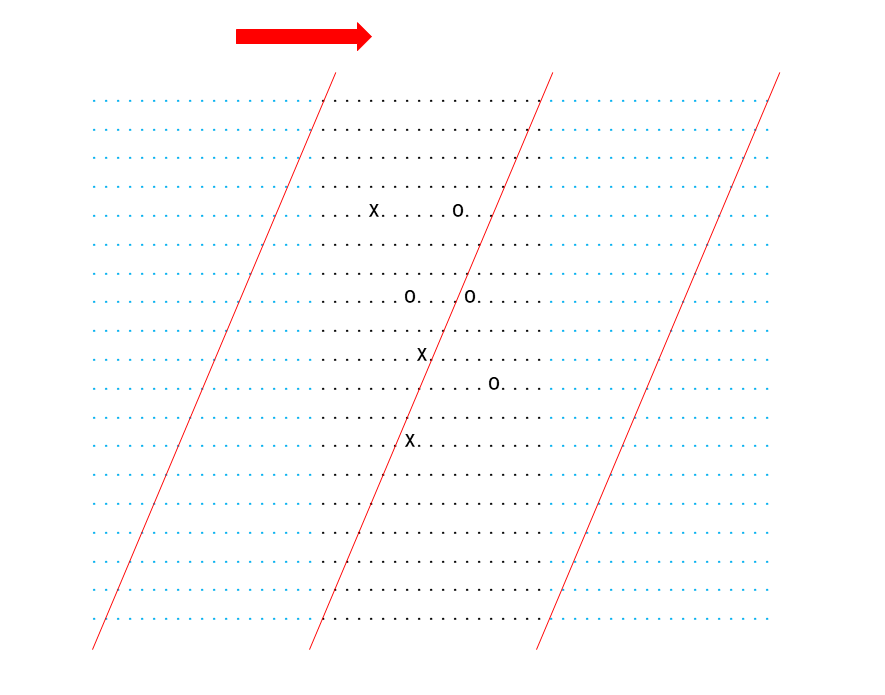
次が今回の問題で一番面倒な、ななめの判定です。self.gridをななめに見て配列を取り出していきます。このようなときグリッドの周囲に空白のマスを付け加えておくと、書きやすいです。
黒色の点が碁盤で、空白のマス目(図の水色の点)を左右に付け足しています。このようにすることでななめを判定するときに碁盤の左右にはみ出してしまう問題を簡単に解決できます。
つけたしてできたグリッドをfieldとします。これに対してfield[r][r+c]を見ていくと右下方向に向かうななめの配列を取り出せます。
同様にfield[r][self.size+c-r]を見ていくと左下方向のななめの配列が取り出せます。それぞれcomboに渡して判定します。
def combo(self, arr):
curr = "."
combo = 0
max_combo = 0
for item in arr:
if item in ["o", "x"]:
if item == curr:
combo += 1
else:
curr = item
combo = 1
max_combo = max(max_combo, combo)
else:
curr = "."
if max_combo >= 5:
self.normal = False
最後に連続する碁石の数を判定するcomboを作ります。同じ石が連続していたらcomboを増やしていき、最大値をmax_comboとします。これが5以上であればself.normalをFalseにしています。
def print(self):
print("YES" if self.normal else "NO")
問題文の形式に合わせた出力を行います。
それではすべてのメソッドをまとめて、実行してみましょう。
class Checker:
def __init__(self):
self.grid = []
self.black = 0
self.white = 0
self.normal = False
self.size = 19
def print(self):
print("YES" if self.normal else "NO")
def count(self):
for row in self.grid:
self.black += row.count("o")
self.white += row.count("x")
def make(self):
for _ in range(self.size):
row = list(input())
self.grid.append(row)
def judge(self):
self.count()
if self.black == self.white + 1:
check = "o"
elif self.black == self.white:
check = "x"
else:
return
self.isnormal()
if self.normal:
return
for r in range(self.size):
for c in range(self.size):
if self.grid[r][c] == check:
self.grid[r][c] = "."
self.isnormal()
if self.normal:
return
self.grid[r][c] = check
def combo(self, arr):
curr = "."
combo = 0
max_combo = 0
for item in arr:
if item in ["o", "x"]:
if item == curr:
combo += 1
else:
curr = item
combo = 1
max_combo = max(max_combo, combo)
else:
curr = "."
if max_combo >= 5:
self.normal = False
def isnormal(self):
self.normal = True
for row in self.grid:
self.combo(row)
for col in zip(*self.grid):
self.combo(col)
field = []
for row in self.grid:
field_row = ["."] * self.size + row + ["."] * self.size
field.append(field_row)
for c in range(self.size * 2):
check_arr = []
for r in range(self.size):
check_arr.append(field[r][r+c])
self.combo(check_arr)
for c in range(self.size * 2):
check_arr = []
for r in range(self.size):
check_arr.append(field[r][self.size+c-r])
self.combo(check_arr)
game = Checker()
game.make()
game.judge()
game.print()
問題のテストケースを入れると正しくYESとNOで判定されます。無事にACになりました。