コインを2000回投げて表が1100回以上出る確率

#コインを2000回投げて表が1100回以上出る確率

Twitterでクイズとして出題してみた問題の解答です。

★分散についての確率クイズです★

表と裏が出る確率が同じコインがあります。
このコインを2000回投げたときに、表が1100回以上出る確率はどれくらいでしょうか？

以下の選択肢から最も近い値を選んでください。

— Lillian (@Lily0727K) 2019年5月10日

###コイン投げ

まずは簡単な場合でコインを4回投げた場合を計算してみます。

表が出る回数	確率
0回	1/16
1回	4/16
2回	6/16
3回	4/16
4回	1/16

例えば4回中2回が表になる確率は以下のように求められます。

_4\rm C_2\times\left( \frac{1}{2} \right)^4 = \frac{6}{16}

より一般に、試行回数n回のうち表がk回出る確率を計算する式は以下のようになります。

_n\rm C_k \left( \frac{1}{2} \right)^n

###二項分布
コインを投げたときに表が出るか裏が出るかのように起こる結果が2つしかない試行のことをベルヌーイ試行といいます。
1回の試行において、片方の事象が起きる確率をpとします。
このベルヌーイ試行を$n$回行って、その事象が起きる回数を確率変数$X$とすると、

P(X = x) = {}_n\mathrm{C}_xp^x(1 - p)^{n - x}

となります。これに対する確率分布を二項分布(binomial distribution)と呼びます。

二項分布の期待値と分散は以下の式で表されます。

E(X) = np \\
V(X) = np(1 - p)

###正規分布に近似して計算する

二項分布の確率を計算したいですが、n = 2000という値に対して手計算することは不可能です。

実はnが十分大きいとき、二項分布は正規分布によって良好に近似されることが知られています。
これはラプラスの定理と呼ばれ、前述の平均と分散を持った正規分布として近似することができます。

今回の例では以下の値になります。

E(X) = 1000 \\
V(X) = 500

標準偏差は分散の平方根を計算して求めます。

\sigma = \sqrt{V(X)}  = \sqrt{500} \fallingdotseq 22.36

これで何が嬉しいかというと、すべての正規分布は以下の性質を示すのです。

得られた結果と平均値との差が

• ±σの範囲におさまる確率は約70%(68.27%)
• ±2σの範囲におさまる確率は約95%(95.45%)
• ±3σの範囲におさまる確率は約99%(99.73%)

つまり今回のコイン投げでは

• ±σ(978～1022回)の範囲におさまる確率は約70%
• ±2σ(956～1044回)の範囲におさまる確率は約95%
• ±3σ(933～1067回)の範囲におさまる確率は約99.73%

今回はそれ以上に離れています。正規分布表を見てみましょう。

• ±4σ(911～1089回)の範囲におさまる確率は約99.9936%
• ±4.5σ(900～1100回)の範囲におさまる確率は約99.99932%

±4.5σの範囲におさまらないのは、+4.5σ以上になるか、-4.5σ以下になるかで、それぞれの確率は同じです。
求めたいのは+4.5σ以上になる場合で、100%から99.99932%を引いて、2で割れば良いです。
計算すると、おおよそ0.00034%になりました。

問題点として1000 + 4.5σは1100.62ですが、正確に1100ではありません。
また、二項分布を正規分布とみなして計算していますが、あくまで近似なので誤差があります。

厳密に正確な値を求めることは可能でしょうか。

###二項分布を厳密に計算する

プログラムを使って計算すれば、確率を厳密に計算することができます。
ここではExcel, Python, Rの3種類での計算の仕方を示します。
それぞれ二項分布の計算用の関数が用意されていて、簡便かつ高速に結果を知ることができます。

###Excelの場合
好きなマスに以下の式をそのままコピーして貼ればよいです。
= 1 - BINOM.DIST(1099, 2000, 0.5, TRUE)

BINOM.DIST関数は二項分布の確率を計算してくれる関数です。
書式はBINOM.DIST(成功数,試行回数,成功率,関数形式)です。
関数形式にTRUEを指定した場合、0から指定した成功数までの範囲で成功が得られる確率が計算されます。

BINOM.DIST(1099, 2000, 0.5, TRUE)で表が出る回数が0～1099回の確率を計算されます。
これを1から引くと、1100回以上の確率になります。

もしくは表が1100回以上でるのは、裏が出る回数が900回以下の場合と同じなので
= BINOM.DIST(900,2000,0.5,TRUE)
として計算しても良いです。

今回は見やすいようにセルの形式を%表記に指定しています。

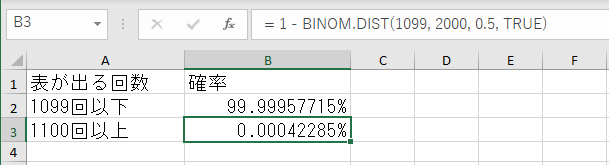
近似せずに求めた正確な値は0.00042285%でした。

###Pythonの場合
以下のライブラリを読み込むと二項分布を計算することができます。
1100以上になる確率を計算して、%表記で表示させます。

from scipy.stats import binom
print("probability: {:.8%}".format(1 - binom.cdf(1099, 2000, 0.5)))

計算結果は以下のように表示されます。当然ですがExcelで計算した場合と同じ結果になっています。

Console

probability: 0.00042285%

もっと単純に裏が900回以下になる確率を計算して以下のように書いてもいいです。
ライブラリの読み込みを忘れるとエラーになるので注意しましょう。

from scipy.stats import binom
binom.cdf(900, 2000, 0.5)

今回はformatを指定しなかったので、指数表記で結果が表示されます。

Console

4.228544767756799e-06

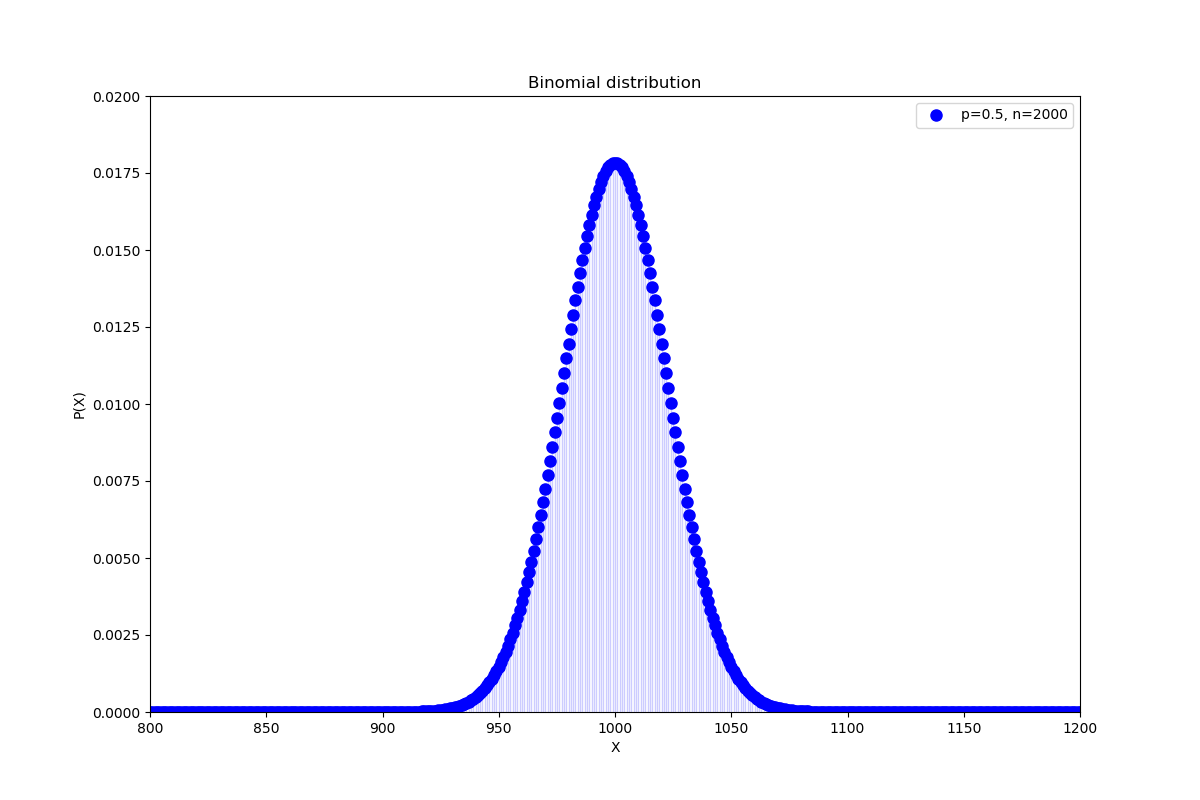
せっかくなのでbinom関数を使って二項分布のグラフを描いてみましょう。

binom_test.py

import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt

n = 2000
p = 0.5
x = np.arange(0, 2001)

fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x, binom.pmf(x, n, p), "bo", ms=8, label="p=0.5, n=2000")
ax.vlines(x, 0, binom.pmf(x, n, p), colors="b", lw=1, alpha=0.2)
ax.set_xlim(800, 1200)
ax.set_ylim(0, 0.02)

plt.xlabel("X")
plt.ylabel("P(X)")
plt.title("Binomial distribution")
plt.legend()
plt.show()

ほとんどの場合は950～1050の間におさまり、1100回以上起きる確率は極めて低い様子が視覚的にわかります。

###Rの場合

Rの場合はbinomは組み込み関数で、そのまま使用できます。
今回の確率を計算するには以下のように値を指定します。

pbinom(q = 1099, size = 2000, prob = 0.5, FALSE)

Console

4.228545e-06

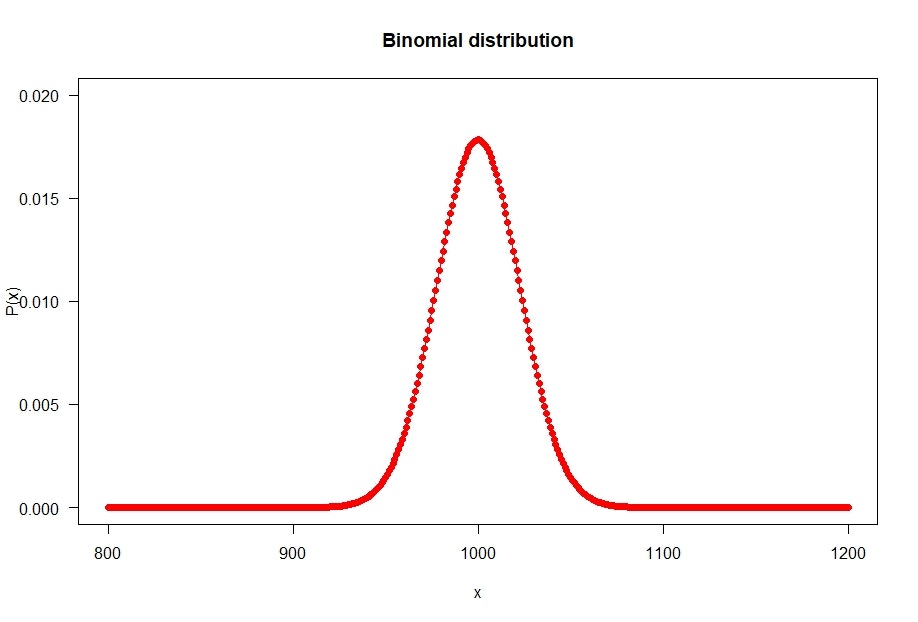
今回も二項分布をグラフにしてみます。

binomial_test.R

par(las=1)
n <- 2000
x <- seq(800, 1200)
plot (x, dbinom(x, n, 0.5), type = "o", col = "red", pch=16,
      ylab = "P(x)", main="Binomial distribution",
      xlim=c(800,1200), ylim=c(0,0.02))

###まとめ

2000回のコインで1100回以上というのは、直感的にはそれなりにあっても良さそうに感じてしまいます。
しかし実際は極めて低い確率になります。

Twitterのクイズでは10%以上と答えた人が最多で、正しい選択肢を選んだ人は一番少なかったです。
もしかすると10%と答えた人は、ポーカープレイヤーが多いかもしれません。
なぜならポーカーの分散に慣れていると、これくらいは平気で分散しそうに感じてしまうからです。

しかし、実際はポーカーの分散がおかしいのです。
100ハンドあたりの成績の期待値が4bb/100程度に対して、標準偏差が80bb/100とか、そういうゲームですからね。
期待値に比べて標準偏差が異常に大きすぎます。

いかがだったでしょうか。
今回の記事を通じて、確率の面白さを感じていただければ幸いです。

ご質問、必要な訂正箇所などあればコメントお願いします！

###補足
正規分布での確率を表ではなく、プログラムを使ってより正確に計算してみます。

from scipy.stats import norm
1 - norm.cdf(1100, 1000, 500 ** 0.5)

Console

3.8721082155079856e-06

1100以上になる確率は0.00038%になりました。
n = 2000では正規分布は二項分布とほぼ一致する程度に近似されていそうですが、どうして厳密に求めた値(0.00042285%)から誤差が生じるのでしょうか。

大きな理由は、正規分布は連続型確率分布で、二項分布は離散型確率分布だからです。
二項分布では整数の値しか取らずコインの表が出る回数が1100.1回になったりはしません。
正規分布に近似して考えるときには、この点に十分注意する必要があります。

正規分布にて以下のように計算すると、厳密な値にやや近づきます。

from scipy.stats import norm
1 - norm.cdf(1099.5, 1000, 500 ** 0.5)

Console

4.298009369074762e-06