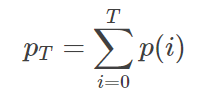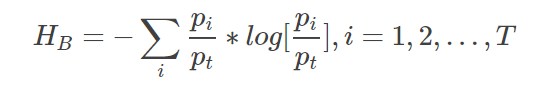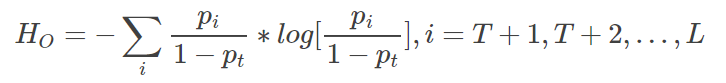OpenCV-最大エントロピー

1.最大エントロピーとは

ここでいうエントロピーとは、システムに含まれる情報のメトリックである情報エントロピーを指す。システムの不確実性が大きいほど,システムの情報エントロピーが大きくなる。逆に,1つのシステムが決定性が高い(システムが秩序化されているほど)場合,システム全体の情報エントロピーは小さくなる。その数学的定義は以下の通りである：

H=−∫p(x)log[p(x)]dx 

上記式では、p(x)は階調xが現れる頻度を表す。Hは情報エントロピーを表す。

2.最大エントロピー画像分割

1.1つの閾値Tを選択し、この閾値を用いて画像中の全ての画素点を2つに分類する，閾値T未満の全ての画素を背景Bとし、閾値T以上の全ての画素を物体Oとする。

2.各階調がBまたはOクラスに占める確率を計算する。

背景：    pi/pT,     i=1,2,...,T
物体:     pi/(1−pT), i=T+1,T+2,...,L

内に

3.背景と物体の情報エントロピーをそれぞれ計算する

4.画像の各階調について演算を行い、max（HO＋HB）を最大エントロピーの分割点とするT値を得る

3.OpenCVプラットフォームで実現

for (int i = 0; i < 256; i++) 
{
    //背景ピクセル数の計算
    double backTotal = 0;
    for (int j = 0; j < i; j++)
    {
        backTotal += tbHist[j];
    }

    //背景エントロピー
    for (int j = 0; j < i; j++)
    {
        if (tbHist[j] != 0)
        {
            Property = tbHist[j] / backTotal;
            backEntropy += -Property * logf((float)Property);
        }
    }
    //ぜんめんエントロピー
    for (int k = i; k < 256; k++)
    {
        if (tbHist[k] != 0)
        {
            Property = tbHist[k] / (TotalPixel - backTotal);
            frontEntropy += -Property * logf((float)Property);
        }
    }

    if (frontEntropy + backEntropy > maxEntropy)    //最大エントロピーを得る
    {
        maxEntropy = frontEntropy + backEntropy;
        index = i;
    }
    //今回の計算エントロピー値をクリア
    frontEntropy = 0.0;
    backEntropy = 0.0;
}