MATLABによるマルチエージェント合意制御 差分法・微分法による(コード)

こんにちは。初投稿です。
いつも興味深く皆さんの記事を拝見しているのですが、今回個人的にやっていたことが「ここに書いてもいいかもしれない」と思ったので、公開してみました。
Markdownにそもそも慣れてないんですが、どうぞ寛大なお心でご覧いただければと思います。

……と思って書いていたら重くて長くて仕方ないので、事前準備編/コード編で分けて公開しようと思います。ここはコード編です。
事前準備編はこちら→差分法・微分法の準備

3. シミュレーションのコード

それでは大変お待たせしました。ここからが本題のプログラムです。2.4の(1-9)・(1-10)式に示した差分方程式での実行例と、(1-1)・(1-2)式に示した微分方程式での実行例を比較してみましょう。
なお、以下はMATLAB 2022aで動作確認を行っています。多分これより前のバージョンでも大丈夫だと思います(3.1のところのlaplacianとかが微妙かも？)

3.1 下準備

まずは下準備として、処理の前に必要な変数などを定義しておきます。なお以降では同じプログラムの内容を分割して記述します(うまくコピペしてください)。

SabunBibun.m

clearvars
close all
%%%%%%%%%%%%% 基本設定 %%%%%%%%%%%%%
% シミュレーション領域
fx=10; fy=10;
% シミュレーション時間、サンプリング周期
tend=10; ts=1e-4;
% エージェントの台数
n=10;
%%%%%%%%%%%%% グラフによるエージェント同士の関係性の表現 %%%%%%%%%%%%%
% 隣接行列
gA=ones(n)-diag(ones(n,1));
% 各頂点に名前を付ける
gNames="Age "+num2str((1:n)');
% 隣接行列と名前を元にグラフを作る
gG=graph(gA~=0,gNames);
% 確認のためにグラフを表示
figure(10)
plot(gG)
% グラフラプラシアンの作成
gL=laplacian(gG);
%%%%%%%%%%%%% 後で使用する変数の定義 %%%%%%%%%%%%%
% 後々使う乱数のシード値
seed=123; rng(seed);

ここまでで下準備です。適当に変数名を付けてますがご容赦ください。

3.2 差分方程式の場合

この時のコードを示します。

SabunBibun.m

% 実行時間を計測
tBeginS=tic;

% 位置
rng(seed)
x_sab=fx*rand(n,1);
y_sab=fy*rand(n,1);

% 入力は最初は0
ux=zeros(n,1);
uy=zeros(n,1);

% 保存(出力)用の変数
memx_sub=zeros(n,tend/ts);
memy_sub=zeros(n,tend/ts);
memux_sub=zeros(n,tend/ts);
memuy_sub=zeros(n,tend/ts);

% 処理の実行
for k=1:tend/ts
    % 値の保存
    memx_sub(:,k)=x_sab;
    memy_sub(:,k)=y_sab;
    memux_sub(:,k)=ux;
    memuy_sub(:,k)=uy;
    % 入力の導出
    ux=-gL*x_sab;
    uy=-gL*y_sab;
    % 入力を基にした位置の更新
    x_sab=x_sab+ux*ts;
    y_sab=y_sab+uy*ts;
    % スパース処理
    x_sab(x_sab<0)=fx;
    x_sab(x_sab>fx)=0;
    y_sab(y_sab<0)=fy;
    y_sab(y_sab>fy)=0;
    % 簡単のため、小数点以下4桁くらいで四捨五入して0なら終了する
    if all(round(ux,4)==0) && all(round(uy,4)==0)
        % 逆算だけど、ここから「収束した」時刻を求めておく
        tconv=k*ts;
        break
    end    
end
if k<=tend/ts
    memx_sub(:,k+1:end)=[];
    memy_sub(:,k+1:end)=[];
    memux_sub(:,k+1:end)=[];
    memuy_sub(:,k+1:end)=[];
end

% 実行時間の表示
toc(tBeginS);

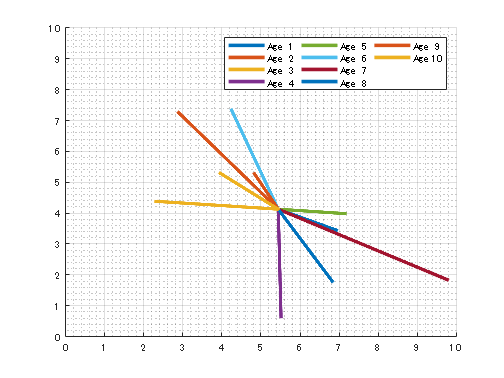
% 移動軌跡の表示
% 画像の番号
k=seed*100;

figure(k)
hold on
for kk=1:n
    plot(memx_sub(kk,:),memy_sub(kk,:),'LineWidth',3)
end
axis([0 fx 0 fy])
setLegGrid(n)

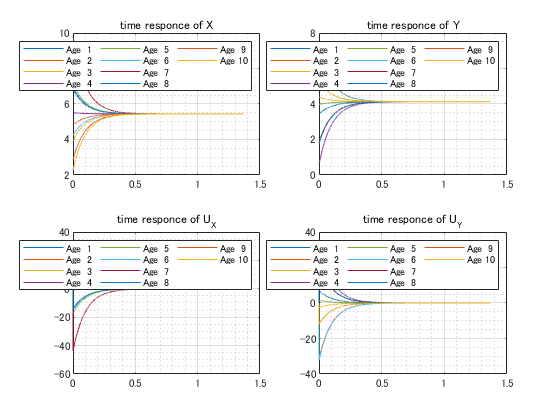
% 位置や入力の時刻歴応答の表示
figure(k+1)
subplot(2,2,1)
plot((1:length(memx_sub))*ts,memx_sub)
setLegGrid(n)
title("time responce of X")

subplot(2,2,2)
plot((1:length(memy_sub))*ts,memy_sub)
setLegGrid(n)
title("time responce of Y")

subplot(2,2,3)
plot((1:length(memux_sub))*ts,memux_sub)
setLegGrid(n)
title("time responce of U_X")

subplot(2,2,4)
plot((1:length(memuy_sub))*ts,memuy_sub)
setLegGrid(n)
title("time responce of U_Y")

結果はこんな感じ。

3.3 微分方程式の場合

ここが本題です(私としては)。本当にMATLAB様様Symbolic Math Toolbox様様なんですが、コマンド一発で出来ます。

SabunBibun.m

% 実行時間を計測する
tBeginB=tic;

% 初期位置
rng(seed)
x0_bibun=fx*rand(n,1);
y0_bibun=fy*rand(n,1);

% 数式で計算するので関数symsを使う。これ用の変数を定義。
syms x(t) [n,1]
syms y(t) [n,1]

% 時間の変数であるx,yという変数について
% "dQ/dt=-L*Q" (Q=x,y/L=gl=gL)という微分方程式を定義
odeX=(diff(x(t),t)==full(-gL)*x(t));
odeY=(diff(y(t),t)==full(-gL)*y(t));

% この方程式について、各x,yの初期値が上で求めたx0,y0である
% という条件式を代入する。
condX=(x(0)==x0_bibun);
condY=(y(0)==y0_bibun);

% この"odeQ"の方程式を"condQ"という初期値の下で解く。
% (Q=x,y) 何だか知らんがこれ一発で解ける。MATLABスゲー……
solX=dsolve(odeX,condX);
solY=dsolve(odeY,condY);

% よくわかんないけど結果がエージェント2からになる
% (何故か"x2","y2"からはじまる)のでこれを並び替える
solX=orderfields(solX,"x"+(1:10)');
solY=orderfields(solY,"y"+(1:10)');

% 実行時間の表示
toc(tBeginB);

k=seed*1000;
figure(k)
hold on
nameX=fieldnames(solX);
nameY=fieldnames(solY);

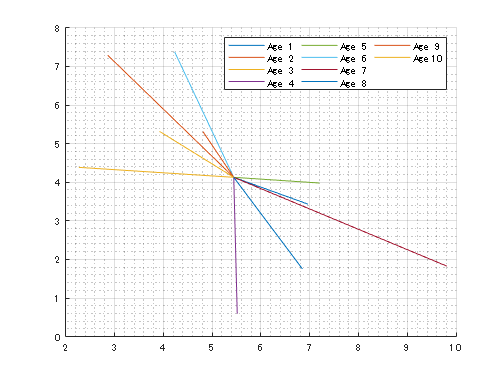
% 関数の名前を使って"fplot"によって「関数をプロット」する
% 今、各エージェントの位置が時間の関数として求まっているので
% 「これを0~tend秒までで実行し、その結果をプロットする」ようなイメージ
for kk=1:n
    % 実際に表示
    fplot(solX.(nameX{kk}(1,:)),solY.(nameY{kk}(1,:)),[0,tconv])
end

setLegGrid(n)

figure(k+1)
subplot(2,2,1)
hold on
for kk=1:n
    fplot(solX.(nameX{kk}(1,:)),[0,tconv])
end
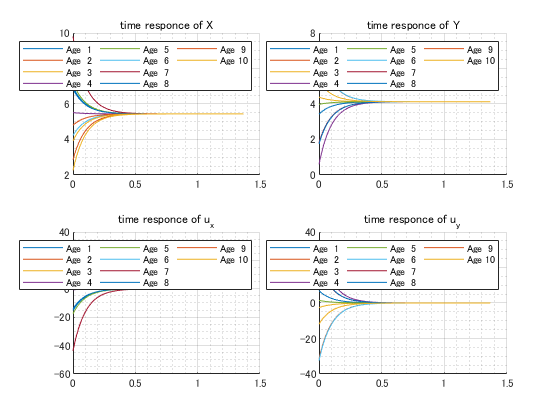
title("time responce of X")
setLegGrid(n)

subplot(2,2,2)
hold on
for kk=1:n
    fplot(solY.(nameY{kk}(1,:)),[0,tconv])
end
title("time responce of Y")
setLegGrid(n)

% 入力の数式を定義する
ux_bibun=(full(-gL)*subs(x(t),solX));
uy_bibun=(full(-gL)*subs(y(t),solY));

subplot(2,2,3)
hold on
for kk=1:n
    fplot(ux_bibun(kk),[0,tconv])
end
title("time responce of u_x")
setLegGrid(n)

subplot(2,2,4)
hold on
for kk=1:n
    fplot(uy_bibun(kk),[0,tconv])
end
title("time responce of u_y")
setLegGrid(n)

結果はこんな感じ。

3.4 付け足し(ファイル内関数)

実は何の断りもなく次に示す自作の入れ子関数？を使っています。ぶっちゃけ繰り返し書くのがめんどかった、というだけです。
ここまでコピペしてください。

SabunBibun.m

  function setLegGrid(n)
        legend("Age "+num2str((1:n)'),'NumColumns',round(n/3));
        grid on
        grid minor
    end

4. 結論

結果的に、微分方程式での結果も差分方程式の結果も同じになりました。微分方程式が一発で解けるのはすごいし、差分の方もサンプリング周期を小さくしていたので、当然と言えば当然ですね。

バチバチに趣味でごちゃごちゃやったのでこうして公開してみたんですが、問題ないはずです。何か不備などあればご教示ください。
MathWorksさん、今後ともよろしくお願いします。

参考文献

桜間 一徳, マルチエージェントシステムの制御 : III 合意制御(1), システム／制御／情報, 2013, 57 巻, 9 号, p. 386-396