多目的進化型アルゴリズムMOEA/Dとその改良手法

はじめに

世の中には、複数の目的を持った最適化問題が存在します。例えば、高性能な車のエンジンを開発したい場合、燃費を良くしたい、重量を軽くしたい、サイズを小さくしたい、といった複数の目的がありえます。こういった問題を解く方法として、それぞれの目的別に単目的で最適化する、という方法もありますが、それではちょうどいい解（燃費、重量、サイズがそれぞれ一番良くはないけれど、そこそこのバランスが取れている解）が得られません。

そこで登場するのが多目的最適化アルゴリズムです。多目的最適化アルゴリズムは、複数の目的を考慮した上で、最適な解集合を獲得することを目的としています。この記事では、進化計算を多目的最適化に応用した手法であるMOEA/D（A Multiobjective Evolutional Algorithm based on Decomposition）を紹介します。

ただし、私自身進化計算を追っていたのは数年前のため、情報が古い可能性があります・・・。ご了承ください。

多目的最適化

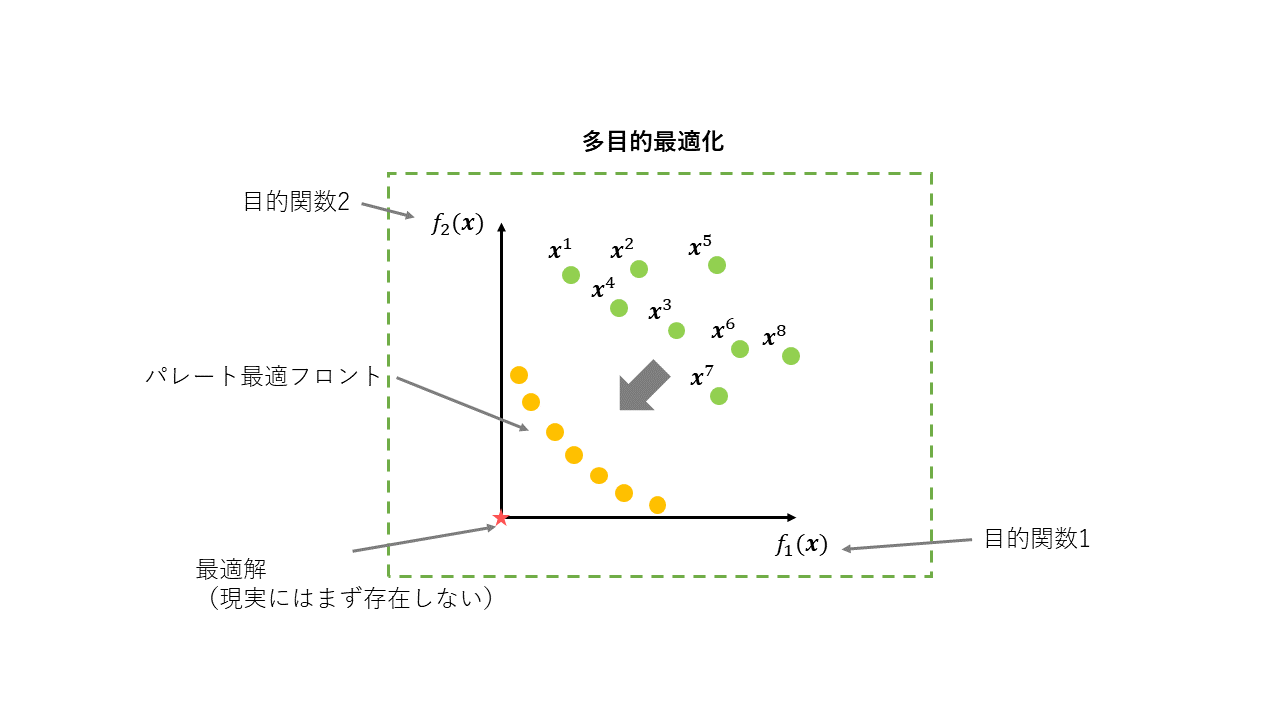
はじめに、多目的最適化について簡単に説明します。多目的最適化はその名の通り、複数の目的を持つ最適化問題です。
定義などは検索すればすぐ出てくるため省略しますが、図解すると以下のような問題と言えます。

最適解は一見、図中の星の位置に見えますが、実問題でこの最適解はほぼ存在しません。なぜなら、多くの問題は各目的関数にトレードオフ（あちらが立てばこちらが立たず）の関係を持っているためです。

その場合、最適解は複数（問題によっては無限個）存在することになります。上図中のオレンジの点です。この最適解集合をパレート最適フロント（Pareto Optimal Front）と呼び、基本的にはこのパレート最適フロントを求めることが多目的最適化の目的です。

MOEA/D（A Multiobjective Evolutional Algorithm based on Decomposition）

MOEA/Dは、Zhang、Liらによって2007年¹に提案された、多目的問題をスカラー化関数によって複数の単目的問題に分割して解く手法です。

ここでは、数式をなるべく使わずにMOEA/Dの大体のニュアンスを説明したいと思います。

MOEA/Dの流れ

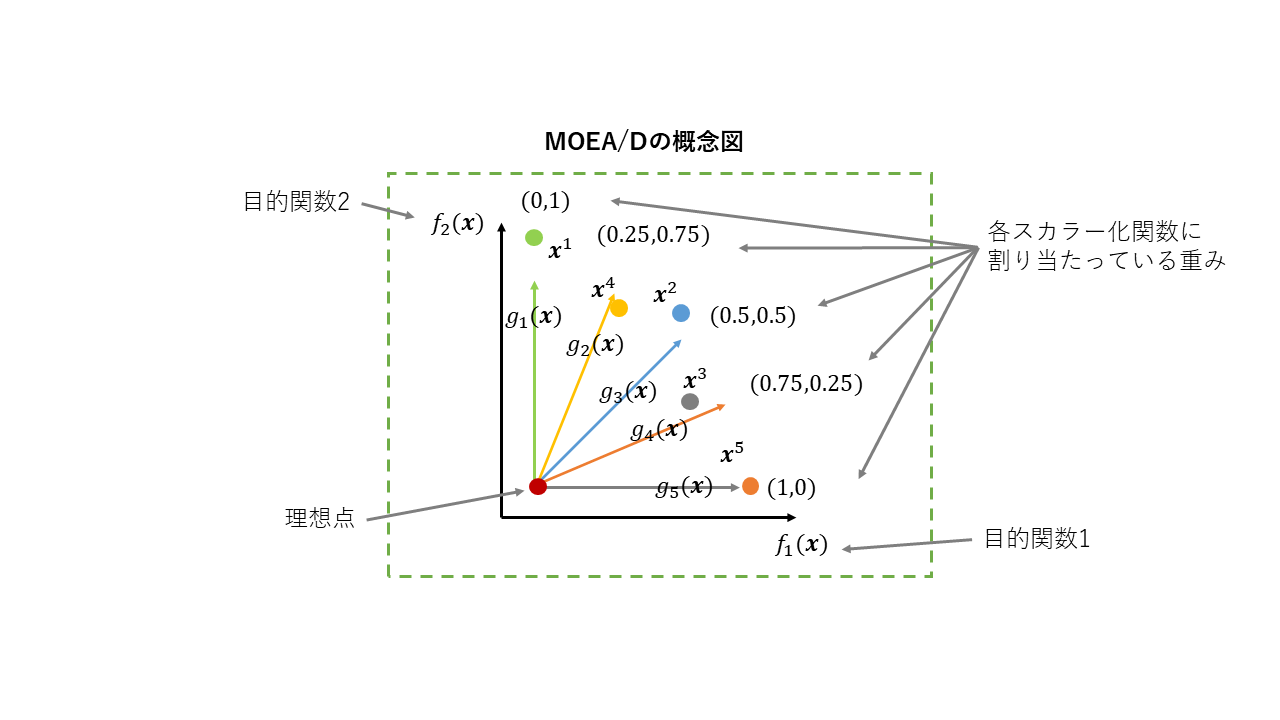
MOEA/Dでは、初期個体群をそれぞれ別のスカラー化関数に割り当て、個体$\boldsymbol{x}^1$は$f_1(\boldsymbol{x})$よりの方向、個体$\boldsymbol{x}^2$は$f_2(\boldsymbol{x})$よりの方向、というように個体毎に探索する方向を変えてやることで、均一なパレートフロントの獲得を目指します。

MOEA/Dの概念図は以下です。

※上記の図は設計変数空間ではなく、目的空間を表していることに注意してください

図中の$g$が部分問題（スカラー化関数）であり、各部分問題にはそれぞれ別の重みベクトルが割り当たっています。例えば重みベクトル(1,0)が割り当たっているスカラー化関数は$f_1(\boldsymbol{x})$に対する重みが1、$f_2(\boldsymbol{x})$に対する重みが0となるため、$f_2(\boldsymbol{x})$を無視して$f_1(\boldsymbol{x})$方向への探索を行います。

ここで、スカラー化関数は以下のような種類があります。

• Weighted Sum
  
• Tchebycheff
  
• Achevement Scalarizing Function (ASF)
  
• Penalty-based Boundary Intersection (PBI)
  
• Inverted Penalty-based Boundary Intersection (IPBI)
  

最もシンプルなスカラー化関数はWeighted Sumです。これは、各目的関数値に重み付けた値の合計をスカラー化関数値とするものです。

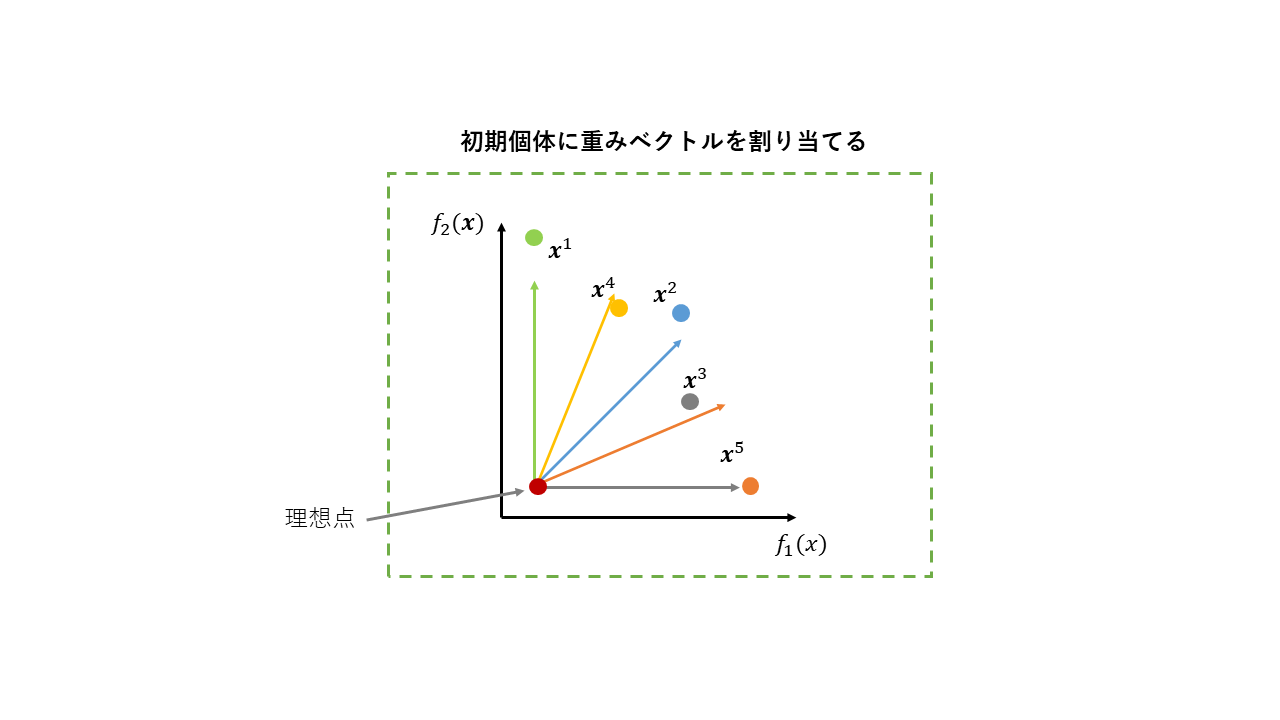
1. 初期化

初期個体（緑の丸）をランダムに生成し、ランダムに重みベクトルを割り当てます。今回の例では、二つの目的関数をもつ問題の最適化をします。

この時、全個体中から各目的関数における最小値を理想点として設定します。

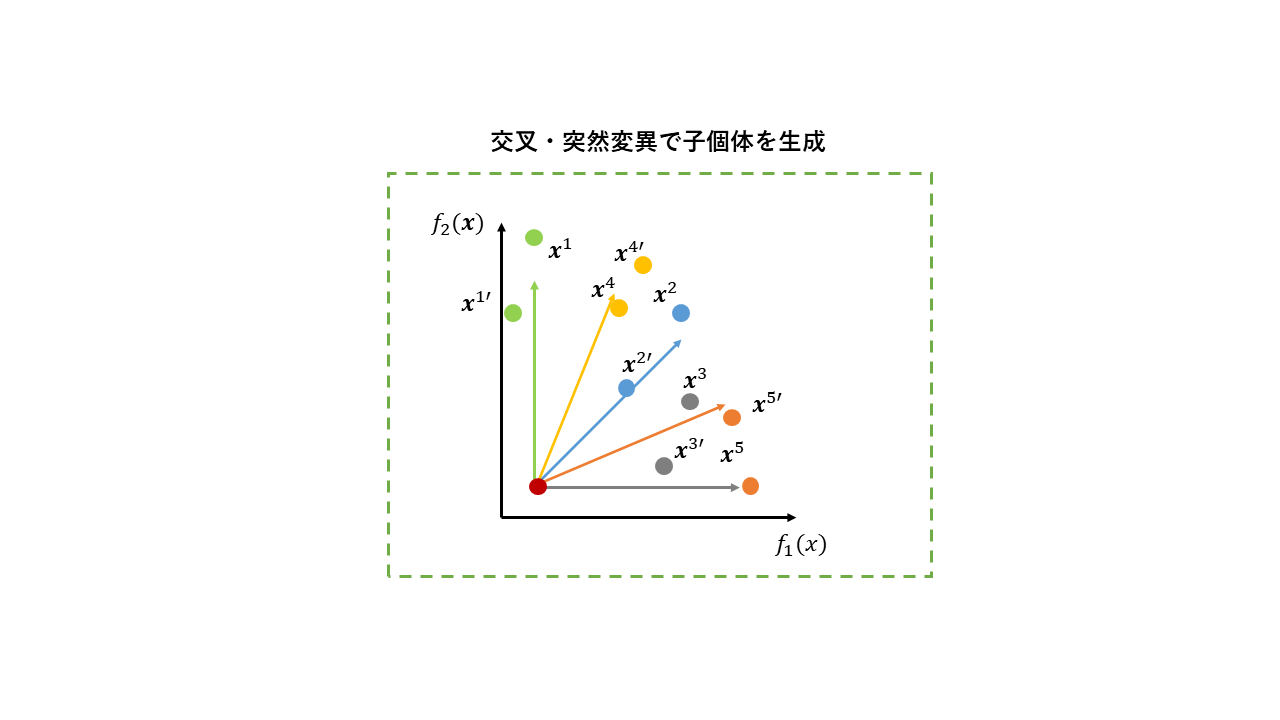
2. 交叉・突然変異

交叉・突然変異を行って子個体を生成します。交叉対象の親個体は近傍（ユークリッド距離が近い重みベクトルに割り当たっている個体）から選択します。

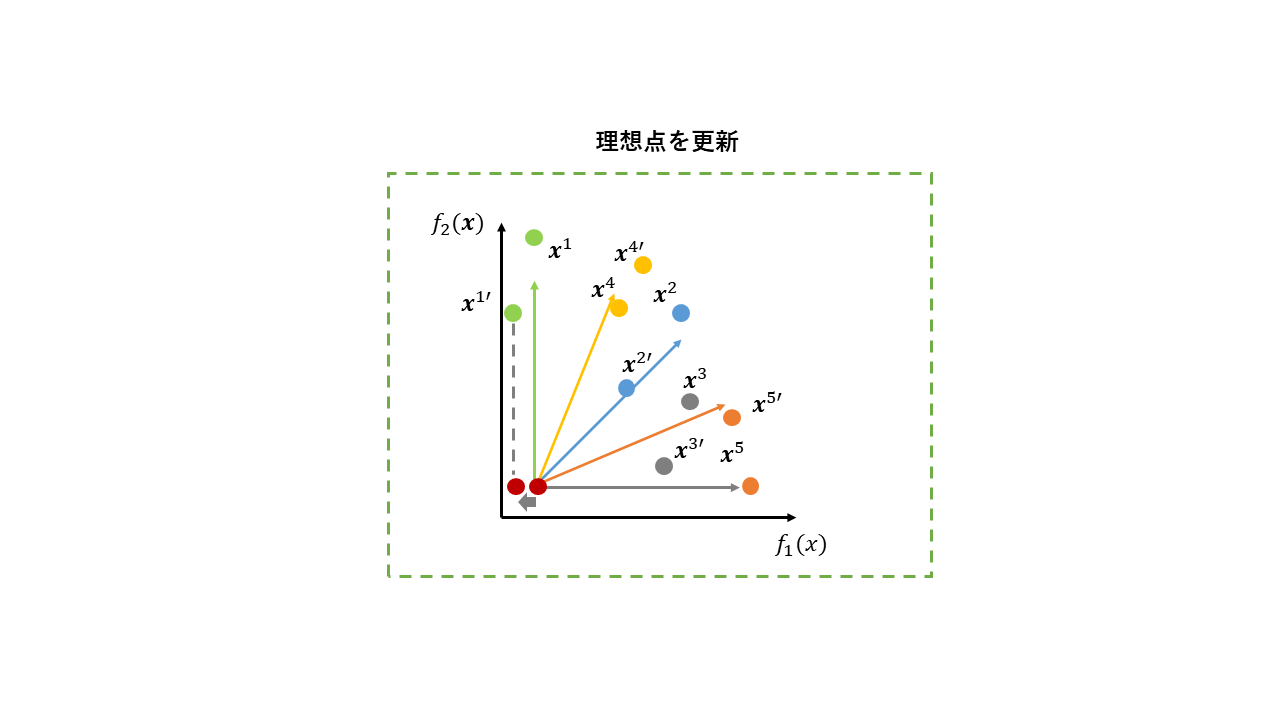
3. 理想点の更新

生成した子個体を利用して、理想点を更新します。子個体が全て現個体の劣解だった場合、理想点の更新は行われません。

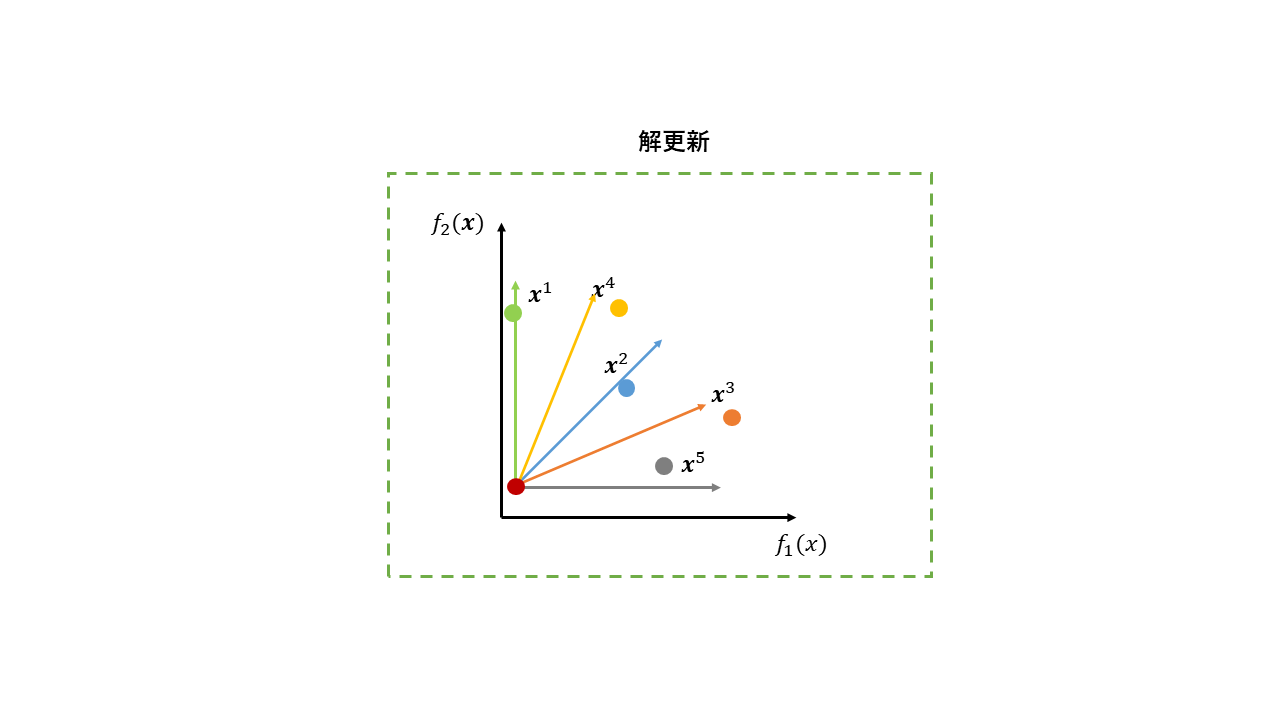
4. 解の更新

親個体と子個体を比較し、優れている方を残します。この時、あくまで比較はスカラー化関数の値で行うため、初期化時にはランダムだった解集合は、徐々に割り当たっている重みに近い方向へと探索を進めていきます。

5. 終了判定

終了条件を満たすまで2~4を繰り返します。これらを繰り返すことで、良質な個体を次世代に残し、探索を進めていきます。一般的に、終了条件には世代数（繰り返し回数）が設定されます。

MOEA/Dの改良版

MOEA/Dは界隈では非常にメジャーなため、改良アルゴリズムはいくつも提案されています。その中で有名っぽいものをいくつかコンセプトだけ紹介します。

MOEA/D-DE²

MOEA/Dの交叉にDE（Differential Evolution）の突然変異を使用し、性能向上したアルゴリズムです。また、交叉する親個体を選択する際に、常に近傍から選択するのではなく、確率的に近傍外からも選択するようにすることで多様性が失われることを防いでいます。

MOEA/D-DRA³

MOEA/D with Dynamical Resource Allocationの名の通り、毎世代の改更新の際に、有望な（より探索の進んでいる）部分問題に絞って探索を進めるアルゴリズムです。

ベースはMOEA/D-DEですが、各部分問題にパラメータπを保持している点が異なります。世代終了時に、スカラー化関数の更新度合いに応じてπの値を変化（更新度合いが一定より少なければπを小さくしていく）させ、親個体選択時にはπを基に10-トーナメント選択で遺伝的操作を行う親個体を選択します。

おわりに

おそらく、今はもっと色々なアルゴリズムが出ていると思います。現状がどうなっているかわかりませんが、活用が進んでいると良いですね。

---

1. Q. Zhang and H. Li, "MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition," in IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712-731, Dec. 2007, doi: 10.1109/TEVC.2007.892759. ↩

2. H. Li and Q. Zhang, "Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II," in IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 284-302, April 2009, doi: 10.1109/TEVC.2008.925798. ↩

3. Zhang, Qingfu & Liu, Wudong. (2009). The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. 2009 IEEE Congress on Evolutionary Computation, CEC 2009. 203 - 208. 10.1109/CEC.2009.4982949.  ↩