始めに
これまで様々な関数が出てきました。損失関数や最適化関数といったモノたち、強敵でしたがここまで来たあなたなら次の関数も分かるはず!
なんと今回の関数でAIに使われている関数の紹介が終わります。
そして、今回解説する関数は……活性化関数です!
活性化関数は損失関数や最適化関数とは比べ物にならないほど数があるため、今回は代表的な関数を4つ解説していきます。
では、たくさんあるとされている活性化関数とはいったい何でしょうか?
一言でいうと、活性化関数とは各層の出力の前に使うことで、値を最適化することができる関数です。
イメージとしては、フィルターの役割に似ています。
sigmoid関数
f(x) = \frac{1}{1+e^{-x}}
sigmoid関数は、値を必ず1から0の間に変換することのできる関数です。
値が必ず0~1の間になるということは、その値を確立としてみなすことができます。
これらの特性を生かして、主に二値分類の最終層に使われたりします。
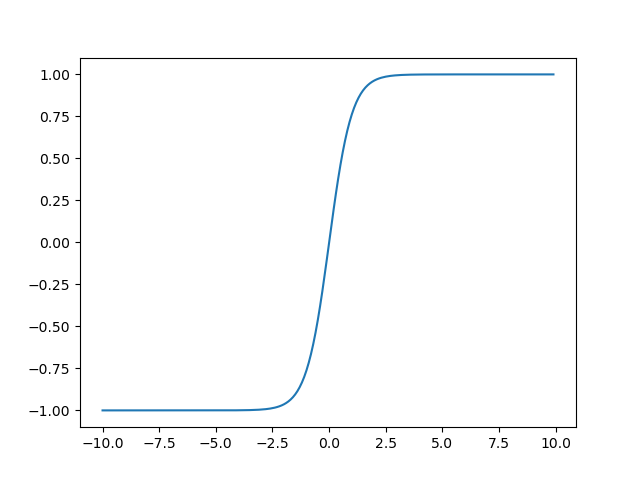
Tanh関数
f(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}
Tanh(ハイパボリックタンジェント)関数は、値を必ず1から-1の間に変換することのできる関数です。
また、Sigmoid関数では値の変動が0~1までの間しかないため微分係数を求めた際の最大値が0.25しかなく、なかなか学習が進まない問題がありましたが、Tanhの場合は微分係数の最大値が1となり、学習を進めやすくすることができるようになりました。
ReLu関数
f(x) = \left\{
\begin{array}{ll}
x & (x > 0) \\
0 & (X \leq 0)
\end{array}
\right.
ReLU(レクティファイドリニアユニットまたはランプ)関数は、値がマイナス域の場合は0を出力し、プラス域の場合はそのまま出力する関数です。
この特徴を生かして、マイナスの値があると不都合となる問題(画像に関わる問題など)に使用されることが多いです。
Softmax関数
f(x) = \frac{\exp(a_x)}{\sum_{i=1}^a exp(a_i)}
softmax関数は、入力された項目毎に出力される値が変わり、それらすべての値を足し合わせると必ず1になるようにな関数です。
softmax関数は今回紹介する中で一番数式が複雑です。注意点として、softmax関数のみ入力された値に応じてグラフの形も変わります。
また、すべての値は必ず0~1の間(確率)になります。
終わりに
これであなたも関数マスターです!
え?実感がわかないって?
ならば試しに、道行く少女に関数の説明をしてみなさい。
さすればあっという間に通報されることでしょう。
記事作成:Y&N