この記事ではずっとやってみたかった量子テレポーテーションという現象を Qiskit にて実装してみたいと思います。
量子テレポーテーションとは
量子テレポーテーションとはざっくりというと
ある量子状態を (遠く) 離れた場所に転送することです。
例えばアリスさんが量子状態 $|\psi\rangle$ を持っていた場合、
遠く離れたボブさんにアリスさんが $|\psi\rangle$ を転送するといったことが量子テレポーテーションです
また、量子テレポーテーションを行うと転送元にあった量子状態はなくなります。
一般的なコンピュータではあるビットの状態を複製し、どこかへ転送することができるので、量子コンピュータでもそのようにすれば転送できそうですが、そのようなことができません。
量子複製不可能定理というものがあり、ある未知な量子状態を複製すること不可能なのです。
このことは、量子の世界と古典的なマクロな世界の大きな違いとなっています。
実行環境など
量子テレポーテーションを実装するにあたり、Qikit という IBM が開発した SDK を利用します。Swift や JavaScript でも書けるらしいのですが、Python で書くことにします。
実行環境は次の通りです。
- Anaconda
- Jupyter Notebook
- python:3.10.9
- qiskit:0.41.1
理論編
量子テレポーテーションについていろいろと読んでいたところ、
個人的には理論を聞いてから、実装方法を見るほうがわかりやすいと感じたのでこの記事ではそのように説明をします。
冒頭でも記載したようにある量子状態を (遠く) 離れた場所に転送するのが量子テレポーテーションです。
その転送したい量子状態を
|\psi\rangle = \alpha|0\rangle + \beta|0\rangle
とします。
ここで、アリスさんが $|\psi\rangle$ を遠く離れたボブさんに転送したいと仮定して話を進めます。
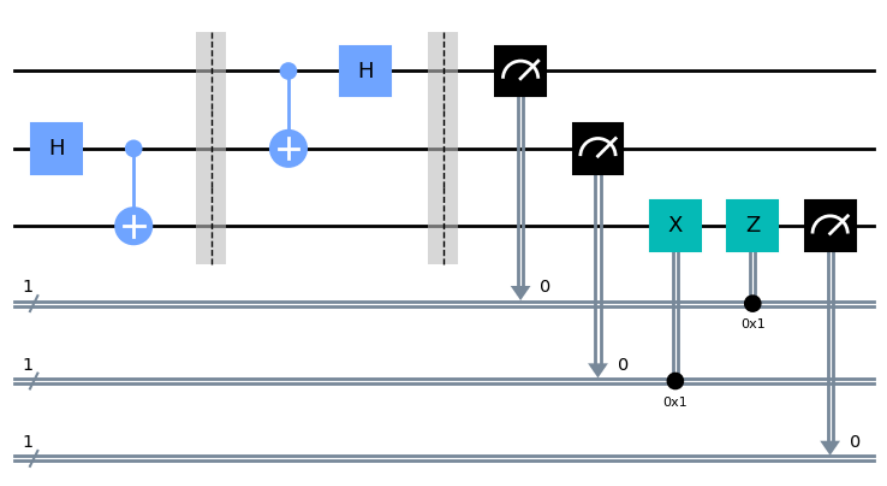
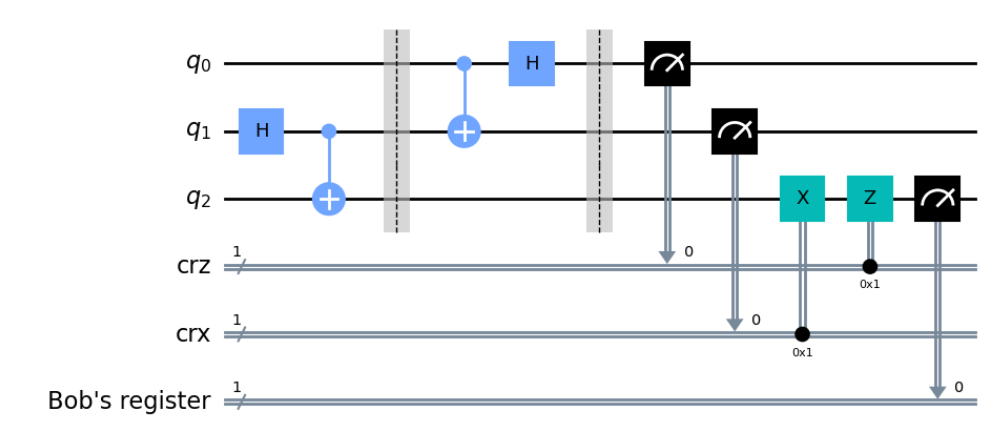
量子テレポーテーションを実行するための量子回路図は以下のようなものです。
まず初めに、$|q_0\rangle$ と $|q_1\rangle$ をアダマールゲートと CNOT ゲートによって量子もつれ状態にします。すると、次のようになります。
|q_0\rangle|q_1\rangle = \frac{1}{\sqrt{2}}(|0\rangle|0\rangle + |1\rangle|1\rangle)
その後、もつれさせた $|q_0\rangle$ と $|q_1\rangle$ のうち、一つをアリスさんに渡しもう一つをボブへと渡します。ここでは、$|q_0\rangle$ をアリスさんに渡し、$|q_1\rangle$ を遠く離れたボブさんに渡すとして話を進めます。
もつれさせた量子ビットを二人に渡したら、次はアリスさんが持っている $|q_0\rangle$ と転送を行いたい $|\psi\rangle$ に対して、 CNOT ゲートを通し、H ゲートを作用させます。CNOT ゲートを通す前と通した後は次のように書くことができます。作用させる CNOT は $|\psi\rangle$ を制御量子ビット、$|q_0\rangle$ をターゲット量子ビットとしていますので、$|\psi\rangle$ が $|1\rangle$ のときに、$|q_0\rangle$ の量子ビットを反転させます。
\begin{align}
&|\psi\rangle|q_0\rangle|q_1\rangle = (\alpha|0\rangle + \beta|1\rangle)\frac{1}{\sqrt{2}}(|0\rangle|0\rangle + |1\rangle|1\rangle)\\
&= \frac{1}{\sqrt{2}}(\alpha|0\rangle|0\rangle|0\rangle + \alpha|0\rangle|1\rangle|1\rangle + \beta|1\rangle|0\rangle|0\rangle) + \beta|1\rangle|1\rangle|1\rangle) \\
&\xrightarrow{CNOT} \frac{1}{\sqrt{2}}(\alpha|0\rangle|0\rangle|0\rangle + \alpha|0\rangle|1\rangle|1\rangle + \beta|1\rangle|1\rangle|0\rangle) + \beta|1\rangle|0\rangle|1\rangle) \tag{1}
\end{align}
その後、H ゲートを作用させるのですが、ここで H ゲートがどういったものかを簡単に説明をしておきます。H ゲートは次のように表現することができます。
H = \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}
よって、H ゲートを $|0\rangle$ や $|1\rangle$ に作用させると次のようになります。
|0\rangle \xrightarrow{H} \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle) \\
|1\rangle \xrightarrow{H} \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle)
このことより、式(1) は H を作用させると次のようになります。
|\psi\rangle|q_0\rangle|q_1\rangle
= \frac{1}{2}\biggl\{\alpha\Bigl(|0\rangle + |1\rangle\Bigr)|0\rangle|0\rangle + \alpha\Bigl(|0\rangle + |1\rangle\Bigr)|1\rangle|1\rangle + \beta\Bigl(|0\rangle - |1\rangle\Bigr)|1\rangle|0\rangle) + \beta\Bigl(|0\rangle - |1\rangle\Bigr)|0\rangle|1\rangle\biggr\}
この式を展開して整理すると次のように書くことができます。
|\psi\rangle|q_0\rangle|q_1\rangle
= \frac{1}{2}\biggl\{|0\rangle|0\rangle(\alpha|0\rangle + \beta|1\rangle) + |0\rangle|1\rangle(\alpha|1\rangle + \beta|0\rangle) + |1\rangle|0\rangle(\alpha|0\rangle - \beta|1\rangle) + |1\rangle|1\rangle(\alpha|1\rangle - \beta\|0\rangle)\biggr\}
この式が意味していることはアリスさんの手元にある $|\psi\rangle|q_0\rangle$ を観測した結果、例えば $|0\rangle|0\rangle$ という観測結果を得たら、$|q_1\rangle$ は $\alpha|0\rangle + \beta|1\rangle$ という状態になっているということです。
つまり、アリスさんの観測結果によってボブさんが持っているビットの状態は次のように決まるということです。
|\psi\rangle|q_0\rangle \rightarrow |q_1\rangle \\
--------- \\
|0\rangle|0\rangle \rightarrow \alpha|0\rangle + \beta|1\rangle \\
|0\rangle|1\rangle \rightarrow \alpha|1\rangle + \beta|0\rangle \\
|1\rangle|0\rangle \rightarrow \alpha|0\rangle - \beta|1\rangle \\
|1\rangle|1\rangle \rightarrow \alpha|1\rangle - \beta\|0\rangle
ここまでわかったところで、もう一度量子テレポーテーションとは何だったかを確かめてみましょう。
量子テレポーテーションとは、アリスさんが持っている状態
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
をボブさんに転送することでした。
最後の結果を見てみると、アリスさんの手元になる $|\psi\rangle|q_0\rangle$ を観測した結果、 $|0\rangle|0\rangle$ であったら、アリスさんはボブさんに LINE で ボブさんが持っている量子ビットに何もしないで!と伝えておけばボブさんはもともとアリスさんが持っていた状態 $|\psi\rangle$ を持っていることになります。つまり、状態を転送できていることになります。
今度は、アリスさんの手元になる $|\psi\rangle|q_0\rangle$ を観測した結果、 $|0\rangle|1\rangle$ であった場合について考えてみます。この場合、ボブさんの量子ビットの状態は $\alpha|1\rangle + \beta|0\rangle$ になっています。ですので、この場合ボブさんに LINE で NOT を作用する、つまり X ゲートを作用するように伝えればボブさんは状態 $|\psi\rangle$ にすることができます。
同様に、$|\psi\rangle|q_0\rangle$ を観測した結果、 $|0\rangle|1\rangle$ であった場合は、ボブさんの量子ビットの状態は $\alpha|0\rangle - \beta|1\rangle$ になっていますので、180°の位相ゲート Z を作用させるように伝えればよいです。
また、$|\psi\rangle|q_0\rangle$ を観測した結果、 $|1\rangle|1\rangle$ であった場合は、ボブさんの量子ビットの状態は $\alpha|1\rangle - \beta|0\rangle$ になっていますので、NOT を作用させて180°の位相ゲートを作用させる、つまり Y ゲートを作用するように伝えればよいです。
まとめると次の表のようになります。
| $|\psi\rangle|q_0\rangle$ | ボブさんの量子ビットの状態 | 作用するゲート |
|---|---|---|
| $|0\rangle|0\rangle$ | $\alpha|0\rangle + \beta|1\rangle$ | I |
| $|0\rangle|1\rangle$ | $\alpha|1\rangle + \beta|0\rangle$ | X |
| $|1\rangle|0\rangle$ | $\alpha|0\rangle - \beta|1\rangle$ | Z |
| $|1\rangle|1\rangle$ | $\alpha|1\rangle - \beta|0\rangle$ | Y |
というように、アリスさんの観測結果をもとに、ボブさんに作用してほしいゲートを伝えれば状態 $|\psi\rangle$ を転送することができます。これが、量子テレポーテーションなのです。
実装
量子テレポーテーションについてわかったところで、実際に Qiskit を使って実装をしてみます。
ソースコード全体は次のようになります。
簡単のため、 $|0\rangle$ を転送するとしています。
import numpy as np
from numpy import pi
import matplotlib.pyplot as plt
%matplotlib inline
from qiskit import *
from qiskit.visualization import plot_histogram, plot_bloch_multivector, array_to_latex
# 量子レジスタと古典レジスタを準備
qr = QuantumRegister(3, name='q')
crz = ClassicalRegister(1, name='crz')
crx = ClassicalRegister(1, name='crx')
qc = QuantumCircuit(qr, crz, crx)
# q1 と q2 を量子もつれ状態とする
qc.h(1)
qc.cx(1, 2)
qc.barrier()
# 転送したいq0 と q1 について相互作用させる
qc.cx(0, 1)
qc.h(0)
qc.barrier()
# アリスさんが持っているq0 と q1 を測定する
qc.measure(0, 0)
qc.measure(1, 1)
# アリスさんの測定結果に応じてボブさん側で演算を行う
qc.x(2).c_if(crx, 1)
qc.z(2).c_if(crz, 1)
# ボブさんの持っている q2 を測定する
cr_result = ClassicalRegister(1, 'Bob\'s register')
qc.add_register(cr_result)
qc.measure(2, 2)
# 量子回路の描画処理
# qc.draw('mpl')
# シミュレータで測定し、結果を描画
backend = Aer.get_backend('aer_simulator')
results = execute(qc, backend=backend, shots=1024).result()
answer = results.get_counts()
plot_histogram(answer)
また、この時の量子回路図は、理論ところで書いたものと同様なものです。
※ わかりにくいかもしれませんが、量子ビットの名称が理論のところと少し異なっています。
各処理で何をしているか順に見ていきましょう。
まず、以下の部分では必要なモジュールのインポートと量子テレポーテーションに必要な量子レジスタと古典レジスタの準備をしています。
import numpy as np
from numpy import pi
import matplotlib.pyplot as plt
%matplotlib inline
from qiskit import *
from qiskit.visualization import plot_histogram, plot_bloch_multivector, array_to_latex
# 量子レジスタと古典レジスタを準備
qr = QuantumRegister(3, name='q')
crz = ClassicalRegister(1, name='crz')
crx = ClassicalRegister(1, name='crx')
qc = QuantumCircuit(qr, crz, crx)
次に、理論のところでお話ししましたが、二つの量子ビットを量子もつれ状態とさせます。
量子もつれにしたいので、H ゲートを作用させて CNOT ゲートを作用させるという処理が必要です。
# q1 と q2 を量子もつれ状態とする
qc.h(1)
qc.cx(1, 2)
量子もつれ状態にすることができたら、もつれさせた二つの量子ビットをアリスさんとボブさんにそれぞれ一つづつ渡して、ボブさんには遠くに離れてもらいます。
その後、アリスさんの方では、転送したい量子ビット $|q_0\rangle$ とアリスさんが持っている量子もつれ状態の $|q_1\rangle$に対して、CNOT ゲートを通し、H ゲートを作用させます。
# 転送したいq0 と q1 について相互作用させる
qc.cx(0, 1)
qc.h(0)
ボブさんにアリスさんの手元にある転送したい量子ビット $|q_0\rangle$ を転送するには、理論のところで述べた通り、アリスさんが持っている $|q_0\rangle$ と $|q_1\rangle$ を測定する必要があります。
その後、その測定結果に基づいて、ボブさん側でどういった操作をすればよいかをアリスさんは伝える必要があります。
例えば、$|q_0\rangle$ が 1 である場合は、ボブさんは X ゲートを作用させる必要があります。
以上のような処理は次の箇所で処理を行っていることになります。
c_if は古典レジスタの測定値に応じて、量子レジスタに指定した操作を行うようなものです。
qc.x(2).c_if(crx, 1) とありますが、これは crx の測定値が 1 である場合に、量子レジスタ $|q_2\rangle$ (ボブさんが持っているレジスタ) に X ゲートを作用させるということを意味しています。
# アリスさんが持っているq0 と q1 を測定する
qc.measure(0, 0)
qc.measure(1, 1)
# アリスさんの測定結果に応じてボブさん側で演算を行う
qc.x(2).c_if(crx, 1)
qc.z(2).c_if(crz, 1)
次の残りの部分では、ボブさん側で測定をし、結果を描画するという処理を行っています。
# ボブさんの持っている q2 を測定する
cr_result = ClassicalRegister(1, 'Bob\'s register')
qc.add_register(cr_result)
qc.measure(2, 2)
# 量子回路の描画処理
# qc.draw('mpl')
# シミュレータで測定し、結果を描画
backend = Aer.get_backend('aer_simulator')
results = execute(qc, backend=backend, shots=1024).result()
answer = results.get_counts()
plot_histogram(answer)
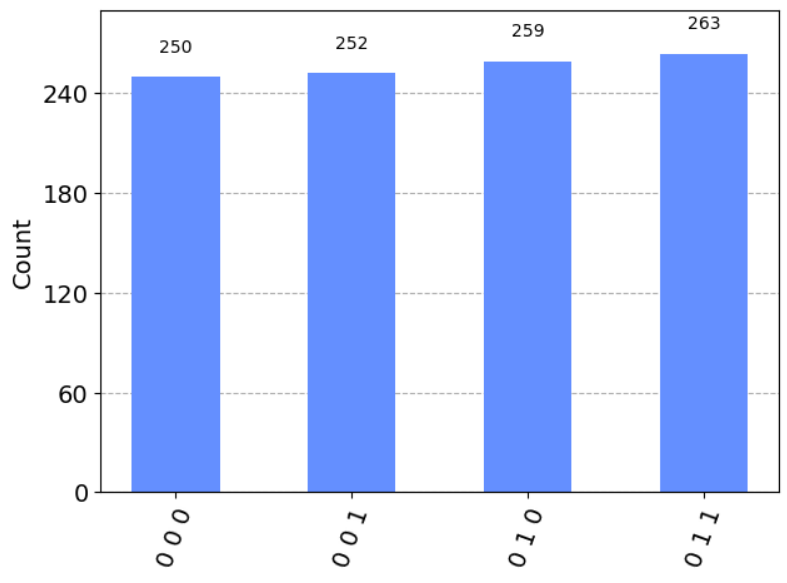
実行結果
上記のコードは 1024 回シミュレーションするというものになっているのですが、実行しますと次のようになります。縦軸がイベント数で、横軸が 3 つの古典ビットの値です。
結果を見てみますと、一番左のビットが必ず 0 になっていることがわかります。このビットに対応するのが、ボブさんが持っていたレジスタです。
よって、量子テレポーテーションによって、転送をしたかった $|0\rangle$ がボブさんに転送できました。
まとめ
大まかにですが、量子テレポーテーションの理論からシミュレーションまでやってみました。
転送する量子状態を $|0\rangle$ としましたが、一般的な量子状態で量子テレポーテーションをすることができます。興味があれば、好きな状態を作って転送をしてみてください!
参考文献
量子テレポーテーション - EMANの物理学
量子テレポーテーション - Qiskit
IBM Quantumで学ぶ量子コンピュータ
Qiskitで量子テレポーテーション!