量子コンピュータにおける Hello World プログラムは
Bell 状態というものを作り出すことに相当するようです。
この記事では、Bell 状態を作り出すことを目標として、なるべく定性的に説明を記述します。
Hello Worldの量子回路図 ( Bell状態 )
Hello Worldプログラムに相当する量子回路図は次の通りです。
赤色の「H」と書かれたものが、アダマールゲートというもので $|0\rangle$ または $|1\rangle$ をそれぞれ 50 % の確率で観測されるような重ね合わせ状態を作るものです。
詳しい説明は過去に量子コンピュータにおけるHello worldの一歩手前を理解するで記載しましたのでそちらを参照していただくか、多くの他の文献で説明がされていますのでそちらを見るとよいと思います。
また、二つの量子ビットにまたがる青い十字のものは、CNOT演算子と呼ばれるものでこちらについては以降で説明をします。
CNOT ゲート
アダマールゲートは1入力の量子演算子であったのに対して、CNOTゲートは2入力の量子演算子です。
CNOT ゲートがどういったものであるかを理解するために、その真理値表を見てみましょう。
そちらを見ると、Input1 が 0 のときは、入力した値がそのまま出力されますが、Input1 が 1 のときは、Input2 の値が反転されて Output2 として出力されることがわかるかと思います。
つまり、Input1 が 0 or 1 であるかによって、Input2 の値が反転されるか否かが決まるということになります。
Input1 は Input2 のビットを制御しているようにとらえることができるので、Input1 のことは制御量子ビットと呼ばれ、Input2 はビットの制御対象となっているので、Input2 のことはターゲット量子ビットと呼ばれます。
CNOT ゲートの真理値表
| Input1 | Input2 | Output1 | Output2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
また、CNOT ゲートは古典コンピュータでの XOR 演算子に対応する演算子となっています。
このことを確かめるために、XOR 演算子の真理値表を見てみます。
XOR 演算子の説明として、2入力のうちどちらか一方が 1 であればその出力は 1 となるといった説明をされることもあるかと思います。
しかしながら、この演算子を違う見方をすると、Input1 のビットが 1 であるときに、Input2 のビットを反転して出力する演算子と捉えることもできます。
このように捉えると、XOR 演算子と上で説明をした CNOT ゲートは似たようなものであり、CNOT ゲートは古典コンピュータでの XOR 演算子に対応すると考えることができるかと思います。
XOR 演算子の真理値表
| Input1 | Input2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
ここまでを簡単にまとめると
CNOT ゲートは制御量子ビットが 1 のときにターゲット量子ビットを反転させる。
CNOT ゲートは古典コンピュータでの XOR 演算子に対応する演算子である。
量子もつれと Bell 状態
さて、Hello Worldプログラムに相当する量子回路図で使用されているゲートについてすべて理解ができる状態となりました。ここからは、この量子回路図は何をすることになるのかを書いていきます。
順に処理を見ていくと、まず $|q_0\rangle$ に対してアダマールゲートがありますので、$|q_0\rangle$ は $|0\rangle$ or $|1\rangle$ の重ね合わせ状態になります。その後、$|q_1\rangle$ をターゲット量子ビットとする CNOT ゲートがあり、また $|q_1\rangle$ のビットの状態は $|0\rangle$ ですので、$H \rightarrow CNOT$ とすると下の真理値表からわかるように $|00\rangle$ or $|11\rangle$ がそれぞれ 50 % の確率で観測される状態をとることになります。
このような状態は2量子ビットの量子もつれ状態 (Bell状態) と呼ばれていて、
この状態を作り出すことが、量子コンピュータにおける Hello World プログラムになります。
$|01\rangle$ や $|10\rangle$ といった状態を観測できる確率が 0 % なところも特徴となっています。
| $q_0$ | $q_1$ | H $\rightarrow$ CNOT |
|---|---|---|
| 0 | 0 | 00 |
| 1 | 0 | 11 |
Bell状態では例えば $|q_0\rangle$ を観測して $|1\rangle$ が観測できたとすると、その瞬間に $|q_1\rangle$ を観測していなくとも、$|11\rangle$ に確定します。つまり、片方のビットの状態の観測によって、もう片方のビット重ね合わせ状態も壊れるということです。
このことは、$|00\rangle$ or $|11\rangle$ という状態は、独立した二つの量子ビットの状態として分解できないということによるものです。
この節の話を簡単にまとめると
Hello Worldプログラム = 2量子ビットの量子もつれ状態 (Bell状態) を作成すること。
Bell 状態では片方の量子ビットを観測するとそのビットの状態にもう片方の量子ビットもなる。
シミュレーション結果
ここまでの話でようやくHello Worldプログラムを理解できたことになります。
では、実際にシミュレーターを用いて実験をしてみます。
使用したシミュレーターは IBM Quantum Experience です。
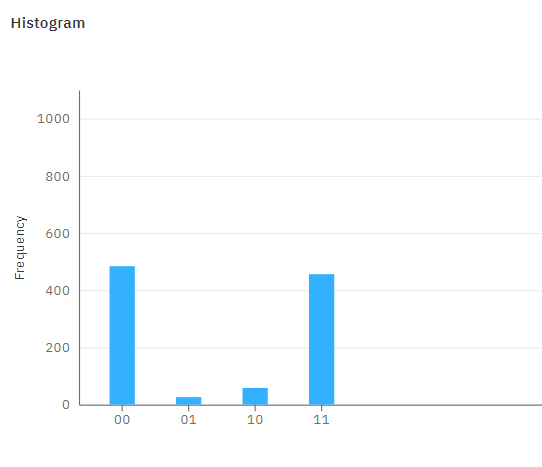
1024 回測定をした結果、次のようになりました。
縦軸が頻度で、横軸が観測された量子ビットの状態です。
上で $|00\rangle$ or $|11\rangle$ がそれぞれ 50 % の確率で観測される状態となるというお話をしましたが、
結果を見ると、確かに $|00\rangle$ と $|11\rangle$ が同じくらいの頻度で観測されていることが確かめられると思います。
また、$|01\rangle$ や $|10\rangle$ という状態は理論通り観測されていません。
実機の量子コンピュータによる計算結果
シミュレーションの結果、理論通りになっていることが確かめられました。
では、次に実機で実験を行ってみます。
シミュレーションを行った時と同じように、
1024 回測定を行った結果、次のようになりました。
測定結果を見てみると、$|00\rangle$ と $|11\rangle$ が同じくらいの頻度で測定されていることがわかりますが、$|01\rangle$ や $|10\rangle$ という状態も測定されていることがわかります。
原理的には、そのような状態は測定されないはずですが、実機ですとそのような状態が測定されてしまっています。
このことは、量子コンピューターの計算エラーによるものです。
このようなエラー自体は古典コンピュータにもありますが、古典コンピュータの場合良い精度のエラー訂正の仕組みがあります。
量子コンピューターには、古典コンピュータにあるような良い精度のエラー訂正の仕組みがまだないため、
結構な頻度でエラーが起きてしまうようです。
ともあれ実機ですとこのようなエラーが見られます。
まとめ
以上で、量子コンピューターのおける Hello World プログラムを理解することができたのではないかと思います。
まとめますと
1.量子コンピューターのおける Hello World プログラム = 2量子ビットの量子もつれ状態 (Bell状態) を作ること
2.Bell 状態では片方の量子ビットを観測するとそのビットの状態にもう片方の量子ビットもなる。
3.Bell状態では、$|00\rangle$ or $|11\rangle$ がそれぞれ 50 % の確率で観測される
4.実機だとエラーが出る
です。
なるべく定性的に説明をしましたが、線形代数などがわかるのであれば、
複数量子ビットともつれ状態 - Qiskit などを見るとより分かりやすいと思いますので、興味があればご覧になるとよいと思います。
参考文献
量子コンピュータが本当にわかる!
IBM Quantumで学ぶ量子コンピュータ
Quantum Native Dojo
複数量子ビットともつれ状態 - Qiskit