グロスマンモデル

覚えておきたい点をメモ
グロスマン(Grossman)により1972年に提唱された。健康資本投資に関するモデル。

基本

・$T$: ある時点
・$t$: 0からTまでのある時点
以下添字の$t$は時点tであることを示す。
・$Z_t$: 消費財の消費水準
・$X_t$: 消費財生産のための市場材の購入量
・$M_t$: $I_t$分の健康資本量を増加させるために必要な医療サービスの購入
・$H_t$: 健康資本の量
・$I_t$: 健康投資の量
・$\delta_t$: 減耗率

・時点0における健康資本
$$
H_0 = \bar{H_t}　\tag{1}
$$
・健康投資$I_t$を考慮した時点$t+1$における健康資本
$$
H_{t+1} = (1-\delta_t)H_t+I_t \tag{2}
$$

利用可能な時間の考慮

・$\Omega_t$: 所有する時間
・$TW_t$: 労働時間
・$TH_t$: 健康の損失により損失する活動時間
・$TM_t$: $I_t$分の健康資本量を増加させるために必要な自分の時間
・$TZ_t$: 消費財生産に投入する時間
・$w$: 賃金率
・$wTH_t$:　所得
・$R$: 割引現在価値額
・$A$: 初期資産保有額

$$
TH_t = TM_t+TZ_t+TW_t+TH_t \tag{3}
$$

$$
R = A+\sum_{t=0}^T{}\frac{wTW_t}{(1+r)^t} \tag{4}
$$

医療サービスM_tの価格をP_tとすると
$$
\sum_{t=0}^T\frac{(P_tM_t+X_t)}{(1+r)^t} \tag{5}
$$

収入=支出と仮定すると(4),(5)より

$$
A+\sum_{t=0}^T\frac{w\delta_t}{(1+r)^t} = \
\sum_{t=0}^T\frac{P_tM_t+X_t+w(TM_t+TZ_t+TH_t)}{(1+r)^t}　\tag{6}
$$

(6)を条件として、個人はZとHにおける効用を最大化する。

健康投資の最適条件に関して

・限界費用: 健康投資を限界的に増やした時に失う費用の変化分
・利子: 貯蓄に回しておけばえられたであろう利子

日常生活時間✖️(限界的賃金収入＋限界的効用増加) =
粗限界費用✖️(利子率-時間経過に要る限界費用の変化分+資本減耗率)

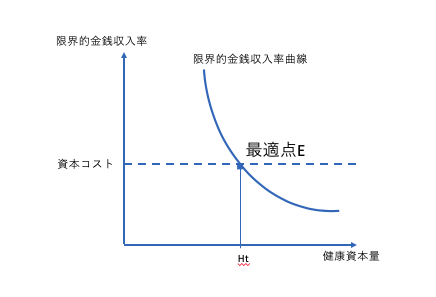
純粋投資モデル(効用関数が含まれない)は、
日常生活時間✖️限界的賃金収入/粗限界費用=
利子率-時間経過に要る限界費用の変化分+資本減耗率

*左辺: 限界的純金銭的収益率
*右辺: 資本コスト

課題点

■医療の不確実性の考慮がない
Arrow(1963年)が指摘

■死亡する時点で$H_{T}=0$とならない
=> 年齢を増すごとに資本減耗率が大きくなるようにする
$$\delta_{t+1} > \delta_t$$

■初期保有資産の水準(貧富の差)の考慮がない

参考文献

医療経済学講義　補訂版 橋本英樹・泉田信行