はじめに
「72の法則」と呼ばれるものを初めて知ったのはいつの日だったか。
貯金や借金がだいたい何年で2倍になるかを暗算で求めるための知恵らしい。
使い方は簡単で、72をx%で割った答えが年数になるというものだ。
year = 72÷x
というわけだ。
例えば、年利 3%で100万円を預けた時、24年で倍の200万円になるのだが、
72÷3=24 で、これまたぴったり24年と求まる。
証明はググるとすぐみつかる。
どうも72より69の方が誤差は少ないようだが、72の方が暗算しやすいということらしい。
(約数が多いからだろうか? 72=2x2x2x3x3)
また、大きめに出ることもメリットが多いように思う。
そんなことを思い出しながら、ふと僕はその精度が知りたくなった。
作成したコード
まずは、C言語でプログラムを書いてみた。
#include <stdio.h>
#include <math.h>
int main(void){
int year, expect, error;
double rate, deposit, error_ratio;
printf("rate[%%], year, expect, error, error ratio[%%]\n");
for(int i=1; i<=1000; i++){
rate = (double)i/1000.0;
for(year=0,deposit=1.0; deposit<2.0; year++){
deposit *= 1.0+rate;
}
expect = ceil(720.0/(double)i);
error = expect-year;
error_ratio = (double)error/year;
printf("%6.2lf, %8d, %8d, %8d, %6.2lf\n",
rate*100.0, year, expect, error, error_ratio*100.0);
}
return 0;
}
72を利息で割ると余りが出るが、利息が年に一回とすると、結果は整数である必要がある。そこで結果は切り上げとした。
出力はカンマ区切り文としてEXCELに張り付けやすいようにした。
printfで「%」を表示するには「%%」と書くというのを今回学んだ。
実行結果の一部
rate[%], year, expect, error, error ratio[%]
0.10, 694, 720, 26, 3.75
0.20, 347, 360, 13, 3.75
0.30, 232, 240, 8, 3.45
0.40, 174, 180, 6, 3.45
0.50, 139, 144, 5, 3.60
...
rate[%]...利率
year...2倍になる年数
expect...72の法則で求まった年数
error...誤差年数
error ratio[%]...誤差率
doubleに関する注意点
ループ変数は整数型にした。これは変化量を実数にすると誤差の蓄積が思わぬ結果をもたらす懸念があるためだ。例えば、
for(rate=0.001; rate<=1.0; rate+=0.001){
のように書くと、rateが1.0の時にループが実行されなかったりする。
また、72の法則を計算するときに
expect = ceil(72.0/(rate*100.0));
としたら、rate=0.009の時にexpectが80ではなく81になってしまった。
とかくdoubleは、整数との比較や整数化関数で予期せぬ結果をもたらす。
精度の確認
計算結果
さて、この結果を使ってグラフを書いてみよう。
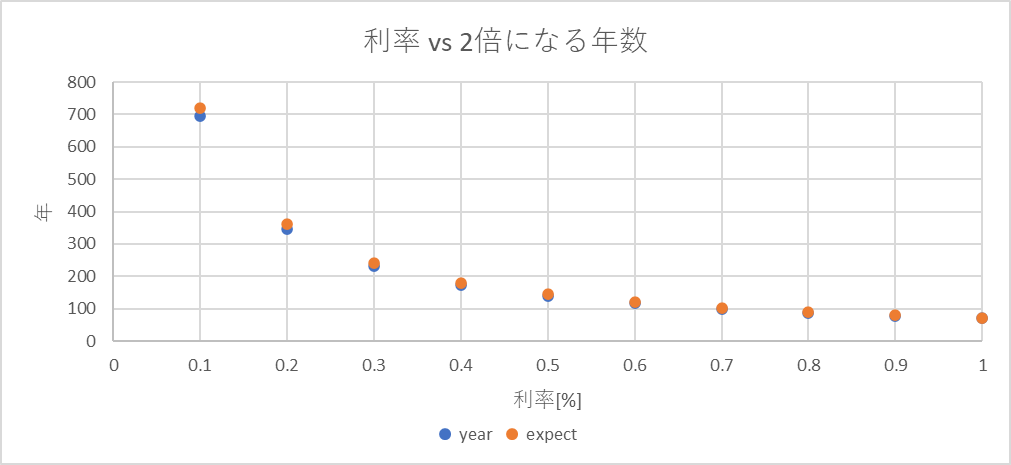
まず、0.1%~1.0%。
少しずれがみられる。
0.1%の貯金が2倍になるのに、ほぼ700年かかる。世知辛い。
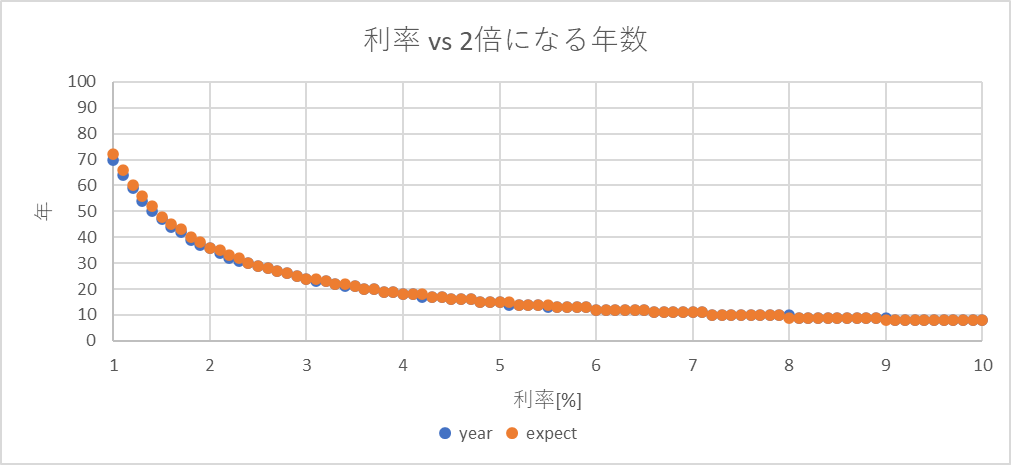
次に、1.0%~10.0%。
ほぼずれは見られない。
4%の借金は18年で2倍になる。つらい。
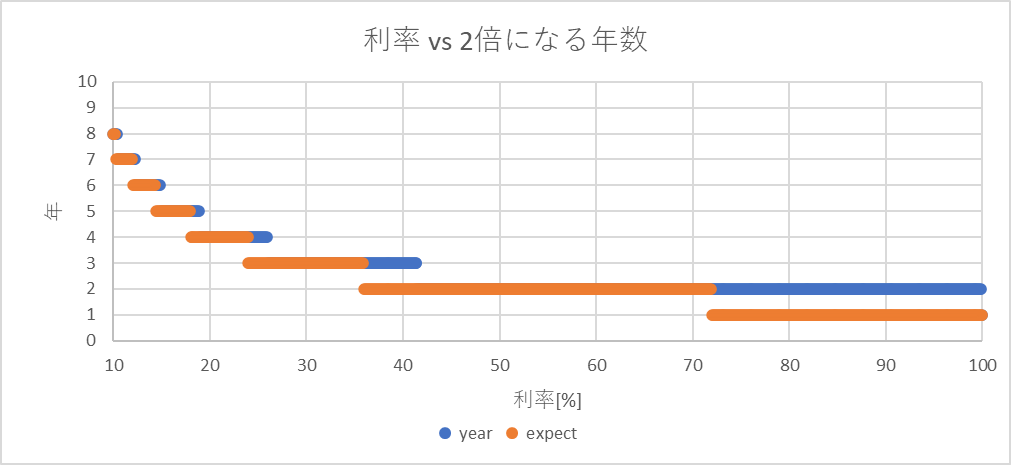
次に、10.0%~100.0%。
1年以下のずれにとどまるのが見て取れる。
年利でこの率はあまり見かけない。
誤差の確認
ずれを調べるために、誤差のグラフを書いてみよう。
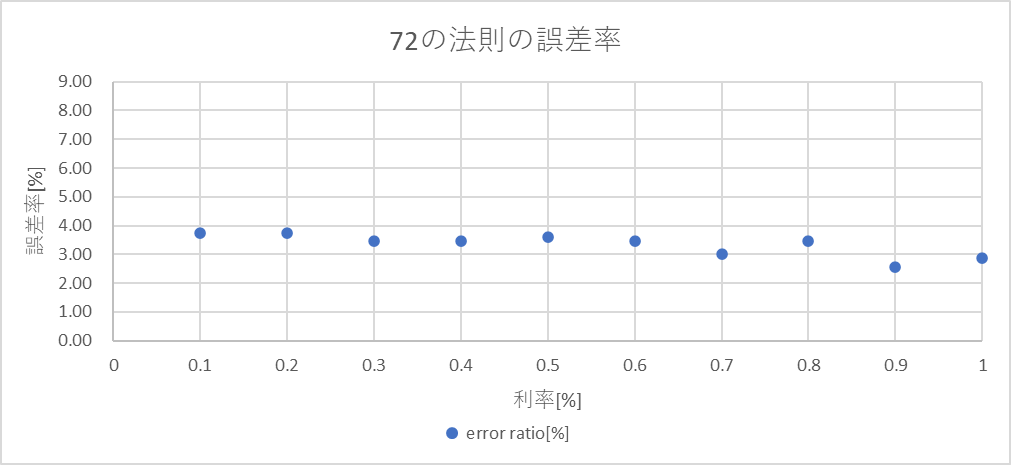
まず、0.1%~1.0%。
絶対値が大きいため、誤差が大きく見える。
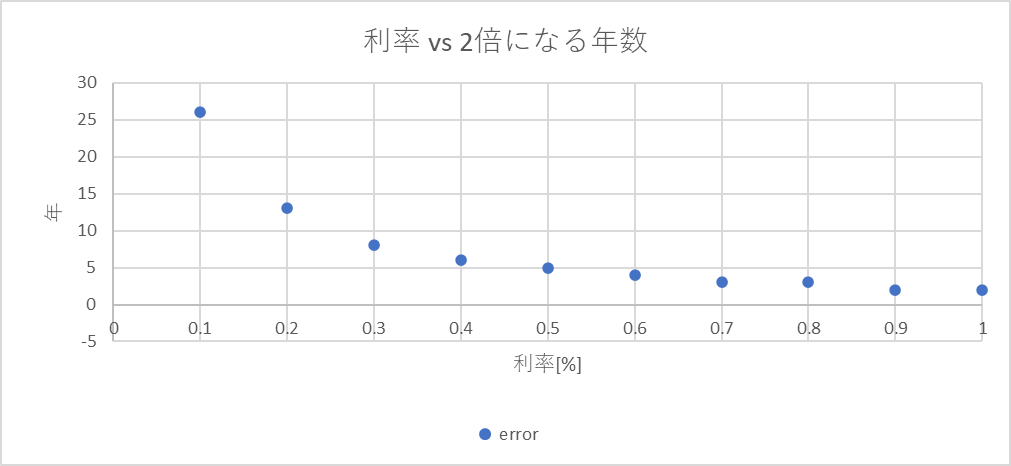
比率をみてみると、4%弱に収まっていることがわかる。
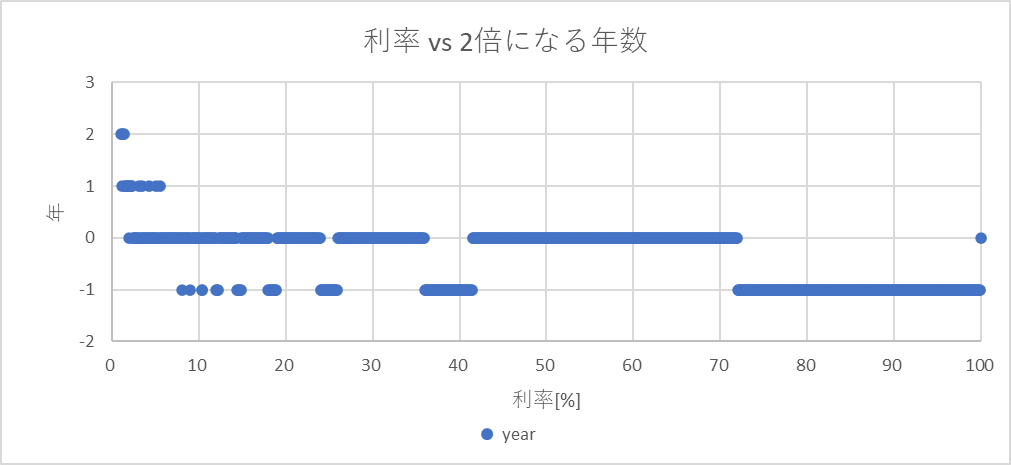
次に、1.0%~100.0%。
ほぼ±1年の誤差に収まっていることがわかる。
また、8%あたりから72の法則の方が(繰り上げで計算しているにも関わらず)マイナスになることがあることには注意が必要だろう。
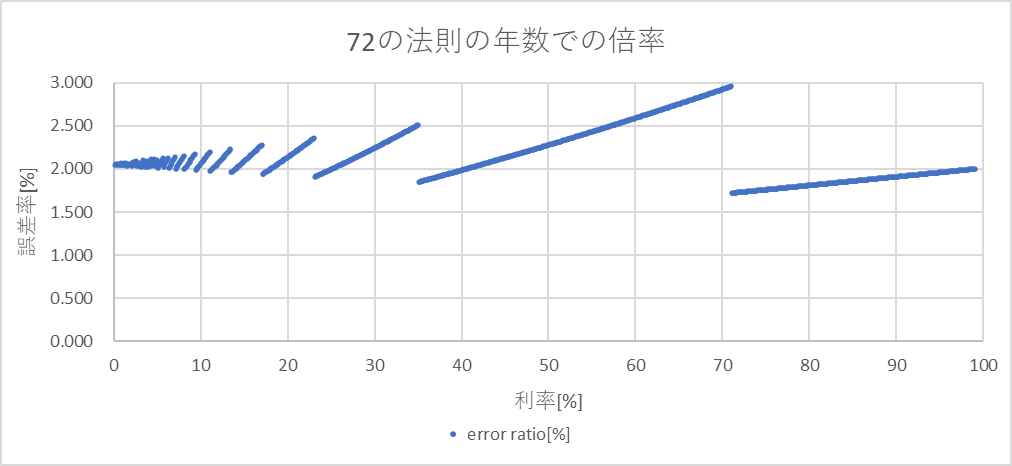
このことは、72の法則で計算した年数で何倍になるかをみるとわかりやすい。
72の法則で計算した結果は、大きめに出やすいが必ずしもそうではないことがわかる。
最後に比率をみてみると、整数化の影響でとても誤差が大きく見える。
1%以上で誤差率を議論するのは不適切だろう。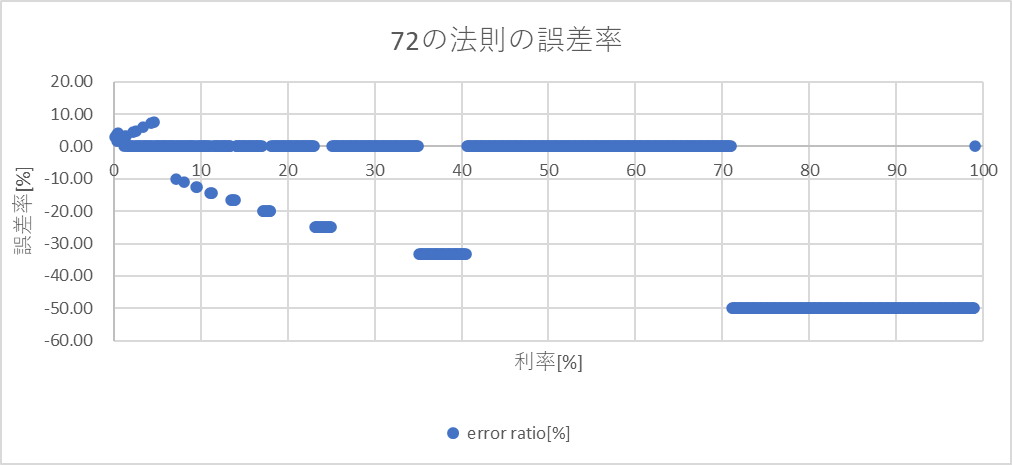
おわりに
72の法則は大きめに出ると思っていたら案外少なめに出る場合があることが分かった。ただそれは高々マイナス1年程度であり、マイナスになるのは8%以上であることが確認できた。
また、久しぶりにC言語でdoubleを使ってみたが、やはり整数との変換や比較には注意が必要であることを痛感した。EXCELでも同様の経験があり、10進演算ライブラリがあれば使ってみたい。
免責事項
本記事の正確性については努力しておりますが、当方は利用者が当記事の情報を用いて行う一切の行為について何ら責任を負うものではありません。本記事の情報の利用、内容によって、利用者にいかなる損害、被害が生じても、著者は一切の責任を負いません。ご自身の責任においてご利用いただきますようお願いいたします。
商標について
本記事に掲載されている商品またはサービスなどの名称は、各社の商標または登録商標です。