はじめに
デジタル信号処理をプログラミングしたりソフトウェア無線機(SDR : Software Defined Radio)を作る際に、複素数同士の掛け算が必要になることがあります。古典的なマイコンで掛け算を行うと実行時間がかかるし、FPGAなら回路リソースや消費電力が気になります。FFTや複素バンドパスフィルタになるとひたすら複素数の掛け算をすることになるし、もっとうまい方法はないのかなって思ったことはありませんか?
もしかしたらこの記事が役に立つかもしれません。
複素数の積を基本式で求める
2つの複素数 $X=a+ib,\quad XY=c+id$ の積 $Z=e+if$ を基本式で計算すると
$Z=X\times Y$
$=(a+ib)\times (c+id)$
$=(a\times c-b\times d)+i(a\times d+b\times c)$
となりますので、$z$ の実部 $e$ 及び虚部 $f$ は実数値同士の計算、
$e=a\times c-b\times d$
$f=a\times d+b\times c$
で求めることができます。
図で書くとこうなります。
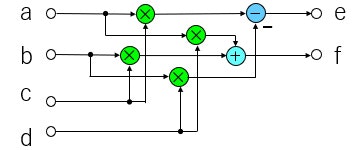
このように、基本式通りの計算では4回の掛け算と1回の足し算と1回の引き算が必要になります。
掛け算は足し算と比べて(ハードウェア乗算器を持たない)マイコンでは実行時間がかかったり、FPGAなどのハードウェアでは回路規模が増大したりします。そこで、掛け算回数を減らす方法について紹介したいと思います。
乗算回数を減らしてみる
もう一度2つの複素数 $X=a+ib,\quad Y=c+id$ の積 $Z=e+if$ を計算してみましょう。
今度は実部と虚部で同じ掛け算が現れるように工夫をしてみます。
なお、以下の数式では、数式を追いやすいように "$\times$" は省略します。
$Z=XY$
$=(a+ib)(c+id)$
$=(ac-bd)+i(ad+bc)$
$=(ac+ad-ad-bd)+i(ad+bd-bd+bc)$
$=(a(c+d)-d(a+b))+i(b(c-d)+d(a+b))$
よって、$z$ の実部 $e$ 及び虚部 $f$ は実数値同士の計算、
$e=a(c+d)-d(a+b)$
$f=b(c-d)+d(a+b)$
で求めることができます。
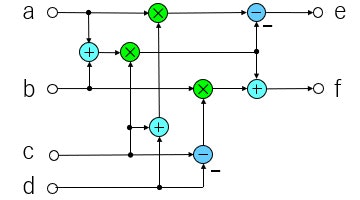
ここで右辺の $d(a+b)$ が重複しているので、3回の掛け算で複素数の積を求められることになります。
図で書くとこうなります。
定数や変更頻度の少ない値で威力を発揮する
さて、確かに掛け算は3回に減りました。でも、代わりに足し算や引き算が3回も増えて計5回になってしまいました。
なんだか、あまり得した気分になりませんね。でも実は、使い方を考えるとそうでもありません。
実際に複素乗算が必要になるシチュエーションでは、乗算の片側が定数であったり時々しか値を変えないことがよくあります。例えば、複素バンドパスフィルタであれば特性は設計時に決まりますのでフィルタ係数は定数になります。$Y$ 側を定数とすると、$c-d$と$c+d$は事前に計算しておくことができますので、$Z$を1個求めるために必要な計算量は
基本式)4回の掛け算と1回の足し算と1回の引き算
変形後)3回の掛け算と2回の足し算と1回の引き算
となり、掛け算を足し算に置き換えたくらいの効果が期待できることがわかります。
また、時々しか値を変えない値を $Y$ 側にすると $c-d$と $c+d$ の計算は時々ですのでやはりお得に見えてきます。
よってこの変形は、処理速度向上や消費電流の削減に貢献できそうです。
バリエーションを並べてみる
この変形には共通項の作り方で色々なバリエーションが考えられます。
$ \begin{eqnarray}
e=ac-bd=
\begin{cases}
ac+ad-ad-bd&=
\begin{cases}
a(c+d)-d(a+b)\
a(c-d)+d(a-b)
\end{cases}\
ac+bc-bc-bd&=
\begin{cases}
-b(c+d)+c(a+b)\
b(c-d)+c(a-b)
\end{cases}
\end{cases}
\end{eqnarray} $
$ \begin{eqnarray}
f=ad+bc=
\begin{cases}
ad+bd-bd+bc&=
\begin{cases}
b(c-d)+d(a+b)\
b(c+d)+d(a-b)
\end{cases}\
ad+ac-ac-bc&=
\begin{cases}
a(c+d)-c(a+b)\
-a(c-d)+c(a-b)
\end{cases}
\end{cases}
\end{eqnarray} $
ここに示した $e$ や $f$ を導出する数式の右辺から共通項を持つものを組み合わせると、掛け算を3回、加減算を5回にする式のペアができます。残念ながらか加減算の見た目の回数は減りませんが、お使いのシチュエーションに適したペアがあるかもしれませんね。
複素共役と乗算してみる
複素共役との掛け算も同様に計算できます。
$Z=X \bar{Y}$
$=(a+ib)(c-id)$
$=(ac+bd)+i(bc-ad)$
$=(ac+ad-ad+bd)+i(bc+bd-bd-ad)$
$=(a(c-d)+d(a+b))+i(b(c+d)-d(a+b))$
よって、$z$ の実部 $e$ 及び虚部 $f$ は実数値同士の計算、
$e=a(c-d)+d(a+b)$
$f=b(c+d)-d(a+b)$
で求めることができます。
図で書くとこうなります。
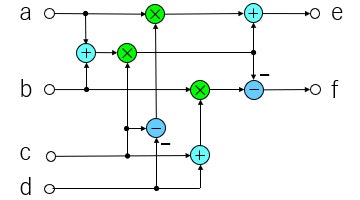
この場合も乗算を3回、加減算を5回で計算できます。複素共役を作るための符号反転の演算は不要であることがわかります。
他のバリエーションも、先の式の $d$ を$-d$ に置き換えることで求めることができます。
アフィン変換にも適用してみる (2020/12/9追記)
画像処理で用いる原点を中心に角度 $θ$ だけ回転するアフィン変換も複素数同士の掛け算と同じ構造を持っています。
そこで、同様に変形してみましょう。
$ \begin{eqnarray}
\left( \begin{array}{c}
u \\ v
\end{array}\right)
=& \left( \begin{array}{cc}
cosθ & -sinθ \
sinθ & cosθ
\end{array} \right)
\left( \begin{array}{cc}
x\
y
\end{array} \right) \
=& \left( \begin{array}{cc}
x,cosθ-y,sinθ \
x,sinθ+y,cosθ
\end{array} \right) \
=& \left( \begin{array}{cc}
x,cosθ+y,cosθ-y,cosθ-y,sinθ \
x,sinθ+x,cosθ-x,cosθ+y,cosθ
\end{array} \right) \
=& \left( \begin{array}{cc}
(x+y),cosθ-y,(cosθ+sinθ) \
(x+y),cosθ-x,(cosθ-sinθ)
\end{array} \right)
\end{eqnarray} $
ここで右辺の $(x+y),cosθ$ が重複しているので、3回の掛け算で回転するアフィン変換を求められることがわかります。
代わりに足し算や引き算が3回増えて計5回になってしまいますが、アフィン変換では同じ角度 $θ$ での回転を繰り返しますので、$cosθ+sinθ$と$cosθ-sinθ$を毎回計算する必要はありません。最初に1回計算するだけで済みます。
よって毎回計算する加減算は3回ということになります。
まとめると毎回必要な計算量は
基本式)4回の掛け算と2回の加減算
変形後)3回の掛け算と3回の加減算
となり、掛け算1回を加減算1回に置き換えたくらいの効果が期待できることがわかります。
おわりに
プログラミング言語を限定せずに複素乗算の実数乗算回数を減らす方法について書いてみました。
定数や変更頻度の少ない値との複素乗算では、掛け算1回を足し算1回に置き換えたくらいの効果が期待できます。
貧弱な環境でデジタルフィルタのような複素乗算を大量に実行する場合にはこの違いが馬鹿にできないと思います。
このテクニックは画像回転で用いられるアフィン変換にも有効です。
Advent Calendar企画に合わせて初めてQiitaに記事を書くにあたり、練習がてら記事にしてみました。
お役に立てば幸いです。