はじめに
ゲームを作るとき、N個の自然数で重複しない乱数列を作りたい時がありますよね。
昔BASICで書いたものを思い出して、C言語で書いてみました。
高速でメモリ使用量も少ないシンプルなプログラムかと思います。
サンプルコード
こんなコードで実現できます。
# include <stdlib.h>
# define swap(type,a,b) {type __tmp=a;a=b;b=__tmp;}
// 1~numまでの重複しない乱数を作る関数
void getrands(int *numbers, int num){
int i, n;
for( i=1; i<=num; i++ ){
numbers[i] = i;
}
for( i=num; i>1; i-- ){
n = rand() % i + 1;
swap(int, numbers[i], numbers[n]);
}
}
見たままですが、動作を説明すると
(1) 1~num の値を配列にセットする。
(2) i=num とする。
(3) 配列の i 番目の要素と i 以下の乱数番目の要素の中身を入れ替える。
(4) i を 1 つ小さくして、i が 1 より大きかったら (3)に戻る。
(5) i が 1 になったら終了。
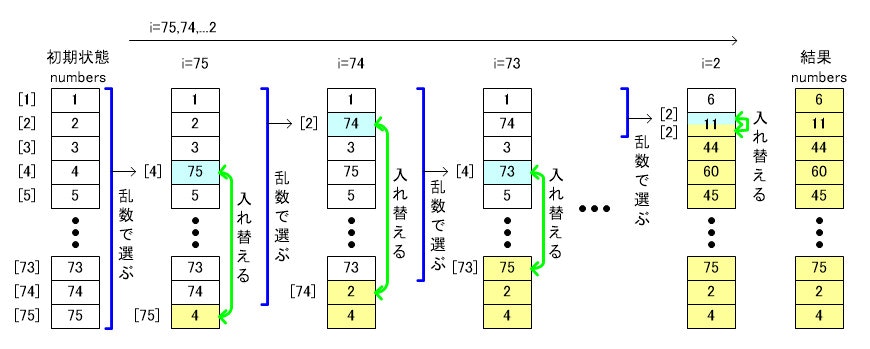
例として num=75 の時に乱数が決まっていく様子を図1に示します。
numbers[75] から順に値を決めていき、最後に numbers[2] の値が決まれば終わりです。
i=2 に例示したように乱数 n と i が一致する場合もあります。
この時本来 swap は不要ですが、条件分岐は遅いことが多いので常に swap 動作するプログラムとしています。
呼び出しプログラムの例
# include <stdio.h>
# include <time.h>
# define RNDMAX 75
void getrands(int *numbers, int num);
int main(void){
int i, numbers[RNDMAX+1];
srand((unsigned int)time(NULL));
getrands(numbers, RNDMAX);
for( i=1; i<=RNDMAX; i++ ){
printf("%d%s", numbers[i], i==RNDMAX ? "\n" : ", ");
}
return 0;
}
実行結果の例
6, 11, 44, 60, 45, 20, 5, 69, 41, 15, 8, 63, 10, 9, 42, 19, 64, 39, 71, 23, 7, 73, 21, 35, 49, 50, 30, 74, 36, 27, 28, 62, 43, 38, 40, 70, 17, 24, 59, 47, 68, 33, 67, 13, 53, 55, 61, 37, 26, 1, 18, 25, 48, 54, 65, 29, 16, 3, 51, 31, 66, 22, 57, 12, 72, 14, 56, 32, 58, 52, 34, 46, 75, 2, 4
余談
学生時代にビンゴゲームを作る際に考えたアルゴリズムが元になっています。
ググってみると Wikipedia に同じアルゴリズムが紹介されていました。「リチャード・ダステンフェルド」さんが1964年に紹介されたアルゴリズムと同じです。自分のは車輪の再発明ですね。
ところが、Fisher–Yates shuffle が先にあって、ダステンフェルドさんのはその改良とみなされるようです。シビアですね。特許なら別の特許として通りそうです。
こういう情報がググれるようになってからは自分でいちいち考えなくて済むようになりましたが、車輪の再発明と恐れずに自分で考えてから答え合わせのつもりでググるのも楽しいものですね。
おわりに
頻繁に車輪の再発明される便利なアルゴリズムのご紹介でした。
リーチしやすさの向上に、また何かのヒントに一役買うことができたら幸いです。
免責事項
本記事の正確性については努力しておりますが、当方は利用者が当記事の情報を用いて行う一切の行為について何ら責任を負うものではありません。本記事の情報の利用、内容によって、利用者にいかなる損害、被害が生じても、著者は一切の責任を負いません。ご自身の責任においてご利用いただきますようお願いいたします。
商標について
本記事に掲載されている商品またはサービスなどの名称は、各社の商標または登録商標です。