超初心者が学ぶランダムフォレスト・分類回帰樹木 ⑤ ランダムフォレスト編の続きみたいな感じです
こちらでランダムフォレストについては説明してあります。
PDP (Partial Dependence Plot)
直訳すると「部分従属度」です。ランダムフォレストでは通常複数個の説明変数を用いてモデルを作成しますが、ある1つの説明変数と目的変数の関係を見たいとします。その時、残りの変数の動きを周辺化(無視)して1変数のみに依存した動きを観測できるのがPDPです。
さらに詳しく
着目する説明変数を$x_s$、その他の説明変数を$x_c$と定義します。
$x_s$のPDPは
$\hat{f}_{x_s}(x_s)=Ex_c[\hat{f}(x_s,x_c)]=\int \hat{f}(x_s,x_c)dP(x_c)$
と定義されます。ここで$dP(x_c)$は$x_c$の周辺確率密度です。$x_c$で積分することで、今回の観測対象外である$x_c$は消去してしまおうという方法です。
さて、ランダムフォレストは通常数百本の決定木をアンサンブル学習させることでモデルが生成されます。この決定木の数を$n$とすると、関数$\hat{f}_{x_s}$も$n$本できるので、これらを平均化したものがPDPになります。式で示すと
$\bar{\hat{f}_{x_s}}(x_s)=\dfrac{1}{N}\sum_{i=1}^{N}\hat{f}(x_s,x_c^{(i)})$
で推定されます。
変数重要度:どの変数に着目する?
ランダムフォレストで1変数の動きを見られるのはわかった!さて、じゃあどの変数を見たら良いのだろう・・・
という時に参考になるのが変数重要度です。
変数重要度を算出するのは様々な基準があり、ランダムフォレストは決定木を用いているのでジニ係数の減少量が用いられたりもします。一番単純な方法はPermutationと呼ばれる、どの変数を抜いた時に予測誤差が大きくなるかというシンプルなものです。「変数$x_s$を抜いたら予測誤差がめっちゃ大きくなった!これは重要な変数だ!」といった感じです。
調べ方は非常に簡単です。ボストン住宅価格のデータセットを用いてRで見てみましょう
> rf <- randomForest(medv~.,data=Boston)
> rf$importance
IncNodePurity
crim 2447.0552
zn 268.1384
indus 2544.3938
chas 251.8683
nox 2766.3590
rm 12170.1843
age 1181.2138
dis 2511.5008
rad 329.8089
tax 1304.3789
ptratio 2843.8737
black 800.1817
lstat 12416.2608
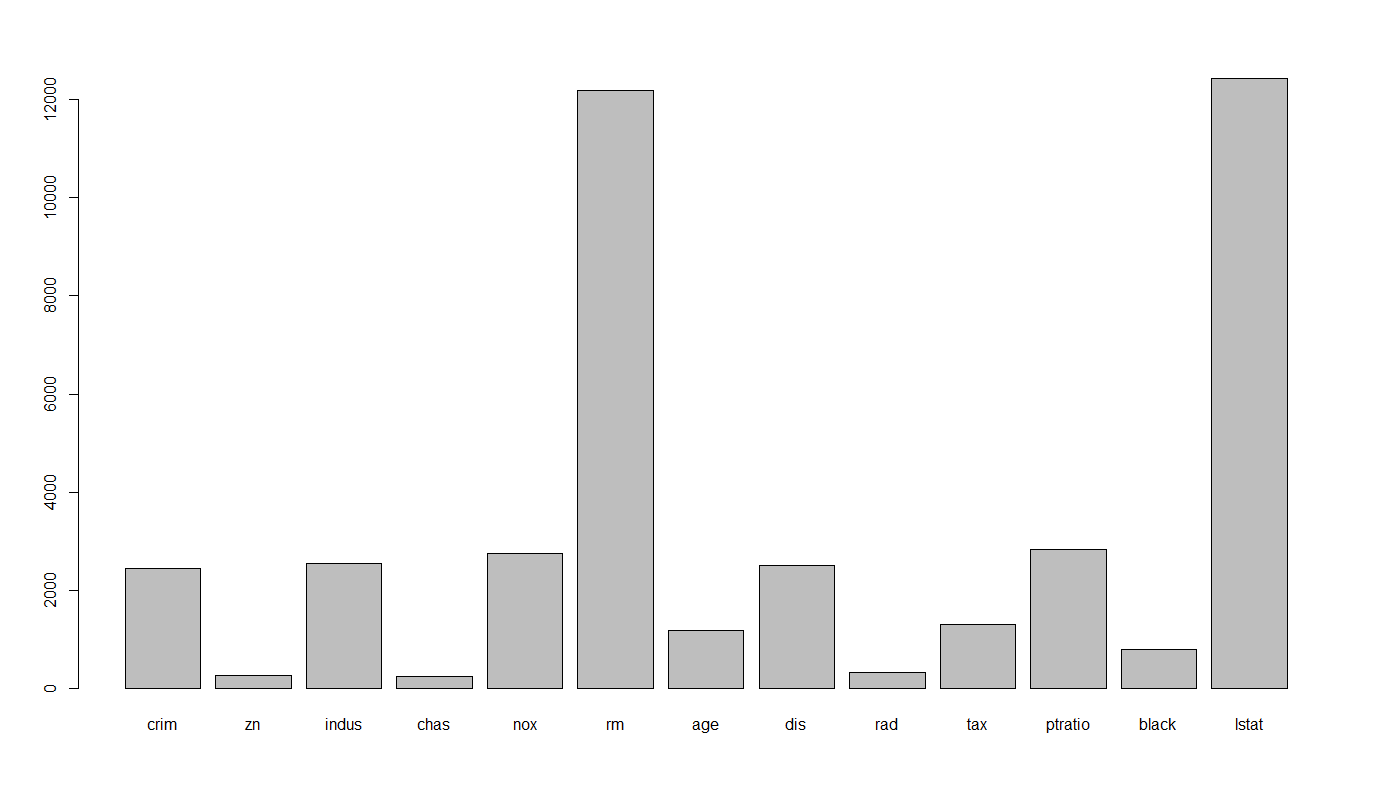
lstat(低所得人口の割合)とrm(1戸当たりの「平均部屋数」)の重要度が大きいですね。可視化もしてみましょう。
rf$importance[,1] %>% barplot()
こうやってみるとだんとつなのがわかりますね。それではrmとlstatについてPDPを見てみましょう
PDPの可視化
PDPを描き、それをloessで局所平滑化してみます。
library(pdp)
library(ggplot2)
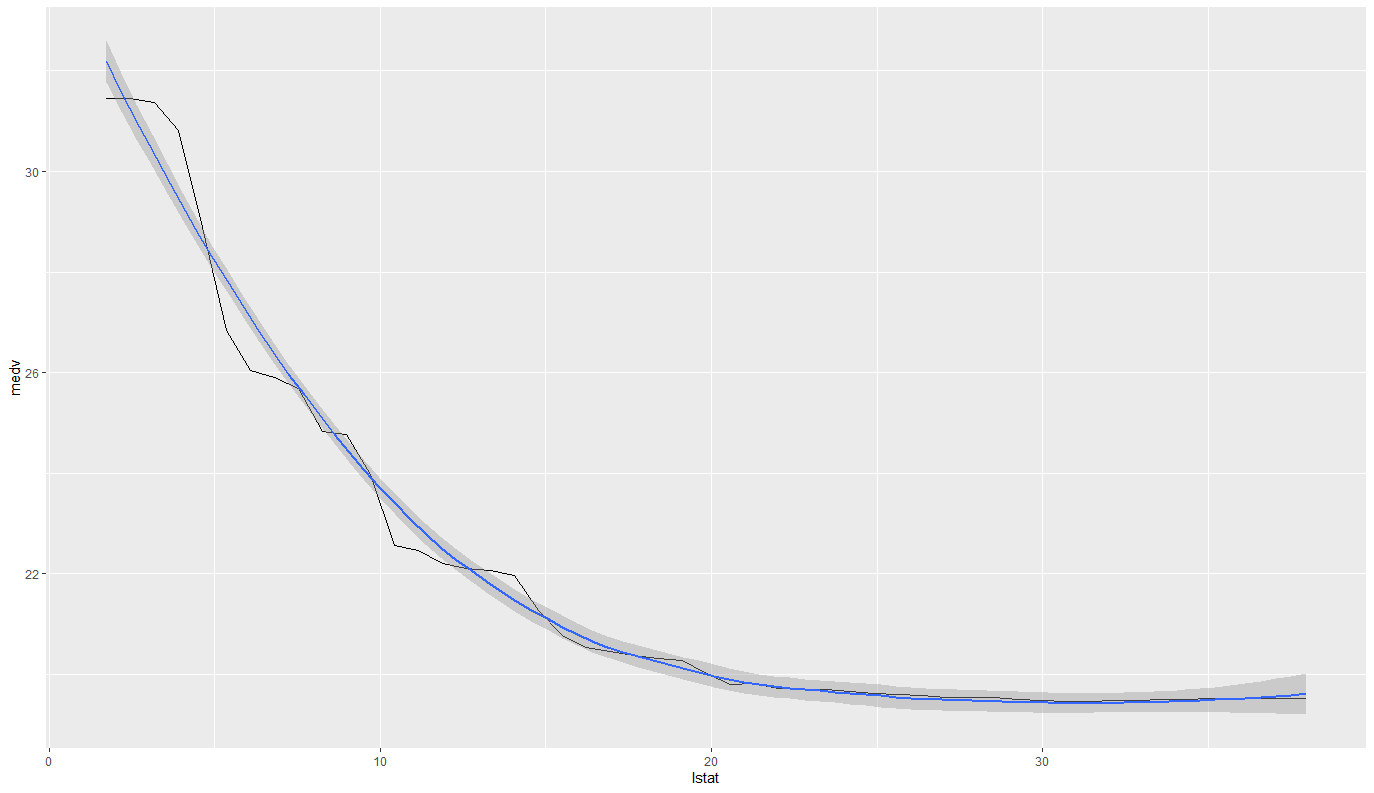
rf %>% partial(pred.var="lstat") %>% autoplot(ylab="medv") + geom_smooth(method = "loess")
lstatが大きくなるとmedvも小さくなります。低所得人口の割合は25%超えたあたりから下げ止まりしている感じがありますね。
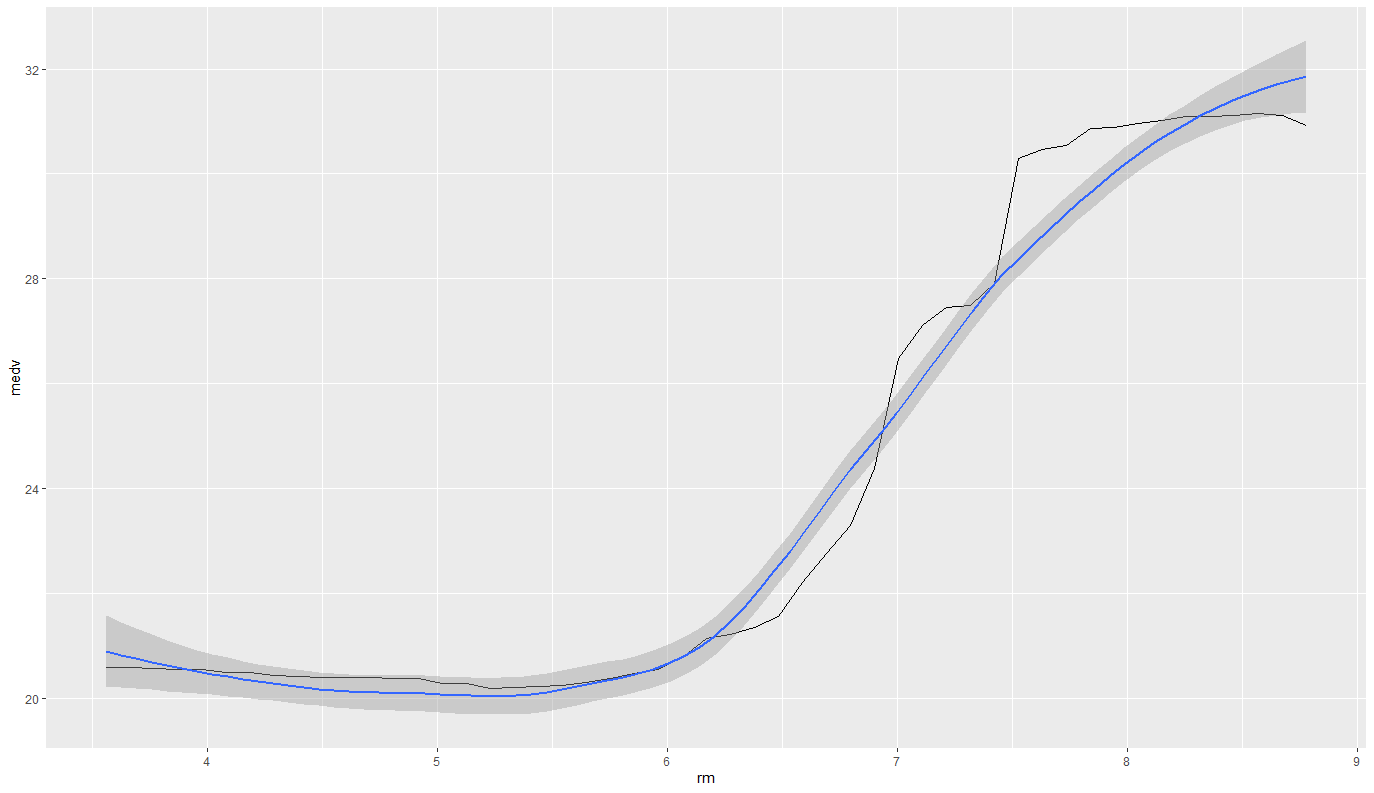
rf %>% partial(pred.var="lstat") %>% autoplot(ylab="medv") + geom_smooth(method = "loess")
部屋数は6までは大きな変化なし、7以上で爆上がりしています。一番お買い得なのは6部屋なのかな?とか想像が膨らみますね。
2つも重要な変数があるんだからまとめて見たいんだけど
そんなご要望にもお応えできます。PDPは2つの説明変数を3次元で可視化することも可能です。
解釈をより深くするために説明変数同士の関係も見ておきましょう。
## 3次元プロット
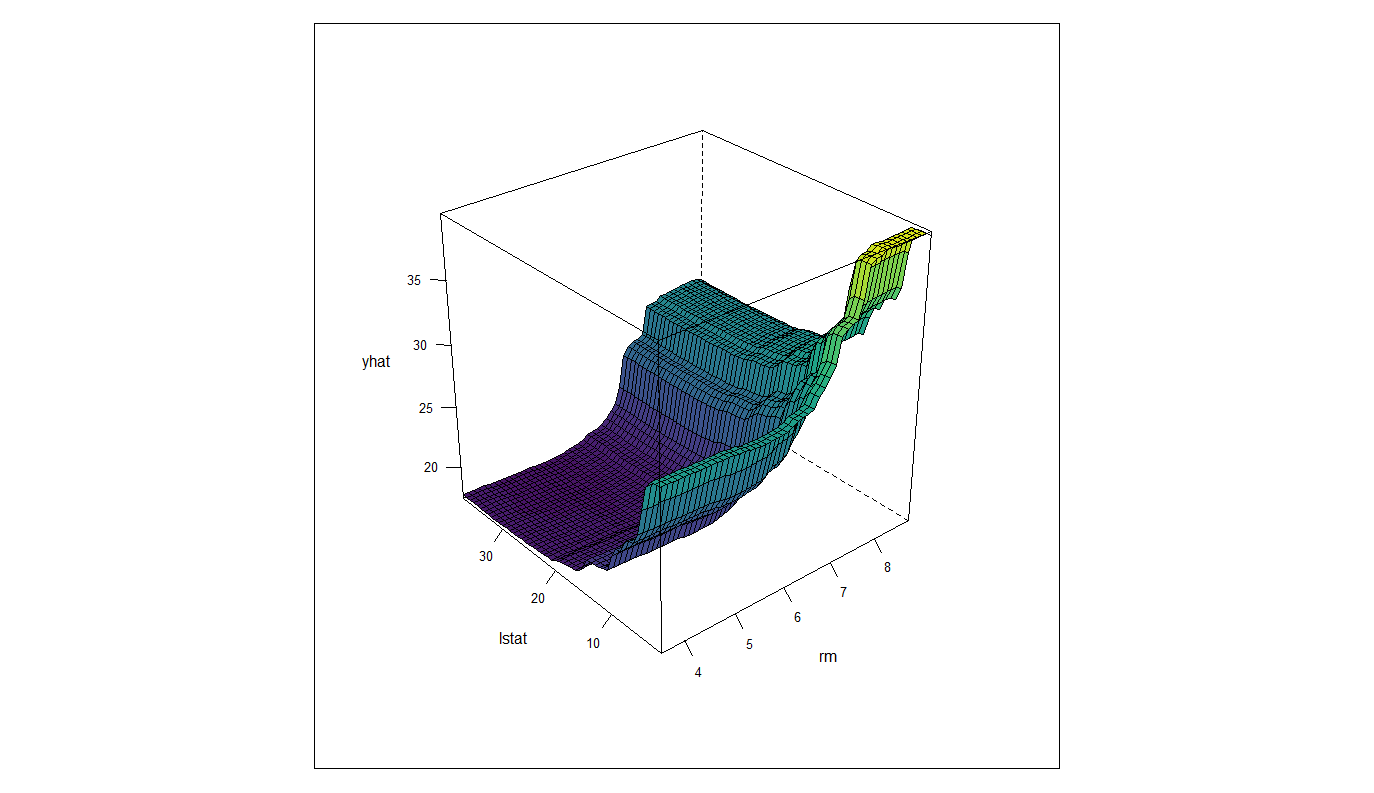
rf %>% partial(pred.var=c("rm","lstat"),parallel = T) %>%
plotPartial(levelplot = F,colorkey=F,plot.pdp = F,drape=T,scale=list(arrows=F),plot.margin= unit(c(0, 0, 0, 0), "lines"))
## 説明変数同士のプロット
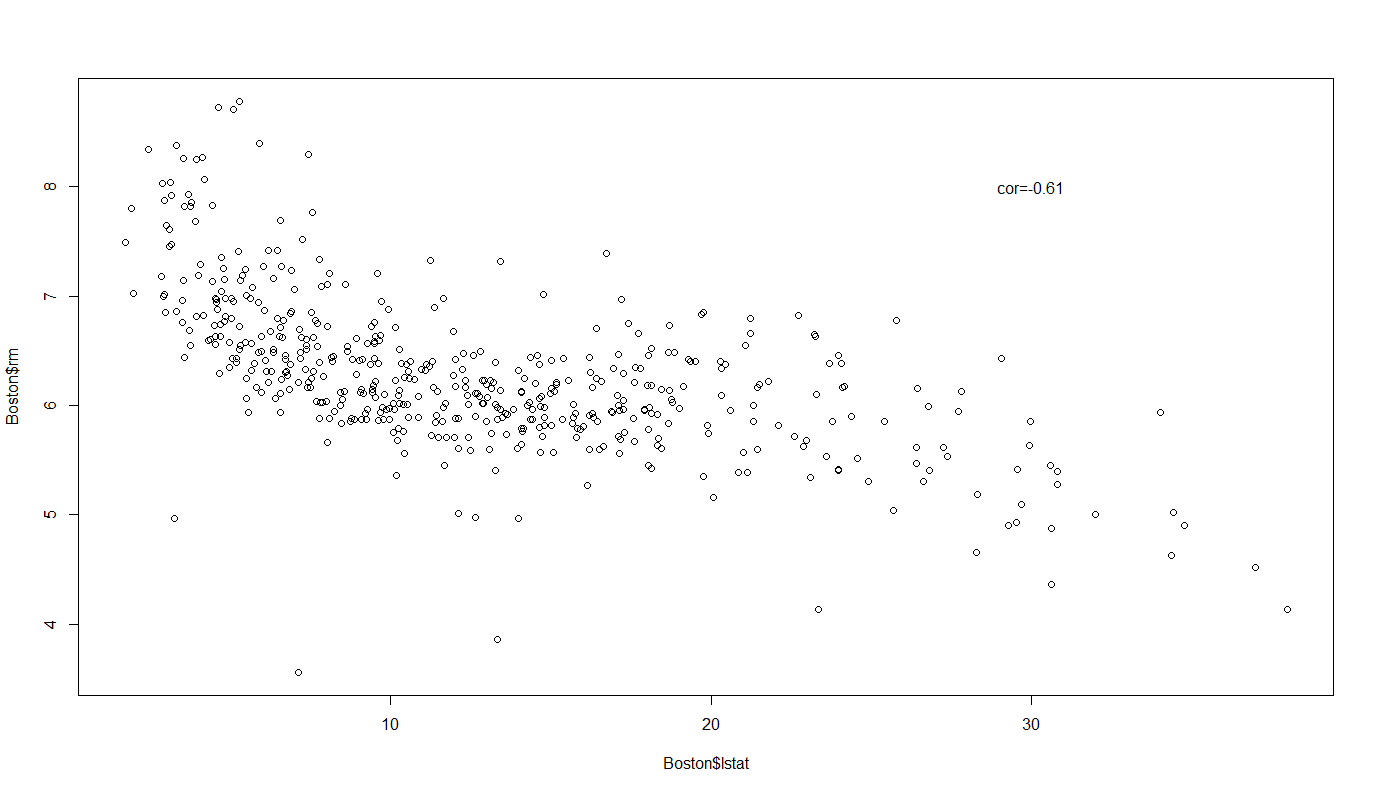
plot(Boston$lstat,Boston$rm)
## 説明変数同士の相関
> cor(Boston$lstat,Boston$rm)
[1] -0.6138083
そもそもlstatが10を超えたあたりで部屋数8以上が無く、lstat30以上になると部屋数7も見当たりません。なので3次元プロットでのlstat<30かつ部屋数>=7の部分は外挿域と考えた方がよさそう。
そうやって改めて考えてみると部屋数が6までなら、価格はlstatに逆行する形で変動しています。相関係数が約-0.61ということからも、妥当だと考えられそうですね。
コスパとしては6部屋でlstat=15くらいのとこが一番良さそう。
PDPは奥深い
今回は可視化だけでしたが、PDPから各プロットの値や平滑化曲線に対応した値も見ることができます。より正確な数値を知りたい場合はどんどん情報を得ることができます。日本語だとあまり文献はないかもしれませんが、英語のレファレンスなんかはたくさんあるのでググって探してみるのがおすすめです。
参考図書・url
Rで学ぶデータサイエンス9
https://dropout009.hatenablog.com/entry/2019/01/07/124214
https://christophm.github.io/interpretable-ml-book/pdp.html
https://www.rdocumentation.org/packages/pdp/versions/0.7.0/topics/plotPartial