#はじめに
2020年12月末より発生した、JEPX（日本卸電力取引所）のスポット市場価格の高騰について、対策として需給曲線（入札カーブ）の公開が始まりました。
一方で画像データということもあり、分析を進めていくために（まずはざっくりと）Pythonを活用して数値データに変換してみました。
#スポット市場とは？
まずはスポット市場ですが、以下のように書かれています。
一日前市場（スポット市場）
翌日に受渡する電気の取引を行う市場です。一日を30分単位に区切った48商品について取引を行います。約定方式はブラインド・シングルプライスオークションです。ブラインド・シングルプライスオークションとは…
入札価格によらず約定価格で取引されます。例えば、¥10/kWhで売りの入札を出していても、約定価格が¥15/kWhであれば、¥15/kWhで売られることになります。ブラインドとは、入札時に他の参加者の入札状況が見えないことを指します。
スマートメーターなんかだと30分ごとに電気の使用量が把握できたりしますが、市場の単位と揃えているんでしょうね。
市場参加者は買いもしくは売りの入札金額と入札量を提示します。買い入札の入札金額を降順に並べたものと、売り入札の入札量を昇順に並べたものの交点が約定価格となります。
これが後段で取り上げる需給曲線（入札カーブ）です。
買い入札量と売り入札量のデータはこちらから取得可能です。（取引結果）
#スポット市場価格とは？
続いてスポット市場価格ですが、システムプライスとエリアプライスがあります。この記事ではシステムプライスを取り上げています。
システムプライスとは…
スポット取引の約定計算で得られた全国大の売り入札曲線と買い入札曲線の交点の価格です。
スポット市場価格のデータはこちらから取得可能です。（取引結果）
時系列推移を見てみると、2021年1月に200円/kWhを超える高騰が発生している様子がわかります。ご家庭の電気料金プランを市場連動型にしていて、電気代が普段の数倍に膨れ上がった、なんて話をたまに聞きます。
今回の高騰の一つの対策として、2020年12月以降の需給曲線（入札カーブ）の画像データが公開されるようになりました。
画像データはこちらから取得可能です。（スポット市場における入札カーブ）
###2021年3月1日7:30~8:00の需給曲線（入札カーブ）例
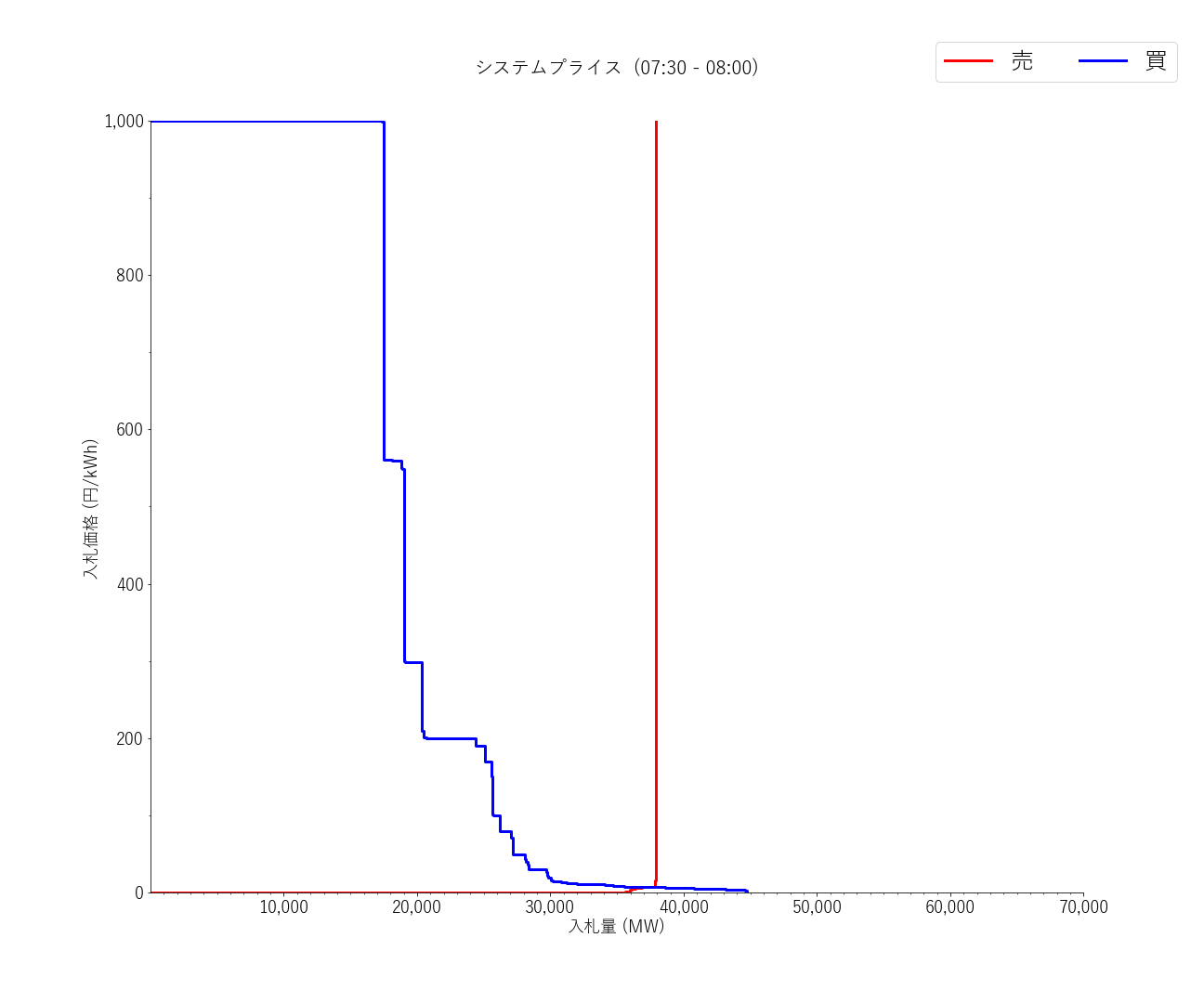青線が買い入札の入札金額を降順に並べたもの、赤線が売り入札の入札量を昇順に並べたものです。交点が(約定量,約定価格)となります。
注意点として、数値データは与えられておらず、画像データのみです。定量的な分析を進めていくため、数値データへの変換を行います。
#数値データへの変換
先程の2021年3月1日7:30~8:00の需給曲線（入札カーブ）を例に進めていきます。
#ライブラリのインポート
import pandas as pd
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
img = Image.open(filepath).convert('P') #画像の読み込み。filepathは画像のパス
np_img = np.array(img)#数値データへ変換
np_img = np.flipud(np_img)
print(np_img.shape)
#(1080, 1296)
画像をRGBではなく256色のパレットモードで読み込んでいますが、使われている色が少ないのと取扱いが簡単なので、一先ずこちらで進めていきます。（ざっくりポイント①）
数値データとしては、1080×1296の行列になっています。値は色の番号が振られています。
plt.figure(figsize=(6, 5))
for no in [1,2]:
np_temp = np.where(np_img==no)
plt.scatter(np_temp[1],np_temp[0],s=1)
plt.show()
色番号1,2がそれぞれ買い入札量、売り入札量のようです。
右上の凡例を取り除いておきます。
またピクセル単位になっているので、グラフの特性を基に数値データに直します。
プロットエリアの座標やメモリの最小最大値など、画像の形式はかなり揃えられていました。
今回はペイントなどで各座標を読み取ってベタ打ちで処理しています。
（ざっくりポイント②）
#買い入札量
df_buy_order = pd.DataFrame(np.where(np_img==1)).T
df_buy_order = df_buy_order[(df_buy_order[0]<=1000)]#右上の凡例を消す
df_buy_order[1] = df_buy_order[1] - df_buy_order[1].min()
df_buy_order[0] = df_buy_order[0] - df_buy_order[0].min()
df_buy_order[1] = df_buy_order[1]/(1166-162)*70000#x軸の最大値は70000MW
df_buy_order[0] = df_buy_order[0]/df_buy_order[0].max()*1000#y軸の最大値は1000円/kWh
#売り入札量
df_sell_order = pd.DataFrame(np.where(np_img==2)).T
df_sell_order = df_sell_order[(df_sell_order[0]<=1000)]#右上の凡例を消す
df_sell_order[1] = df_sell_order[1] - df_sell_order[1].min()
df_sell_order[0] = df_sell_order[0] - df_sell_order[0].min()
df_sell_order[1] = df_sell_order[1]/(1166-162)*70000#x軸の最大値は70000MW
df_sell_order[0] = df_sell_order[0]/df_sell_order[0].max()*1000#y軸の最大値は1000円/kWh
#買い入札量と売り入札量の可視化
plt.figure(figsize=(6, 5))
plt.scatter(df_sell_order[1],df_sell_order[0],s=0.1)
plt.scatter(df_buy_order[1],df_buy_order[0],s=0.1)
plt.ylim(ymin=0,ymax=1000)
plt.xlim(xmin=0,xmax=70000)
plt.legend(['売り入札量(kWh)','買い入札量(kWh)'])
plt.grid()
plt.show()
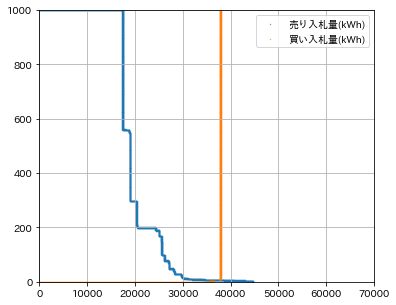
いい感じに画像の座標が取得できていそうです。
買い入札量に焦点を当てて見みます。
df_buy_order = round(df_buy_order, 2)
df_output_buy_order = df_buy_order.groupby(1).max()[0].drop_duplicates().reset_index()
df_output_buy_order.columns = ['累計売り入札量','入札価格']
df_output_buy_order['売り入札量'] = df_output_buy_order['累計売り入札量'].diff().shift(-1)
df_output_buy_order['累計売り入札量'] = df_output_buy_order['累計売り入札量'].shift(-1)
df_output_buy_order
| 累計売り入札量(MW) | 入札価格(円/kWh) | 売り入札量(MW) |
|---|---|---|
| 17500 | 1000 | 17500 |
| 17569.72 | 998.8 | 69.72 |
| 18127.49 | 561.45 | 557.77 |
| 18824.7 | 560.24 | 697.21 |
| 18894.42 | 559.04 | 69.72 |
| 19033.86 | 549.4 | 139.44 |
| 19103.59 | 548.19 | 69.73 |
| 20358.57 | 298.8 | 1254.98 |
| 20428.29 | 297.59 | 69.72 |
| 20498.01 | 209.64 | 69.72 |
| 20567.73 | 208.43 | 69.72 |
| 20707.17 | 201.2 | 139.44 |
| 24402.39 | 200 | 3695.22 |
| 24472.11 | 198.8 | 69.72 |
| 25099.6 | 190.36 | 627.49 |
| 25169.32 | 189.16 | 69.72 |
| 25587.65 | 169.88 | 418.33 |
| 25657.37 | 168.67 | 69.72 |
| 25727.09 | 149.4 | 69.72 |
| 26215.14 | 100 | 488.05 |
| 26284.86 | 98.8 | 69.72 |
| 27051.79 | 79.52 | 766.93 |
| 27121.51 | 78.31 | 69.72 |
| 27191.24 | 71.08 | 69.73 |
| 27260.96 | 69.88 | 69.72 |
| 28097.61 | 49.4 | 836.65 |
| 28167.33 | 48.19 | 69.72 |
| 28237.05 | 42.17 | 69.72 |
| 28306.77 | 39.76 | 69.72 |
| 28376.49 | 38.55 | 69.72 |
| 28446.22 | 34.94 | 69.73 |
| 29701.2 | 30.12 | 1254.98 |
| 29770.92 | 28.92 | 69.72 |
| 29840.64 | 25.3 | 69.72 |
| 29910.36 | 20.48 | 69.72 |
| 30049.8 | 19.28 | 139.44 |
| 30119.52 | 18.07 | 69.72 |
| 30189.24 | 15.66 | 69.72 |
| 30816.73 | 14.46 | 627.49 |
| 31235.06 | 13.25 | 418.33 |
| 32001.99 | 12.05 | 766.93 |
| 34093.63 | 10.84 | 2091.64 |
| 34721.12 | 9.64 | 627.49 |
| 35557.77 | 8.43 | 836.65 |
| 38625.5 | 7.23 | 3067.73 |
| 40786.85 | 6.02 | 2161.35 |
| 43157.37 | 4.82 | 2370.52 |
| 44621.51 | 3.61 | 1464.14 |
| 44760.96 | 2.41 | 139.45 |
| NaN | 1.2 | NaN |
| 特徴として、1000円、560円前後、300円前後、200円、190円前後、170円前後、100円、80円前後、50円前後、30円前後に大きい買い入札が入っていることがわかります。また、この日のシステムプライスは7.72円/kWhだったのですが、価格の前後に多くの入札が入っていることもわかります。（ざっくりと変換しているため、誤差が伴っている点注意です。） |
7.72円以上で入札した場合はめでたく7.72円で約定し、7.72円未満で入札した場合は取引出来ず、といった世界だと思われるので、入札量と金額に関するデータは意思決定において有用なのではないかと思います。
入札量の時系列推移など引き続き見ていき、入札行動に変化が生じていないかなど、深堀りを続けていきたいと思います。
#おわりに
プロットエリアの座標やメモリの最小最大値など、画像の形式がかなり揃えられているのを良いことに、所々ベタ打ちの箇所があります。また、色の座標を読み取ってその一部を代表値として用いていたり、かなりざっくりと変換しています。
これらの精緻化も追々行いたいと思います。