だいぶ前にFPGAで作ったアルゴリズムをメモとして書いておきます。
概要
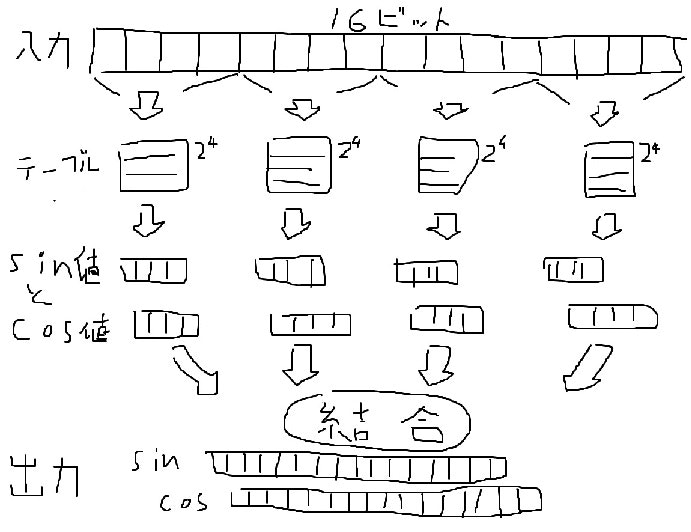
入力角度をテーブル参照を使って求めています。
テーブル参照というのは、メモリ内にsin値、cos値をあらかじめテーブルとして用意しておいて、角度が入力されたときに、テーブルからsin値、cos値を返す方法です。
下記のようにメリット・デメリットがあります。
メリット
・演算がないため処理が高速
・簡単に作れる
デメリット
・精度を高めるほどメモリを食う
テーブルを分割しよう
上のデメリットはテーブルを分割することで緩和できます。
テーブルを分割すると、参照した値を結合するための演算が増える代わりに、必要なデータ数を大幅に削ることができます。
データ量=2^(入力のビット幅)×出力のビット幅
入力、出力を2Byteとすると、テーブルのサイズは128kByteになります。大きいですね。
分割した場合のデータサイズは下記のようになります。
データ量=2^(入力のビット幅/分割数)×出力のビット幅*分割数
例えば、テーブルを4分割するとテーブルのサイズは128Byteまで縮小します。
精度をほぼ落とさずに1/1024に縮小できます!
データの結合しよう
上で少し触れましたがテーブルを分割するとテーブルから参照したデータを結合する必要があります。
なぜなら、分割したテーブルから参照した値は元々の入力値の三角関数値ではないからです。
それぞれのテーブルから参照した値を結合する必要があります。
結合には加法定理を使います。
・sin(α+β)=sin(α)cos(β)+cos(α)sin(β) ・cos(α+β)=cos(α)cos(β)-sin(α)sin(β)
加法定理を使って、それぞれの参照値を結合していきます。
結合回数はテーブルを分割するほど増えるので注意です。
FPGAで掛け算しようとすると結構処理数が増えるので、あまりテーブルを分割するのも考え物です。
ちなみに、4分割すると結合数は3回になります。
まとめ
テーブル参照を使うことで、処理の軽い三角関数値アルゴリズムを作ることができます。
ですが、精度を高めるほどに使用するメモリが指数関数的に増えていくので、
テーブル分割などのサイズを縮小する対策を考える必要があると思います。
実際には、分割によるデータサイズの削減と結合回数の増加を天秤にかけながら、分割数を決めることになります。