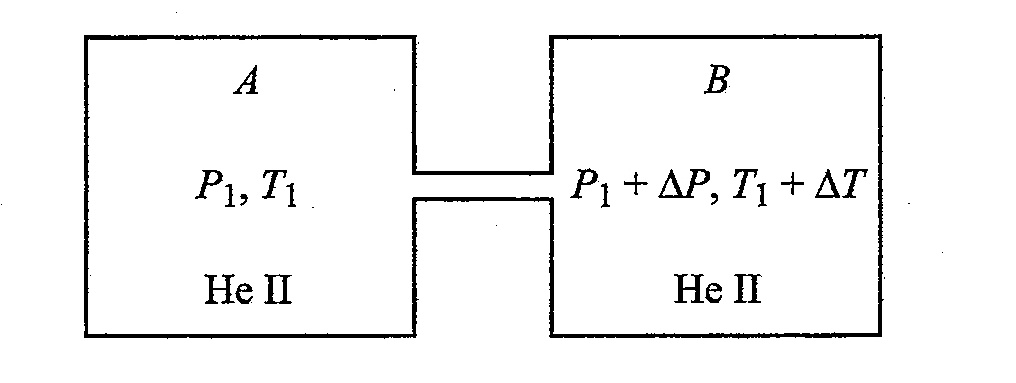$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\Braket#1{\mathinner{\left\langle{#1}\right\rangle}}
$$
液体ヘリウムに魅せられて
みなさんこんにちは、Kuruといいます。12月も中旬に入り、かなり寒くなってきましたね。寒いと言えば低温、低温といえば超流動ですよね(?)。ということでここでは超流動について、特に皆さんご存知のヘリウムについてほんの少し記事を書こうと思います(今年は真面目な記事が多いということで、「クレイジーすぎるRTA10選!」とか、「ゼルダの伝説各作品の推しポイント!」とか、「ジョジョ立ちについてッ!!」みたいな誰得記事を書いても良かったんですが、HeIIについて書くと最初に行ってしまったので真面目な記事にしました)。まず、ヘリウムには安定同位体が二つあり、一つは原子核が陽子二つと中性子二つからなるヘリウム4で、もう一つは原子核が陽子二つと中性子一つからなるヘリウム3です。当然、ヘリウム4はボソン、ヘリウム3はフェルミオンです。ヘリウム3にもフェルミオンに特有の大変面白い性質があるのですが、ここではボソンであるヘリウム4に話を絞ります。
序論
ボソンであるヘリウム4は、1907年にKamerlingh Onnesによって液化され、以降いわゆる低温物理学に欠かせない存在となりました。しかし、Onnesが液化して以降、ヘリウム4そのものには(少なくとも私が知る限り)劇的な発展はなく、今回私が話す超流動の発見には Pyotr Kapitsaの1937年の実験まで待たねばなりませんでした。Kapitsaは、温度2.18Kで液体ヘリウム4の沸騰が止まり、静かな別の相に転移することを見出したのです(風の噂ではOnnesは既に超流動ヘリウムを冷却によって得ていたが、それに気づかなかったらしい)。この状態をHeIIと呼びます(ただの液体ヘリウム4をHeIと呼びます)。転移点で比熱は発散し、その形状はギリシャ文字λに似ていることからλ点と呼ばれます。ヘリウム4はボソンであるため、(ヘリウムが理想ボース気体だとすれば)極低温ではBose-Einstein凝縮が起こると予想されます。実際、ヘリウム4は理想ボース気体であると仮定してBose-Einstein凝縮の転移温度を計算すると(転移温度は密度に依存するので一意には定まりませんが)ある密度に対してその転移温度はλ点の実測値2.18Kに近い値になります。しかし、転移点近傍の比熱の振る舞いは、ヘリウム4が理想ボース気体だと仮定すると説明できません。実際、理想ボース気体の転移点以下での比熱の振る舞いは
$$
C_{\mathrm{ideal}} \propto T^{3/2}
$$
になりますが、実験では
$$
C_{\mathrm{experiment}} \propto T^{3}
$$
です。これは看過できません。すなわち、ヘリウム4は理想Bose気体ではないということを表しています(これに関連して、相互作用を操作できるほとんど理想的なボース気体での凝縮として1995年でのレーザーによる冷却現象があります。これも非常に面白い話題ではありますが、ここでは省略します)。もちろん、何らかの形でBose-Einstein凝縮が関わることは間違い無いと考えられています。実は、λ点以下で比熱が
$$
C \propto T^{3}
$$
と振る舞うことは(現象論的には)理解されています。これはFeynmanによって説明されました。
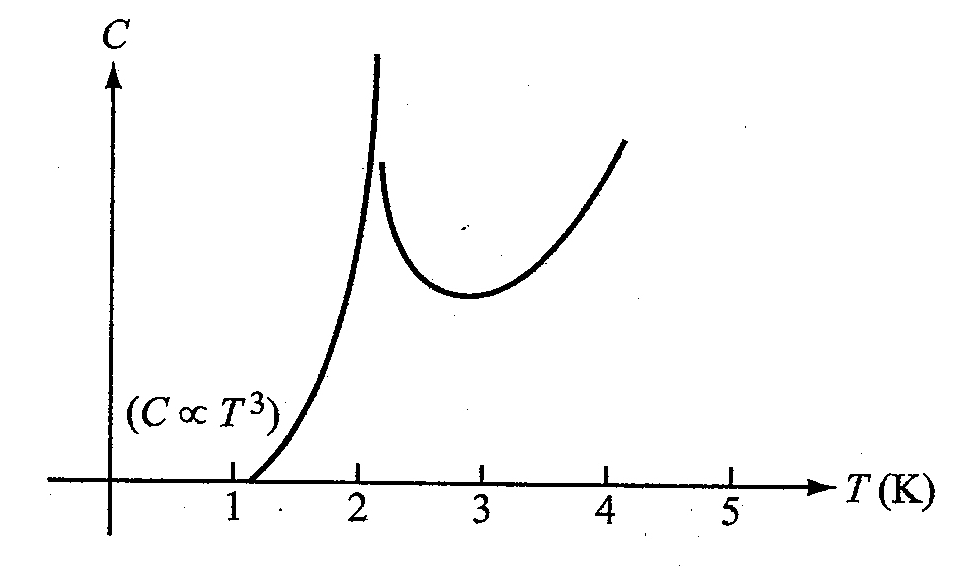
図1 ヘリウム4のλ点。
HeIIの種々の性質
HeIIには種々の非常に面白い性質があります。いくつか列挙すると:
- HeIIは蒸発はするが沸騰はしない。これは熱伝導率が無限大であると説明される。
- 粘性が(ある条件下で)0である。ある臨界速度$V_{\mathrm{c}}$以下で、HeIIは抵抗ゼロで毛細管を流れる。これはHeIIの粘性が0であることを示唆する。しかし、シリンダーを液体ヘリウム内部に設置してシリンダーを回転させると、シリンダーからHeIIに角運動量が移動する。これはHeIIの粘性が0では無いことを示唆する。これらの結果から、定性的には、HeIIは粘性0の超流動成分と、粘性が0ではない常流動性分の完全な混同体であると言える。観測データを再現するには、常流動性分の「密度」$\rho_{\mathrm{n}}$と超流動成分のそれ$\rho_{\mathrm{s}}$の比は温度依存性を持つと仮定しなければならない(Landauの相転移理論に従うと考えれば、秩序パラメータがこの比に相当しそうだとわかりますね。実際にはあまりうまくいきませんが。)。
- 熱機械効果あるいは噴水効果、そして機械熱効果(名前が似ていてややこしい:後者はmechano-chaloric effectという)。
二つの容器が毛細管で繋がれていて、内部はHeIIで満たされているとします。
図2 熱機械効果の概略図。
二つの容器内部それぞれでのHeIIの密度$\rho$と温度$T$は一定であるとします。すると、毛細管を通じて圧力差$\Delta P$が$\Delta P = \rho s \Delta T$になるまで超流体は流れます($s$は単位質量当たりのエントロピーです)。温度差によって圧力差が起こるこの現象を熱機械効果と呼びます。この熱機械効果の応用として、次のような状況を考えます。
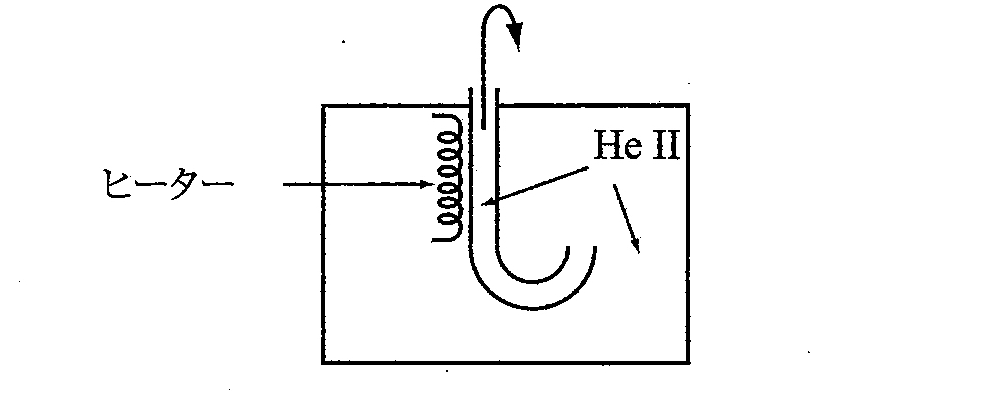
図3 噴水効果の概略図。
もし、一方の容器が細い管であれば、超流体は管を通じて移動し、外に出ていきます。これが噴水効果です。噴水効果は素晴らしい動画があるのでそちらを見てもらうことにしましょう。
図2のそれぞれの容器内の圧力を一定に保ち、AからBに質量が流れるとすると、容器Bは冷却されます(実験事実)。これを機械熱効果と呼びます。この現象は、流れたHeIIのエントロピーが0であるとすると定性的に説明できます。すなわち、容器B内のHeIIが増加するに従い、容器B内の単位質量あたりのエントロピーが減少するため温度が減少します。
他にも、ビーカーに入れたHeIIはビーカーの側面を伝わって出ていく現象もあります。一般に液体はvan del Waals力によって、ビーカーの側壁との間に高さの上昇とともに厚さが減少する液体層が形成されることが考えられますが、実際は側壁と液体のわずかな温度差とそれによる蒸気圧の差によって液体層は形成されません。しかし、HeIIは熱伝導率が実質的に無限大であるためにこの温度差が生じず、したがって液体層が形成されてビーカーの側壁を這って出ていきます。
このような「超流動」的な性質のほとんどは、HeIIの粘性が0,かつエントロピーも0であるとすると説明できます。
Landauの二流体モデル
以上の議論で、HeIIの性質は大雑把には二流体モデルで説明されることがわかりました。二流体モデルによる現象論的な理論は、1940年にTiszaが、1941年にLandauによって導入されました。実験と一致する結果を示したのはLandauの理論だったので、ここではLandauの理論を見てみることにします。
HeIIが、エントロピー、粘性共に0の完全流体と、ある励起(とりあえずフォノンだとする)からなるとしましょう。励起がフォノンならば、図1の比熱曲線と一致します。また、完全流体は粘性がないため毛細管を流れますが、フォノンは壁に衝突するため毛細管を流れません。すなわちフォノンは粘性を持つことになります。この二流体モデルは、Andronikashviliの実験によってさらに説得力が増しました。彼は、複数の円盤を少しずつ間隔を開けて回転軸に固定し、それをHeII中で回転させました。このとき、超流動成分は粘性が0なので影響を受けませんが、励起している常流動性分は粘性を持つため慣性による影響を受けます。これを観測すると次のようになりました。
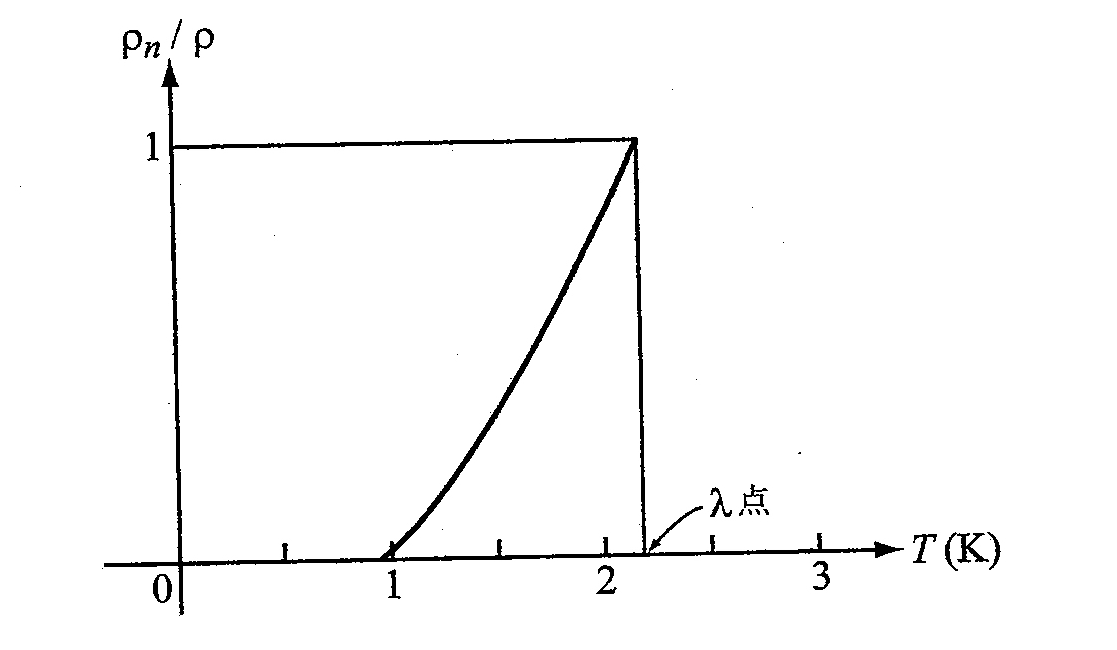
図4 Andronikashviliによる実験の結果。横軸が温度m縦軸が常流動成分の「密度」を表す。
この二流体モデルに基づくと、HeIIの任意の位置において全密度は本質的に一定ですが、超流動成分と常流動成分の比は異なっていると考えられます。一方、励起の密度は温度に依存するので、$\rho_{\mathrm{n}}/\rho$が変われば温度も必ず変化します。これより、「第二音波」として知られる波の伝搬が引き起こされます。第二音波は温度の波で、圧力によって引き起こされる通常の音波(第一音波)とは区別されます。
Landauの二流体モデルでは、第二音波はフォノン気体の密度波と考えることができます。一般に、粒子の速度が$C$のとき、音速は$C/\sqrt{3}$となることが知られているので、絶対零度近傍でのフォノンの速度を$c$とすると第二音波の速度は$c_{\mathrm{s}}=c/\sqrt{3}$となります。Tiszaは絶対零度近傍で$c_{\mathrm{s}}$は0になると予想しました。実験結果はLandauの理論を支持していました。
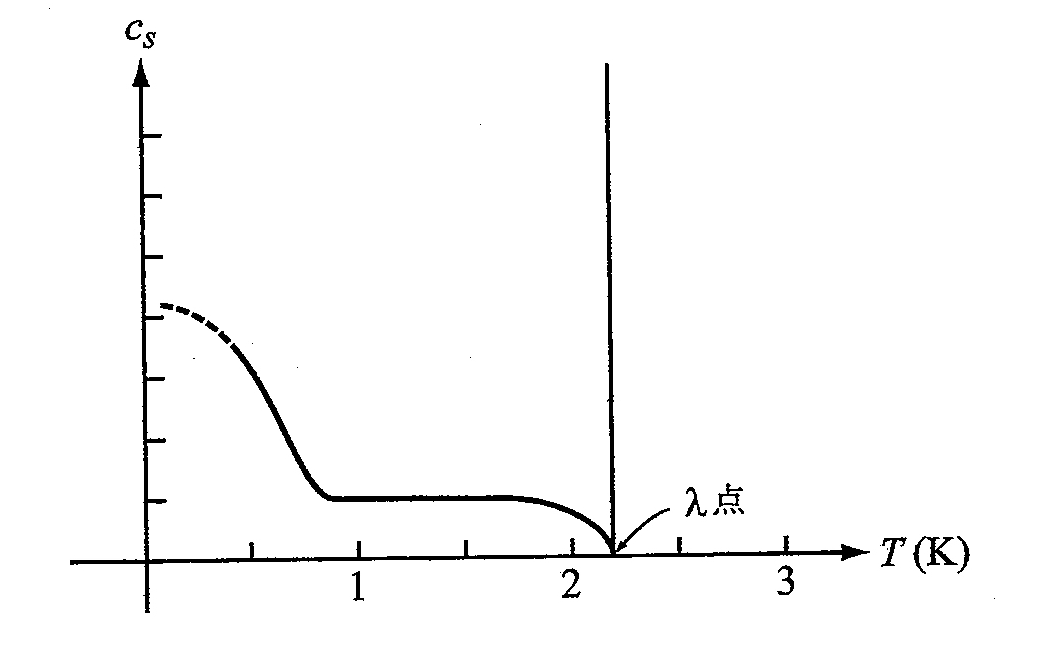
図5 第二音波の温度依存性。横軸が温度、縦軸が第二音波の速度を表す。
第二音波については
https://www.youtube.com/watch?v=NjPFfT2EyxQ
を参照してください。
実際には図5のような温度依存性が第二音波にはあり、Landauの予想は1K以下の極低温でのみ成り立っています。1Kからλ点近傍での第二音波の性質を説明するには、フォノン以外の励起が必要です。
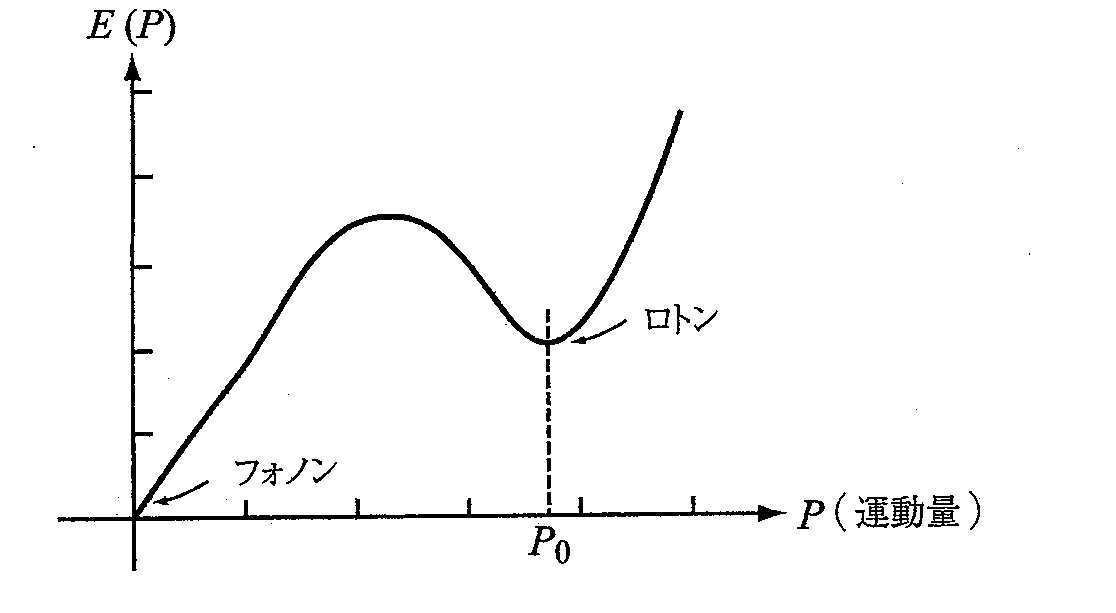
図6 エネルギーの運動量依存性(分散関係)。横軸が運動量、縦軸がエネルギーを表す。
図6はエネルギーの運動量依存性の実験結果を表していて、ある運動量$P_{0}$に極小点があります。この励起をLandauはロトンと呼びました。この励起曲線を基にLandauは理論を展開しました。
極低温では励起はフォノンであり、$E(P) = cP$と表せます。一方、ロトン励起の近傍では
$$
E(P) = \Delta + \frac{P-P_{\mathrm{0}}}{2\mu}
$$
とかけます($\Delta$は何らかの定数で、$\mu$は何らかの有効質量です)。これらのエネルギーの表式から、より定量的な議論が可能です。
エネルギーを計算してみましょう。フォノン由来のエネルギーの期待値は、フォノンがボソンであることから
$$
E_{\mathrm{ph}} = \int_{0}^{\infty}\frac{cP}{e^{cP/k_{\mathrm{B}}T}-1} \frac{4\pi P^{2}dP}{(2\pi\hbar)^{3}} = \frac{4\pi^{5}k_{\mathrm{B}}^{4}T^{4}}{15h^{3}c^{3}}
$$
となり、その比熱は
$$
C_{\mathrm{ph}} = \frac{16\pi^{5}k_{\mathrm{B}}^{4}T^{3}}{15h^{3}c^{3}}
$$
となります。また、ロトンのエネルギーは、エネルギーが大きくなるとBose分布はBoltzmann分布で近似できる($\Delta$の存在によってこれが常に成り立つと言える)ことから、
$$
E_{\mathrm{rot}} = \int_{0}^{\infty}\left[\Delta + \frac{(P-P_{0})^{2}}{2\mu}\right]e^{-\Delta/k_{\mathrm{B}}T}e^{-\beta(P-P_{0})^{2}/2\mu k_{\mathrm{B}}T} \frac{4\pi P^{2}dP}{(2\pi\hbar)^{3}}
$$
となります。地道に計算し(ぜひやってみてください)、比熱を求めると
$$
C_{\mathrm{rot}} = \frac{2\sqrt{\mu}P_{0}^{2}\Delta^{2}}{(2\pi)^{3/2}\sqrt{k_{\mathrm{B}}}T^{3/2}\hbar^{3}} \left[1 + \frac{k_{\mathrm{B}}T}{\Delta} + \frac{3}{4}\left( \frac{k_{\mathrm{B}}T}{\Delta}\right)^{2} \right] e^{-\Delta/k_{\mathrm{B}}T}
$$
となります。積分の際、$P=P_{0}$の部分が主に寄与することから$P=P_{0}$と置き換えても問題ありません。また、積分区間は$0$からではなく$-\infty$からとしても差し支えない(主な寄与ではないため)ことを利用しています。
次に、超流動部分が運動している時の励起エネルギーを考えてみましょう。超流動成分の速度を$\boldsymbol{V_{\mathrm{s}}}$とすると、励起エネルギーは
$$
E = E(\boldsymbol{P}) + \boldsymbol{P}\cdot \boldsymbol{V_{\mathrm{s}}}
$$
となります。これを簡単に理解するには、次のように考えればよいでしょう。ある運動量$\boldsymbol{P}$の励起が生成されたとします。ただし、その大きさ$P$は十分小さいとします。このとき、励起によって流体全体は$\boldsymbol{P}/M$の運動量を失います($M$は流体全体の質量です)。励起ができる前後でエネルギーが保存していると考えると、全エネルギーは
$$
\frac{M}{2}\left( \boldsymbol{V_{\mathrm{s}}} +\frac{\boldsymbol{P}}{M}\right)^{2} + E(\boldsymbol{P}) \simeq \frac{MV_{\mathrm{s}}^{2}}{2} + \boldsymbol{P}\cdot\boldsymbol{V_{\mathrm{s}}} + E(\boldsymbol{P})
$$
とかけます(ただし$P^{2}$の項は無視しました)。励起がない時の流体のエネルギーは$MV_{\mathrm{s}}^{2}/2$なので、励起エネルギーは
$$
E = E(\boldsymbol{P}) + \boldsymbol{P}\cdot \boldsymbol{V_{\mathrm{s}}}
$$
となることがわかりました。全運動量密度は
$$
\rho\boldsymbol{V_{\mathrm{s}}} + \Braket{\boldsymbol{P}}
$$
で与えられることに着目します。$\Braket{\boldsymbol{P}}$は、フォノンがボソンであることから
$$
\begin{align}
\Braket{P} &= \int\frac{\boldsymbol{P}}{\exp{[(E(\boldsymbol{P}) + \boldsymbol{P}\cdot \boldsymbol{V_{\mathrm{s}}})/k_{\mathrm{B}}T}]-1}\frac{d^{3}\boldsymbol{P}}{(2\pi\hbar)^{3}} \
&= -\int\frac{\boldsymbol{P}(\boldsymbol{P}\cdot\boldsymbol{V_{\mathrm{s}})}/k_{\mathrm{B}}e^{E(\boldsymbol{P})/k_{\mathrm{B}}T}}{(e^{E(\boldsymbol{P}/k_{\mathrm{B}})T}-1)^{2}} \frac{d^{3}\boldsymbol{P}}{(2\pi\hbar)^{3}}
- O{(V_{\mathrm{s}}^{2})} \
&= -\rho_{\mathrm{n}} V_{\mathrm{s}}
\end{align}
$$
となります(Taylor展開:
$$
f(x+a) = f(x) + \frac{\partial f}{\partial x} a + O(x^{2})
$$
に基づいています)。ここで、
$$
\rho_{\mathrm{n}} = \int\frac{(P^{2}/3k_{\mathrm{B}}T)e^{E(\boldsymbol{P})/k_{\mathrm{B}}T}}{(e^{E(\boldsymbol{P})/k_{\mathrm{B}}T}-1)^{2}}\frac{d^{3}\boldsymbol{P}}{(2\pi\hbar)^{3}}
$$
と定義されています(被積分関数の分子が少し変わったのは、適当に座標軸を取り直して、各座標軸方向の平均をとったことによります)。ここで、$\rho_{\mathrm{n}}$というのは現実での密度を指すわけではないことに注意してください。上での計算と定義から、全運動量密度について
$$
(\rho - \rho_{\mathrm{n}})\boldsymbol{V_{\mathrm{s}}} = \rho_{\mathrm{s}}\boldsymbol{V_{\mathrm{s}}}
$$
と書けるでしょう。つまり、励起によって、全体の流れがいわば阻害されていると解釈できます。これは常流動成分の特徴と言えます。
基底状態の探索
今まで、フォノンが極低温でのHeIIの励起を支配していると考えていたわけですが、これはあくまで実験と合うように現象論的に考えていただけに過ぎません。多体問題としてHeIIを考察して、実際にフォノンが極低温での励起になっていることを示したいわけです。以下ではFeynmanの議論を少しだけみましょう。
一般に、基底状態の波動関数は節を持たず、励起状態になると節の数が増えていきます。基底状態の波動関数を$\varphi$、第一励起状態のそれを$\psi$としましょう。基底状態で波動関数は節を持たないため$\varphi$は常に正で、第一励起状態では全ての配位のうち半分で正、残り半分で負になります。また、直交性から
$$
\int \varphi\psi d^{3N}\boldsymbol{R} = 0
$$
が成り立ちます。ここでフォノンの特徴を考えます。フォノンは圧縮による励起状態、すなわち密度の変化をもたらす各原子の小さな変位を伴った状態です。フォノンが小さいエネルギーを持つためには、密度の揺らぎが長距離にわたる(波長が長い)必要があります。なぜなら、一つのフォノンのエネルギーはご存知の通り$\hbar\omega$で、$\omega$は
$$
\omega = \frac{2\pi c}{\lambda}
$$
と書けるからです($c$は音速です)。波長$\lambda$が大きければフォノンのエネルギーが小さくなることがわかります。ここから、問題はフォノン以外の状態がなぜこのような低いエネルギーを持たないかということだということです。
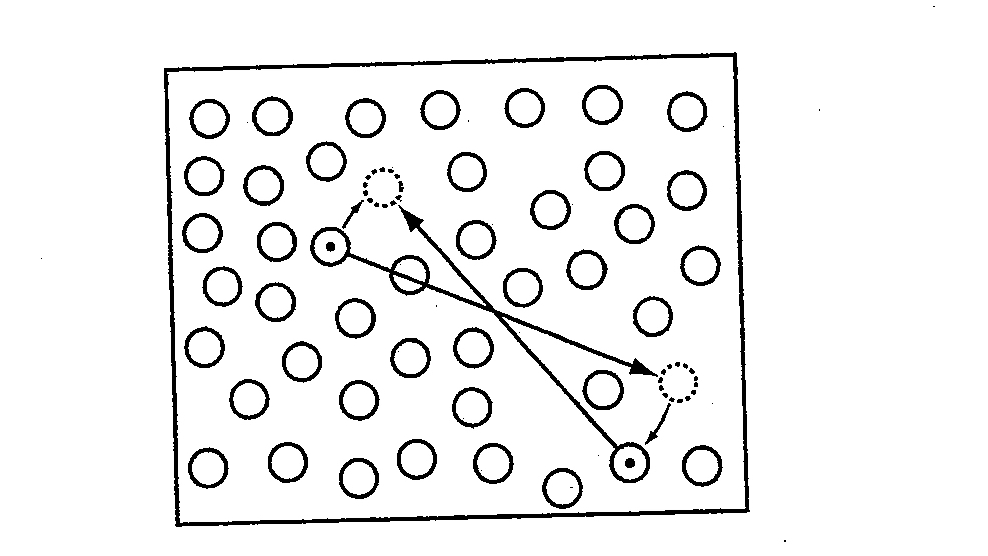
第一励起状態$\psi$がフォノン由来でないとしましょう。すると、$\psi$は$\varphi$およびフォノン由来の励起状態と直交していなければなりません。これは、$\psi$が大域的な密度の変化を伴わないような粒子の配置の変化によってその値が正から負に変わらなければならないということです。仮定から$\psi$は非常に小さいエネルギーを持っていなければならないので、正から負への変化は非常に緩やかでなければなりません(緩やかでなければ、空間変動$\nabla\varphi$に由来するエネルギーが大きくなってしまいます)。したがって粒子は長距離の配位の変化を伴わなければなりませんが、これは不可能です。なぜなら、ヘリウム4はボース粒子であり、同種粒子は区別できないので、長距離の配位の変化を伴うようなものは、別の「近い」粒子のわずかな配位の変化によって達成されるからです。
図7 フォノン由来の励起しか不可能な理由を表す概略図。ある原子の長距離の配位の変化によって達成される新たな配位は、別の「近い」原子のわずかな配位の変化によっても達成されうる。
これで、基底状態からの低エネルギー励起がフォノンしかあり得ないことがわかりました。
Feynmanは凄まじい物理的直感と変分原理によって図6のようなスペクトルの概形を導くのですが、長くなるのでここでは省略します。概略だけ示すと、$\psi$を
$$
\psi = \exp{\left( \sum_{i}f(\boldsymbol{R_{i}} )\right)}\varphi
$$
と書き($\boldsymbol{R}_{i}$は$i$番目の原子の位置)、部分積分を用いて中性子散乱の構造因子$S{(\boldsymbol{K})}$と一原子の励起エネルギー$\epsilon$を
$$
\epsilon = \frac{\hbar^{2}K^{2}}{2mS(\boldsymbol{K})}
$$
と結びつけました。中性子の構造因子は実験から求められるので、それから励起エネルギーのスペクトルがわかる、という算法です。この論法でフォノン領域のスペクトルはほとんど再現できるのですが、ロトン領域のスペクトルは(極小点は出てくるのですが)残念ながら完全には再現できませんでした。
また、ここで得た波動関数は確率の密度を保存しないので、
$$
\psi = \left( \sum_{i}\exp{\left[ \mathrm{i}\boldsymbol{K}\cdot\boldsymbol{R_{i}} + \sum_{j\neq i}f(\boldsymbol{R_{j}} - \boldsymbol{R_{i}}) \right]} \right)\varphi
$$
という形を仮定し、再び変分原理によって
$$
\psi = \sum_{i}e^{\mathrm{i}\boldsymbol{K}\cdot\boldsymbol{R_{i}} + \sum_{j}f(\boldsymbol{R_{j}} - \boldsymbol{R_{i}})} \simeq \sum_{i}e^{\mathrm{i}\boldsymbol{K}\cdot\boldsymbol{R_{i}}}\left[ 1 + \alpha\sum_{j\neq i}\frac{\mathrm{i}\boldsymbol{K}\cdot(\boldsymbol{R_{i}} - \boldsymbol{R_{j}})}{|\boldsymbol{R_{i}} - \boldsymbol{R_{j}}|^{3}} \right]\varphi
$$
という形を得ました。
流れがある時の超流動
HeII全体が一様に速度$\boldsymbol{V}$で運動しているとすると、この時の波動関数は
$$
\varphi = \exp{\left( \mathrm{i}\frac{m}{\hbar}\sum_{i}\boldsymbol{V}\cdot \boldsymbol{R_{i}} \right)}\varphi
$$
となります。位相因子は、
$$
m\boldsymbol{V}\cdot \sum_{i}\boldsymbol{R_{i}} = Nm\boldsymbol{V}\cdot\left( \sum_{i}\frac{\boldsymbol{R_{i}}}{N} \right) = \boldsymbol{P_{\mathrm{total}}}\cdot\boldsymbol{R_{\mathrm{cm}}}
$$
とかけます。ここで、$\boldsymbol{P_{\mathrm{total}}}$は系全体の運動量、$\boldsymbol{R_{\mathrm{cm}}}$は系の重心座標です。すなわち、系全体の運動量による位相の変化とみなせます。
実際は、系全体で速度が一様ではなく、各点で速度は異なるでしょう。そこで、各点の速度場に由来する位相を$\theta(\boldsymbol{R_{i}})$として、波動関数を
$$
\varphi = \exp{\left[ \mathrm{i}\sum_{i}\theta(\boldsymbol{R_{i}}) \right]}\varphi
$$
と書きます。各点の速度場は、$\theta(\boldsymbol{R})$から
$$
\boldsymbol{V}(\boldsymbol{R}) = \frac{\hbar}{m}\nabla\theta(\boldsymbol{R})
$$
と定まります。超伝導での磁束の量子化でもあるように、系が単連結なら$\nabla \boldsymbol{V}\times(\boldsymbol{R}) =\boldsymbol{0}$となるので、渦なし流れとなります。しかし、例えば系の中心に穴がある場合(円筒を思い浮かべてください)、循環する速度場$\boldsymbol{V}$が可能です。このとき、$k$を定数として
$$
\theta = k\Theta
$$
とします($\Theta$は円筒座標系での回転角です)。すると
$$
V = \frac{\hbar k}{mr}
$$
とかけますが、波動関数が一価でなければならないという制約から
$$
\begin{align}
\theta &= n\Theta, \
V &= \frac{\hbar}{mr}n,
\end{align}
$$
および
$$
\oint\boldsymbol{V}\cdot d\boldsymbol{s} = 2\pi\frac{\hbar}{m}n
$$
となります($n$は整数です)。これは渦糸が量子化されたことに他なりません。この議論はOnsagerによって提案されました。位相に対する条件によって量子化される例の一つですね。Feynmanはこの議論をさらに発展させて、渦糸をいかに導くか、も議論しました。量子化された渦糸は実験でも観測されています。
ヘリウム4のλ転移
今までは転移温度よりも十分温度が低いと仮定して議論をしてきたわけですが、転移点近傍になると図6のような$E-P$曲線は破綻します。転移点では異なったアプローチが必要だということです。Feynmanは経路積分を用いて議論を進めましたが、長くなるので省略します。結果だけ記すと、転移点での比熱の発散は導けませんでした。その後、様々な偉人達がこのλ転移に挑みましたが、完全な解決には至っていません。Matsubara(温度グリーン関数を導入したのと同じ人)は格子気体模型に基づいて転移の存在を導きましたが、転移に議論を絞っており、完全な理論とは言えません。まだまだこの謎は解決されないでしょう。
終わりに
今までHeIIの種々の性質を(かなり省略しながら)書いてきましたが、個人的にはまだまだ魅力的な問題がたくさんある、という印象です。ここでは触れませんでしたが、相互作用のほとんどないボース気体のレーザー冷却、およびその系の振る舞いや、HeIIの乱流、圧力をかけた固体HeIIといったものもありますし、フェルミオンであるヘリウム3の問題もあります。また、ここで触れた内容でも、比熱曲線の完全な理論的導出、一原子あたりの励起エネルギー曲線といった問題も残っています。今回どなたかがこの記事を読んで興味を持ってくれれば幸いですし、さらにこのような問題を解いていただければ非常に喜ばしいです。
注
この記事の図はすべて『ファインマン統計力学』に依っています。
参考文献
R.P.ファインマン著、西川恭治監訳、『ファインマン統計力学』、丸善出版(2009)
今回の記事はこの本にほとんど依っている。
L.D.Landau, J. Phys. USSR $\boldsymbol{5}$, 71 (1941).
E.L. Andronikashvili, J. Phys. USSR $\boldsymbol{10}$, 201 (1946); *Zh, Experim. i Teor. Fiz * $\boldsymbol{18}$, 424 (1948).
R.P.Feynman, Phys. Rev. $\boldsymbol{91}$, 1291, 1301 (1953); $\boldsymbol{94}$, 262 (1954).
R.P.Feynman and M.Cohen, Phys. Rev. $\boldsymbol{102}$, 1189 (1956).
L.Onsager, Nuovo Cimento $\boldsymbol{6}$, Suppl. 2, 246(1949).
T.Matsubara and H. Matsuda, Progress of Theoretical Physics, $\boldsymbol{16}$, 6 (1956); $\boldsymbol{17}$, 1 (1957).