はじめに
おはようございます。
記事を書いているのは夜ですが、おはようって言ってみました。
MYJLab Advent Calendar 2023の13日目です。担当のセイです〜!
11日目の記事も担当させていただきましたが、あげたのが12の夜でした。遅くなってしまい申し訳ありませんでした。
でも、こういう平気に学校行事の締め切るをやぶる感じ、僕っぽいじゃ僕っぽいですね。(<- こいつ反省する気ゼロ)
みんなすごく頑張ってくれているので、今回の記事は間に合うといいですね。
今回のテーマについて
今回のテーマは「動的計画法(Dynamic Programming, DP)」です。
ゼミで『世界標準MIT教科書 Python言語によるプログラミングイントロダクション 第3版』の本を輪講をしていますが、その中の15章動的計画法を担当しました。
競プロで一度DPのことを勉強して、一応使えはしますが、この本はすごく正当派な方式でDPを説明しているので、いろいろと勉強になりました。
なので、今回の記事もこの本の15章をベースに書いていきます。出している図表もコードサンプルもこの本のものを使っています。
なお、フィボナッチ数例問題や0/1ナップサック問題が出てきますが、簡単の説明しかしないので、知らない方は調べてくださいね。
動的計画法とは?
ここはまず概念的な話をします。
動的計画法は、1950年、リチャード・ベルマンによって提唱された、部分問題の重複性と部分構造の最適性という特徴を明らかにすることによって、最適化問題を効率的に解くための解法である。
運が良いことに、多くの最適化問題はこれらの特徴を顕している。
とのことです。
部分構造の最適性
大域的な最適解が部分問題の最適解を組み合わせることによって得られる場合、その問題は部分構造の最適性(optimal substructure)を持つという。
部分問題の重複性
最適解を得るために同じ問題を何度も解く必要があるとき、その問題は部分問題の重複性(overlapping subproblems)を持つという.
と本の中では説明されている。まぁ、概念だけではわかりにくいので、実際に例を見ていこう。
フィボナッチ数列の例
問題の解析
例えば、フィボナッチ数列問題は部分構造の最適性と部分問題の重複性の両方を持つ。
フィボナッチ数列は一般的に以下のように定義される。
F(n) =
\begin{cases}
0 & \text{if } n = 0 \\
1 & \text{if } n = 1 \\
F(n-1) + F(n-2) & \text{if } n > 1
\end{cases}
式でわかるように、この問題には、部分構造の最適性を持つ。つまり、最適解が部分問題の最適解を組み合わせることによって得られる。
では、部分問題の重複性はどうはどうなのか?
解決例を見てみよう。
フィボナッチ数列の問題をとくためには、典型的な再帰関数を使う方法がある。
def fib(n):
"""Assumes n is an int >= 0
Returns Fibonacci of n"""
if n == 0 or n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
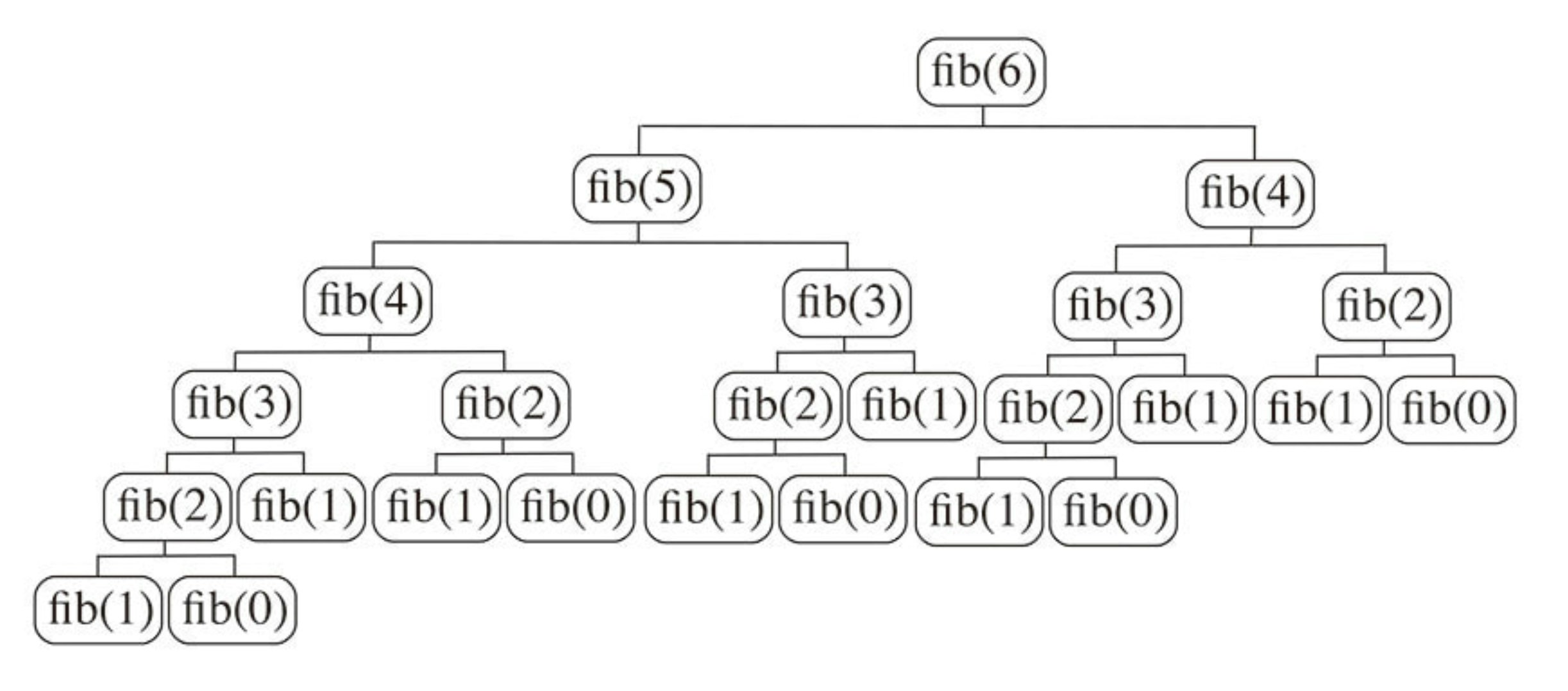
これでも分かりにくいので、fib(6)を実行するときの関数呼び出しのツリーを見てみよう。
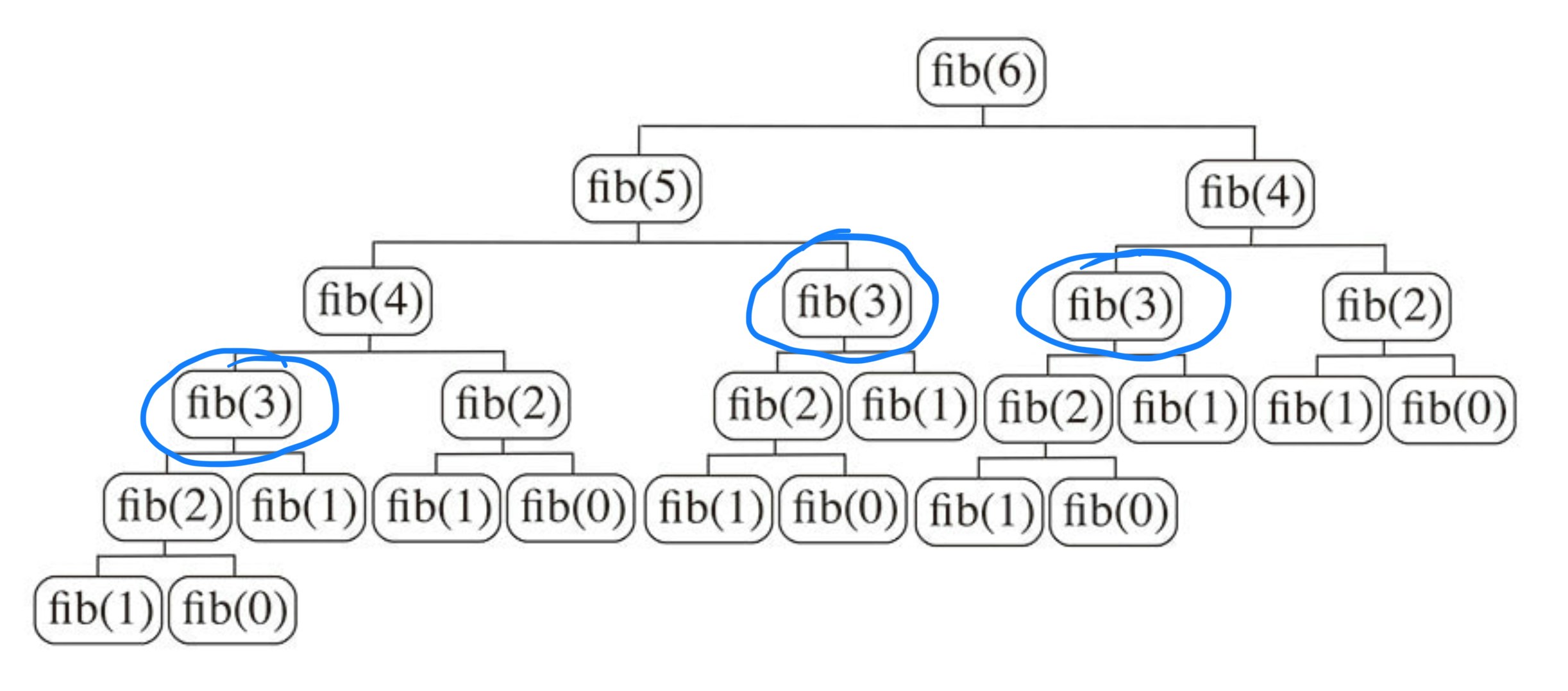
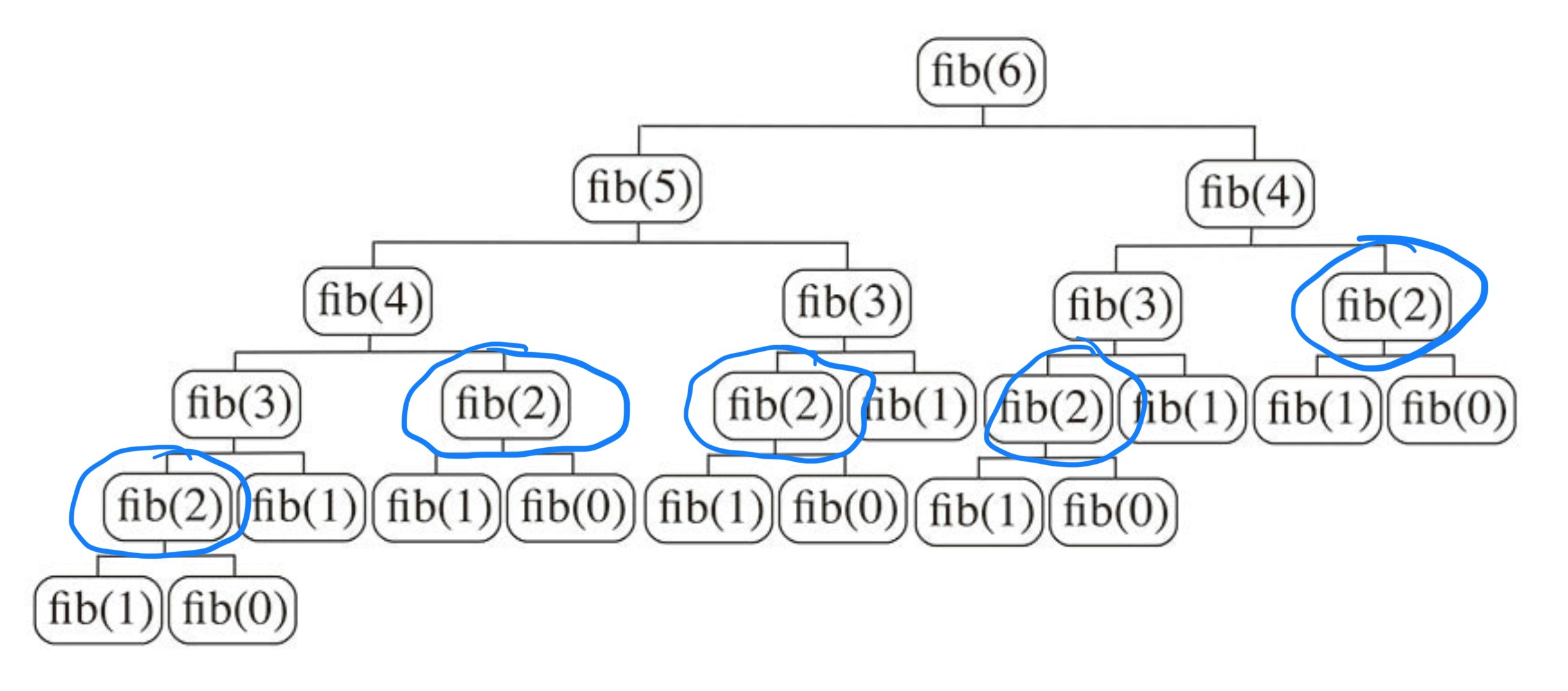
図でわかるようにfib(3)は三回fib(2)は五回呼び出されている。最適解を得るために同じ問題を何度も解く必要があるので、この問題は部分問題の重複性を持つということがわかる。
計算量を考えてみると、精密に導き出すのは難しいが、だいたい $O(fib(n))$ となる。
となると、fib(120)の時に$8,670,007,398,507,948,658,051,921$回の関数呼び出しが必要になる。
再帰呼出しが1ナノ秒(10億分の1秒)で行われたとしても、fib(120)の計算には274,924,131年かかることになる。
と本に書いてある。まぁ、とにかく途方にくれる数字とのことです。
それをなんとかしようというのが、動的計画法です。
動的計画法の基本の考え方
例えば、fib(3)が3回呼び出されているように、一度計算した結果を記憶しておけば、何回も何回も計算しなくても済むでは?
というのが、動的計画法の基本の考え方です。とてもシンプルですね。
動的計画法の実装には2つのアプローチがある。
メモ化(memoization)
もとの問題をトップダウンで解きます。元の問題から始まり、部分問題を解いていく、とくたびにその解を記憶しておき、同じ部分問題が再び現れたときには、記憶しておいた解を返す。
表形式(tabular)
もとの問題をボトムアップで解きます。最小の問題から始まり、部分問題を解いていく、とくたびにその解を表に記録していく。最小問題の解答の組み合わせから、より大きな問題の解答を導き出す。
DPでフィボナッチ数列を解く
メモ化
直接コードを見ていきましょう。
def fib_memo(n, memo = None):
"""Assumes n is an int >= 0, memo used only by recursive calls
Returns Fibonacci of n"""
if memo == None:
memo = {}
if n == 0 or n == 1:
return 1
try:
return memo[n]
except KeyError:
result = fib_memo(n-1, memo) + fib_memo(n-2, memo)
memo[n] = result
return result
至ってシンプルですね。memoという辞書を用意して、計算した結果を記憶しておくだけです。
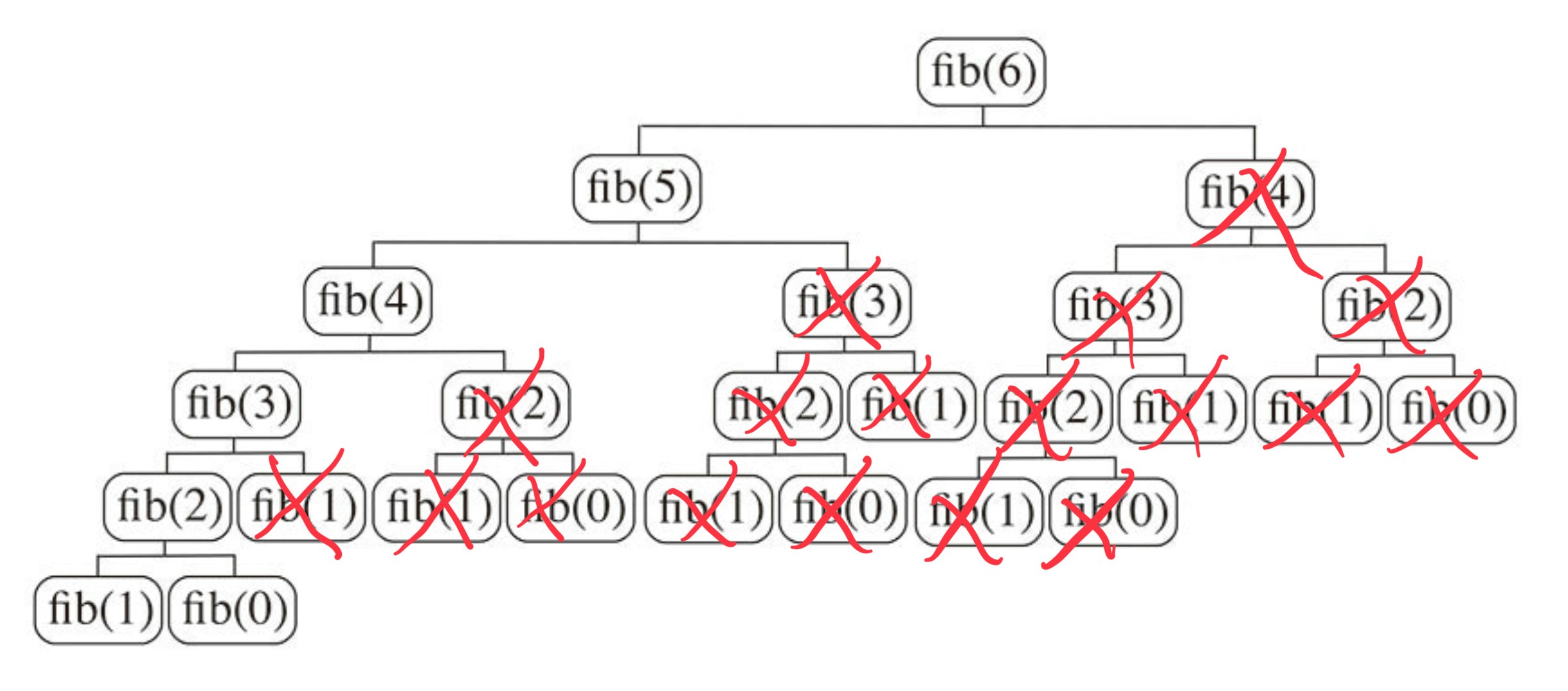
この例でもう一度、fib(6)を実行するときの関数呼び出しのツリーを見てみよう。
かなりの数の関数呼び出しが省略できていますね。
再帰と比べ、DPの計算量は $O(fib(n)) \rightarrow O(n)$ となる。
表形式
次は表形式で実装してみましょう。
def fib_tab(n):
"""Assumes n is an int >= 0
Returns Fibonacci of n"""
tab = [1]*(n+1) #only first two values matter
for i in range(2, n + 1):
tab[i] = tab[i-1] + tab[i-2]
return tab[n]
さらにシンプルになりましたね。計算量は同じく $O(n)$ です。
0/1ナップサック問題の例
問題の解析
さて、腕ならしにフィボナッチ数列の問題を解いてみましたが、ここからが本題です。
0/1ナップサック問題の例を見ていきましょう。
この問題も部分構造の最適性と部分問題の重複性の両方を持つ。
最初、簡単に0/1ナップサック問題を説明してみると、
$n$ 種類の品物(各々、価値 $v_i$、重量 $w_i$)が与えられたとき、重量の合計が $W$ を超えない範囲で品物のいくつかをナップサックに入れて、その入れた品物の価値の合計を最大化するには入れる品物の組み合わせをどのように選べばよいか。(Wikipediaより)
という問題です。
一般的なとき方でいうとして、
貪欲アルゴリズム
容量がいっぱいになるまで、コスパ($\frac{v_i}{w_i}$)が最大のものを入れる。
一度ものをコスパ順にソートするので、計算量は $O(n\log n)$ となる。
総当たり
品物の全ての組み合わせを試してみる。品物集合のすべての部分集合を列挙し、べき集合を総当たりして、容量を超えない価値が最大な組み合わせを探す。
べき集合の数は $2^n$ なので、計算量は少なくとも $O(2^n)$ となる。
解析して、部分構造の最適性と部分問題の重複性を探すにあたり、フィボナッチ数例問題みたいに、解決に至るまでのツリーを書きたいですね。
問題可視化
では、以下の表の品物の価値と重さの例で図を書いてみたいを思います。
| 品物 | 価値 | 重さ |
|---|---|---|
| a | 6 | 3 |
| b | 7 | 3 |
| c | 8 | 2 |
| d | 9 | 5 |
まずは、問題の部分的な解を示し、識別するための4つのラベルを定義します。
- 入れた品:入れると決められた品物の集合
- 残りの品:入れるかどうかまだ決められていない考慮中の品物のリスト
- 現在の総価値:入れると決められた品物の総価値
- 残りキャパ:ナップサックにどのくらいの余裕があるか
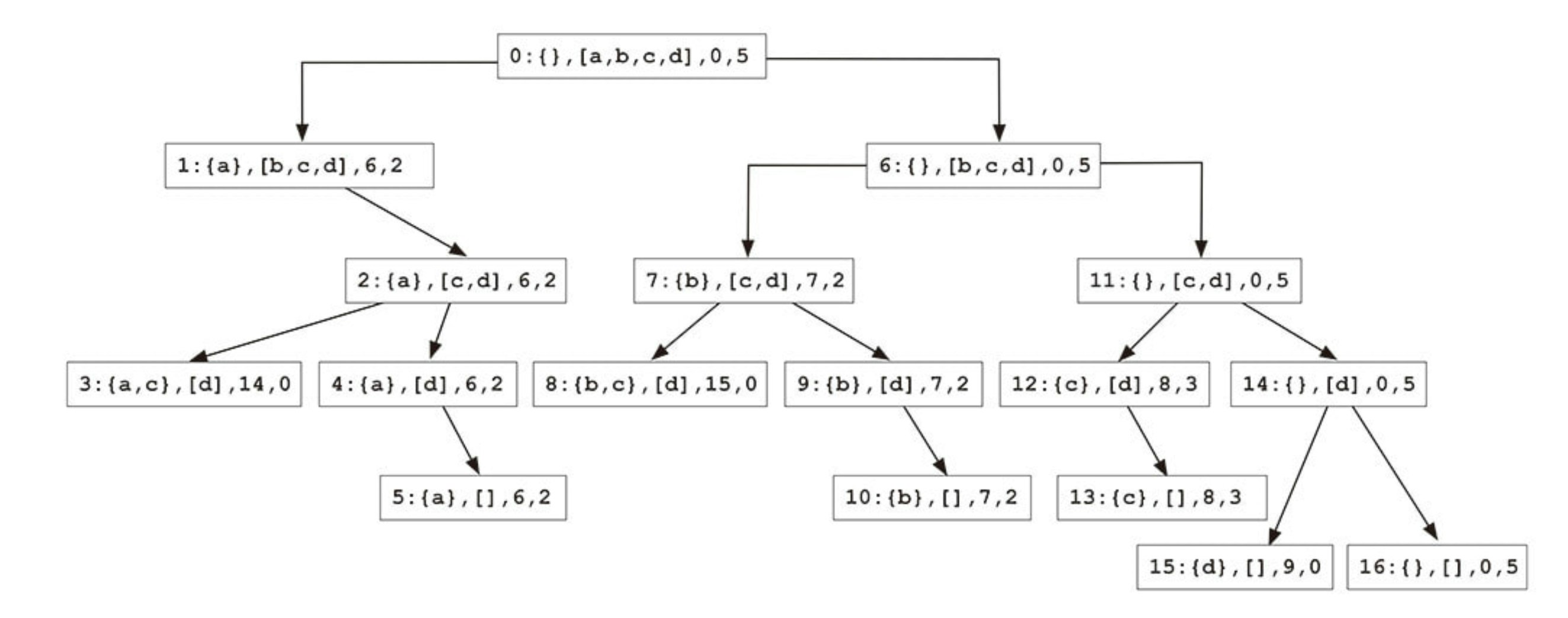
それぞれ、生成された順番:{入れた品},[残りの品],現在の総価値,残りキャパという形で表現します。例えば、初期ナップサックのキャパを5にした時の初期状態が<0:{},[a,b,c,d],0,5>になります。
図を生成する順番を説明する前に、まずは結果を見せよう。
これが生成した決定木図です。
決定木図を生成する順番は要するに品を先頭から一個つづ取り出して、ナップサックに入れるしなの組み合わせをしらみ潰しにさがして行きます。
順番は以下の通りです。生成する順番は左優先、深さ優先です。
- 残りの品の先頭を取り出し、残りキャパが足りるかどうかを判断する
- 足りる -> 入れると決定、ステップ2へ、左のノードを生成する
- 足りない -> 入れないと決定、ステップ3へ、右のノードを生成する
- 残りの品が空 or 容量がいっぱい -> ステップ4へ
- 品を入れて、左のノードを生成する -> ステップ1へ
- 品捨てて、右のノードを生成する -> ステップ1へ
- 親ノードを遡って、右ノードがない親を見つけ、ステップ3へ
この決定木図で0/1ナップサック問題は部分構造の最適性を持つことがわかります。ちょっとややこしいですが、各ノードの解は自分の左と右のノードの解を比べた時、より価値の高いものになります。
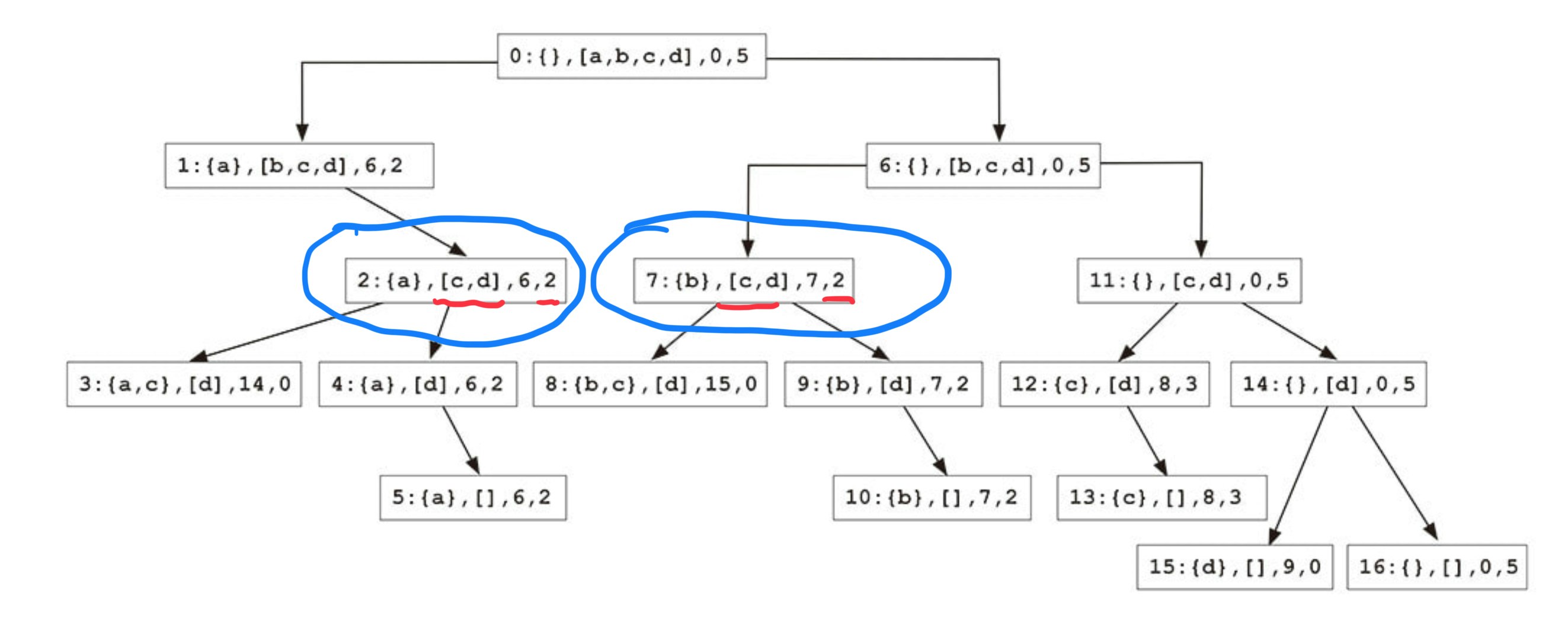
同じノードはありますか?
この質問を答えるには、まず何を持って同じノードとするかを定義する必要があります。
実際に総当たりをしていく中で、次のノードを生成していく時に、何を入れたか(入れた品)とその現在の総価値について考える必要はない。僕らは常に、あとどれぐらい入るか(残りキャパ)、残り何があるのか(残りの品)に注目しています。
これを着目すると、残りキャパと残りの品が一緒なノードを同じノードとしてみることができます。
この定義だと、例の中では、2と7が同じノードになります。
これで、0/1ナップサック問題は部分問題の重複性を持つことがわかります。
DPで0/1ナップサック問題を解く
今回はメモ化のやり方だけで説明します。(本の中もメモ化のやり方だけで説明している)
やり方としては、残りキャパと残りの品をkeyに結果を記憶しておいて、深さ優先探索DFSで決定木を探索していけばいいです。
実装のこちら、説明は割愛します。
class Item(object):
def __init__(self, n: str, v: float, w: float):
self.name = n
self.value = v
self.weight = w
def get_name(self):
return self.name
def get_value(self):
return self.value
def get_weight(self):
return self.weight
def __str__(self):
result = (
"<"
+ self.name
+ ", "
+ str(self.value)
+ ", "
+ str(self.weight)
+ ">"
)
return result
def fast_max_val(to_consider: list[Item], avail: float, memo: dict = {}):
"""Assumes to_consider a list of items, avail a weight
memo supplied by recursive calls
Returns a tuple of the total value of a solution to the
0/1 knapsack problem and the items of that solution"""
if (len(to_consider), avail) in memo:
result = memo[(len(to_consider), avail)]
elif to_consider == [] or avail == 0:
result = (0, ())
elif to_consider[0].get_weight() > avail:
# Explore right branch only
result = fast_max_val(to_consider[1:], avail, memo)
else:
next_item = to_consider[0]
# Explore left branch
with_val, with_to_take = fast_max_val(
to_consider[1:], avail - next_item.get_weight(), memo
)
with_val += next_item.get_value()
# Explore right branch
without_val, without_to_take = fast_max_val(
to_consider[1:], avail, memo
)
# Choose better branch
if with_val > without_val:
result = (with_val, with_to_take + (next_item,))
else:
result = (without_val, without_to_take)
memo[(len(to_consider), avail)] = result
return result
テストのためのコード
def small_test():
names = ["a", "b", "c", "d"]
vals = [6, 7, 8, 9]
weights = [3, 3, 2, 5]
Items = []
for i in range(len(vals)):
Items.append(Item(names[i], vals[i], weights[i]))
val, taken = fast_max_val(Items, 5)
for item in taken:
print(item)
print("Total value of items taken =", val)
def build_many_items(num_items, max_val, max_weight):
import random # not a good idea but ok for now
items = []
for i in range(num_items):
items.append(
Item(
str(i),
random.randint(1, max_val),
random.randint(1, max_weight),
)
)
return items
def big_test(num_items, avail_weight):
items = build_many_items(num_items, 10, 10)
val, taken = fast_max_val(items, avail_weight)
print("Items Taken")
for item in taken:
print(item)
print("Total value of items taken =", val)
これで、以下のように実行すると、結果が出力されます。
small_test()
big_test(10, 40)
big_test(40, 100)
計算量について考える
まずは、メモ化しない時の計算量は前でも言ったように、$O(2^n)$ になります。
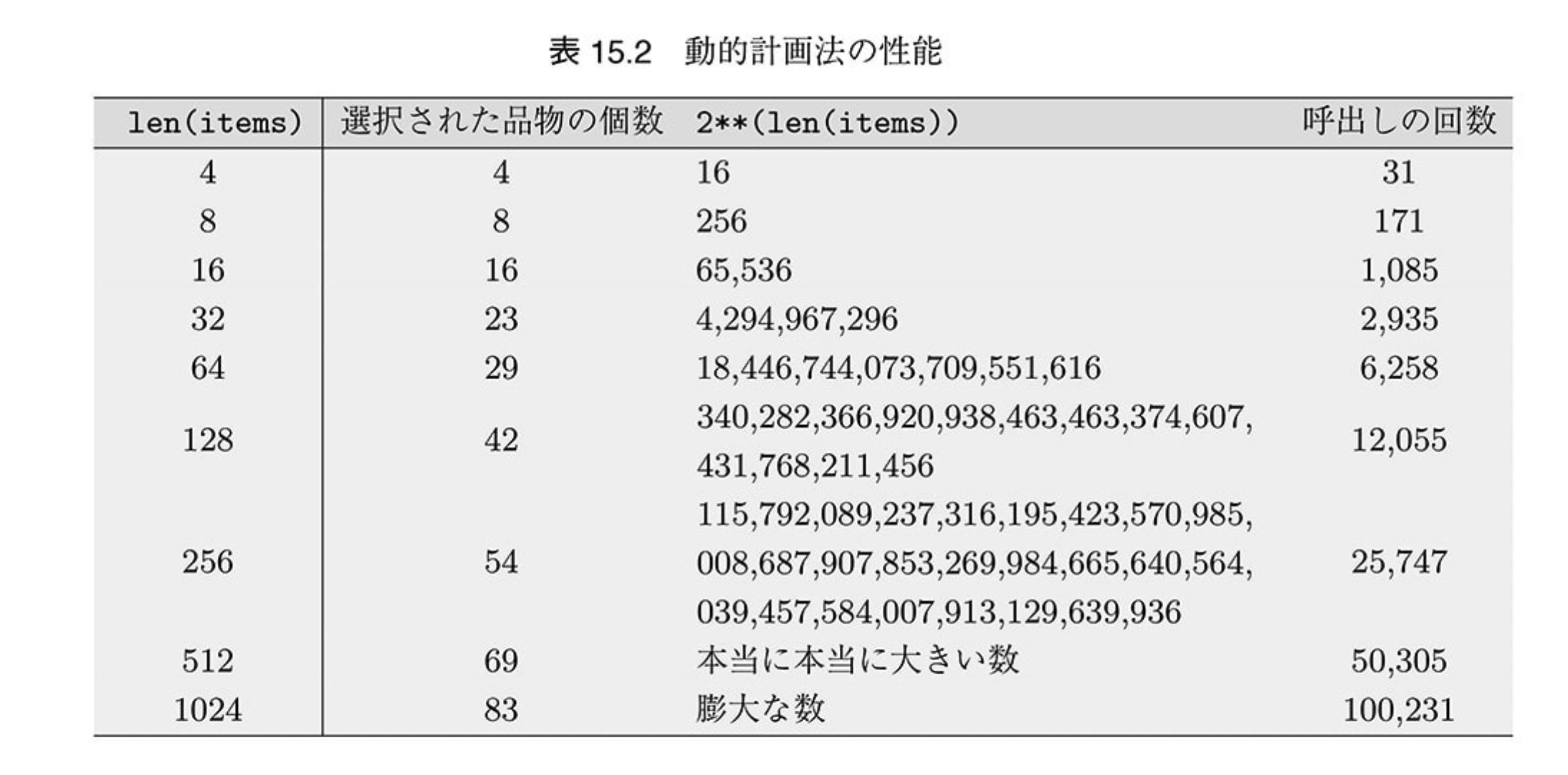
メモ化するときの計算量を実際に測ってみます。
ナップサックのキャパを100とし、品物の数を $2^2$ から $2^{10}$ まで増やしていくとき、上記の実装で計算量を測ってみた結果を以下に示します。
増加の傾向を計算するのは難しいが、あら不思議、$O(n^2)$ よりは遥かに小さいことがわかる。
fast_max_valの計算量を考えていくと、生成される、残りキャパと残りの品の組み合わせが大事になってくる。
品物は先頭から順番に取り出すので、残りの品の最大値は全品物の数のlen(items)になります。
残りキャパのとりうる値を考えるのは難しいが、雑ですが、ナップサックに入れる品物の組み合わせの数以下であることがわかります。
ナップサックに入れる品物を $m$ とすると、その組み合わせの数、べき集合の数は $2^m$ になります。
全品物の数のlen(items)は $n$ とすると、$m \leq n$ なので、$2^m \leq 2^n$ となります。
多少少なくはなりが、理屈ではそれでも大きい数です。
ですが、実際には、品物集合の多くはその総重量が等しいであり、残りキャパの種類が小さいので、計算量あまり大きくならないのですよ。
と本の中では説明されています。
また、これを詳しく調べるには複雑すぎるから、紹介省くよ〜とも書いてあります。
しかし実際はそれほど大きくならないのである。たとえナップサックが大きな容量でも、取りうる品物の総重量の種類がそれなりに小さければ、品物集合の多くはその総重量が等しくなるため、実行時間は著しく削減される。
このアルゴリズムは擬似多項式(pseudo-polynomial)と呼ばれる複雑さのクラスに属する。この概念を詳しく説明することは本書の範囲を越える。大雑把に言うと fast_max_valはavailの取りうる値を表現するのに必要なビット数の指数オーダーの手法である。
さらに、0/1ナップサック問題は、入れる品物の重量を暗黙的に整数に限定されること場合が、なぜか多い。
この制限を考えると、全品物の数のlen(items)を $n$ 、ナップサックのキャパを $c$ とすると
整数の組み合わせの総和は整数しかなれないので、残りキャパの最大種類は $c$
残りの品の最大値は $n$ 、なので、計算量は $O(nc)$ になる。
じゃ品物の重量を整数に限定されない場合は通用しないのか?答えはyesです。
はい、その場合は、残りキャパの種類は非常に多くなり、計算ができなくなります。
上のbuild_many_itemsのコードを以下のように変更して、品物の重量を整数に限定しないすることで、計算量を測ることができます。
def build_many_items(num_items, max_val, max_weight):
import random # not a good idea but ok for now
items = []
for i in range(num_items):
items.append(
Item(
str(i),
random.randint(1, max_val),
- random.randint(1, max_weight),
+ random.randint(1, max_weight) * random.random(),
)
)
return items
本の中で測ってないですが、実際に測ってみると、ナップサックのキャパを100とし
- 品物の数: 4 -> 呼び出し回数: 31
- 品物の数: 8 -> 呼び出し回数: 481
- 品物の数: 16 -> 呼び出し回数: 130561
- 品物の数: 32 -> 計算不可(31840895回で僕が諦めた)
本では
動的計画法は世界共通の認識として奇跡的な技術ではあるが、宗教的な奇跡を成し遂げるわけではない。
と締めぐられています。
最後に
セイちゃんからのDPについての記事でした。
いかがでしたでしょうか?
途中から、あれ?これ著作権的に大丈夫かな?と思い始めたが
まぁ、いいかって、とりあえず書いてみました。
日付が変わる前に間にアップできてよかったです。
一回marpでスライドを作った内容なら、すぐ記事にできると思っていたが、結構時間がかかった。
サボりたかったが、失敗しましたね。
サボリ上手な人になりたいですね。
ではでは
参考文献
本
John V. Guttag(2023)『世界標準MIT教科書 Python言語によるプログラミングイントロダクション 第3版』 (久保 幹雄監訳, 麻生 敏正ほか訳) 近代科学社
ソースコード