LoginSignup
13
15

More than 1 year has passed since last update.

@Kuno3

LightweightMMMのモデルの解説

Last updated at Posted at 2023-03-21

1.Marketing Mix Modeling(MMM)とは

  • MMMとは，複数の広告への投資がそれぞれKPIにどの程度影響するかを推定し，投資配分を最適化するための手法を指す．
    • 例：アプリ広告・Web広告・雑誌広告がそれぞれ売上にどれぐらい影響するかを調べる．
  • 歴史のある手法だが，各広告への支出とKPIのデータだけあればよく，個人情報を利用しないため，クッキーレスの流れに伴い近年注目されている．
  • 様々なベンダーがサービスを提供しているのに加え，GoogleのLightweightMMM，MetaのRobyn，UberのOrbitなど，近年ビッグテック企業が相次いでパッケージを公開している．
  • 手法としては，近年はベイジアン非線形時系列モデルが用いられることが多い．

2 LightweightMMM(Google)について

2.1 LightweightMMMとは

2.2 LightweightMMMのモデル

LightweightMMMでは，KPIを出力とし，投資額やその他の特徴量を入力として，以下のようにKPIをモデル化する．

KPI = 定数 + トレンド + 季節性 + 投資効果 + その他の特徴量

モデルの各項について説明する．

  • KPI

    • 概要：売上やCVなどが入る．正の値をとることが想定されている．

  • 定数項（$intercept$）

    • 概要：普通の定数項で，正の値をとることが想定されている．
    • モデル：$intercept = a$
    • デフォルトの事前分布：
      • $a \sim HalfNormal(2)$

  • トレンド項（$trend_t$）

    • 概要：単純だが，非線形なトレンドを捉えることができる項である．
    • モデル：$trend_t = \mu t^\kappa$
    • 詳細：
      • $\mu$はトレンド項の係数．
      • $\kappa$は$0.5$から$1.5$の値をとる．$1$より小さい場合，時間がたつにつれ変化の幅がサチる．1より大きい場合，時間がたつにつれ変化の幅が増加していく．
    • デフォルトの事前分布：
      • $\mu \sim Normal(0, 1)$
      • $\kappa\sim Uniform(0.5, 1.5)$

  • 季節項（$seasonality_t$）

    • 概要：逆フーリエ変換のような発想で，週ごとのデータを用いる場合は52週，日毎のデータを用いる場合は365日の周期の三角関数の和で季節性をモデル化する．
    • 週ごとのデータを用いる場合
      • モデル：$seasonality_t=\sum_{d=1}^2\left(\gamma_{1, d} \cos \left(\frac{2 \pi d t}{52}\right)+\gamma_{2, d} \sin \left(\frac{2 \pi d t}{52}\right)\right)$
      • デフォルトの事前分布：
        • $\gamma_{1, d}, \gamma_{2, d} \sim \operatorname{Normal}(0,1)$
    • 日ごとのデータを用いる場合
      • モデル：$seasonality_t=\sum_{d=1}^2\left(\gamma_{1, d} \cos \left(\frac{2 \pi d t}{365}\right)+\gamma_{2, d} \sin \left(\frac{2 \pi d t}{365}\right)\right) + \delta_{t (mod 7)}$
      • デフォルトの事前分布：
        • $\gamma_{1, d}, \gamma_{2, d} \sim \operatorname{Normal}(0,1)$
        • $\delta_t \sim \operatorname{Normal}(0,0.5)$

  • 投資効果（$media \ channels_t$）
    この項が最も特徴的で，特に投資効果の累積の仕方とサチり方のモデル化に特徴がある．Carryoverモデル，Adstockモデル，Hill_adstockモデルの3種類のモデルを利用できる．これら3種類のモデルについて説明する．

    • Carryoverモデル

      • 概要：$L$期分の投資額を重み付け平均し，$\rho_m$乗して，係数を掛けるモデル．
      • モデル：
        • $media \ channels_t = \beta_m x_{t, m}'^{\rho_m}$（おそらく公式ドキュメントは誤っている）
        • $x_{t, m}'=\frac{\sum_{l=0}^L \tau_m^{\left(l-\theta_m\right)^2} x_{t-l, m}}{\sum_{l=0}^L \tau_m^{\left(l-\theta_m\right)^2}}$ where $L=12$
      • 詳細：
        • $x_{t, m}$は$t$時点のメディア$m$に対する投資額やインプレッションを用いる．
        • $\rho_m$が0から1の値をとるので，累積投資額$x_{t, m}'$の影響はサチる
        • $x_{t, m}'$は$x_{t, m}$を$\tau_m^{\left(l-\theta_m\right)^2}$で重みづけた$L$期分の重み付け平均で，$\tau_m$が0から1の値をとるので，$l$が$\theta_m$から離れるほど投資の効果が小さくなる．
        • $\theta_m$は何期前の重みが最も大きくなるかを決める．例えば，$\theta_m=5$なら5期前の投資の効果が最も大きくなる．
        • 横軸が$l$（ラグ）で縦軸が$\tau_m^{\left(l-\theta_m\right)^2}$（重み）のグラフ（黒線が$\tau_m=0.8, \theta_m=0$，赤線が$\tau_m=0.8, \theta_m=5$）
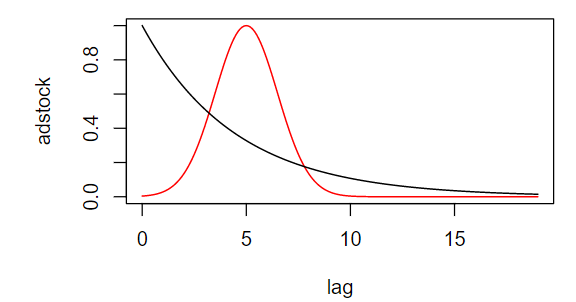
          lag_adstock.png
      • デフォルトの事前分布
        • $\tau_m \sim \operatorname{Beta}(1,1)$
        • $\theta_m \sim HalfNormal(2)$
        • $\rho_m \sim \operatorname{Beta}(9,1)$
        • $\beta_m \sim HalfNormal(v_m)$（$v_m$はコストのトータル）

    • Adstockモデル

      • 概要：ほとんど単なる自己回帰モデル．
      • モデル：
        • $media \ channels_t=\beta_m x_{t, m, s}'^{\rho_m}$（おそらく公式ドキュメントは誤っている）
        • $x_{t, m, s}'=\frac{x_{t, m}'}{1 /\left(1-\lambda_m\right)}$
        • $x_{t, m}'=x_{t, m}+\lambda_m x_{t-1, m}'$ where $t=2, \ldots, N$
        • $x_{1, m}'=x_{1, m}$
      • 詳細：
        • $x_{t, m}$は$t$時点のメディア$m$に対する投資額やインプレッションを用いる．
        • $\rho_m$が0から1の値をとるので，累積投資額$x_{t, m, s}'$の影響はサチる．
        • $1+\lambda_m+\lambda_m^2+\cdots = 1/(1-\lambda_m)$なので，$x_{t, m}'$を$1/(1-\lambda_m)$で割っている（おそらく）．
      • デフォルトの事前分布
        • $\lambda_m \sim \operatorname{Beta}(2,1)$
        • $\rho_m \sim \operatorname{Beta}(9,1)$
        • $\beta_m \sim HalfNormal(v_m)$（$v_m$はコストのトータル）

    • Hill_adstockモデル

      • 概要：投資効果のサチり方をHill関数という関数によりモデル化．投資額の累積の仕方は自己回帰モデル．
      • モデル：

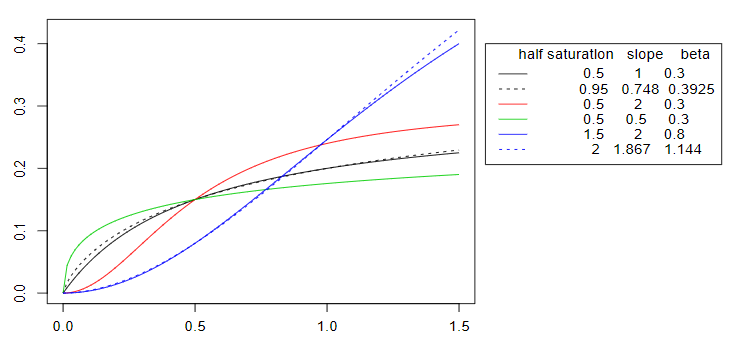
        • $media \ channels_t= \frac{\beta_m}{1+\left(x_{t, m}' / K_m\right)^{-S_m}}$（これがHill関数）

        • $x_{t, m}'=x_{t, m}+\lambda_m x_{t-1, m}'$ where $t=2, \ldots, N$

        • $x_{1, m}'=x_{1, m}$

      • 詳細：
        • $x_{t, m}$は$t$時点のメディア$m$に対する投資額やインプレッションを用いる．
        • Hill関数の形は次の画像を参照(Half saturationが$K_m$，slopeが$S_m$)
          hill_function.png
      • デフォルトの事前分布
        • $K_m \sim Gamma(1,1)$
        • $S_m \sim Gamma(1,1)$
        • $\lambda_m \sim Beta(2,1)$
        • $\beta_m \sim HalfNormal(v_m)$（$v_m$はコストのトータル）

  • その他の特徴量（$other \ factors_t$）

    • 概要：投資額以外の入れたい特徴量に係数を掛けただけの通常の線形回帰のような項である．
    • モデル：$other \ factors_t = \sum_{i=1}^N \lambda_i Z_i$
    • 詳細：
      • $Z_i$は投資額以外の特徴量（例：プロモーションフラグ）．
    • デフォルトの事前分布
      • $\lambda_i \sim Normal(0,1)$

2.3 利用方法

使い方は公式のExampleのノートブックが分かりやすい．以下で抜粋する．

  • Exampleではシミュレーションデータを扱っている．パッケージにはシミュレーションデータを生成する機能もあり，以下のようなコードで生成できる．
media_data, extra_features, target, costs = utils.simulate_dummy_data(
    data_size=data_size,
    n_media_channels=n_media_channels,
    n_extra_features=n_extra_features)
  • モデルのfitは簡単で，下記のようにscikit learnやLight GBMライクに実行できる
mmm = lightweight_mmm.LightweightMMM(model_name="carryover")
mmm.fit(
    media=media_data_train,
    media_prior=costs,
    target=target_train,
    extra_features=extra_features_train,
    number_warmup=number_warmup,
    number_samples=number_samples,
    seed=SEED)
  • 予測や可視化なども簡単に実行できる
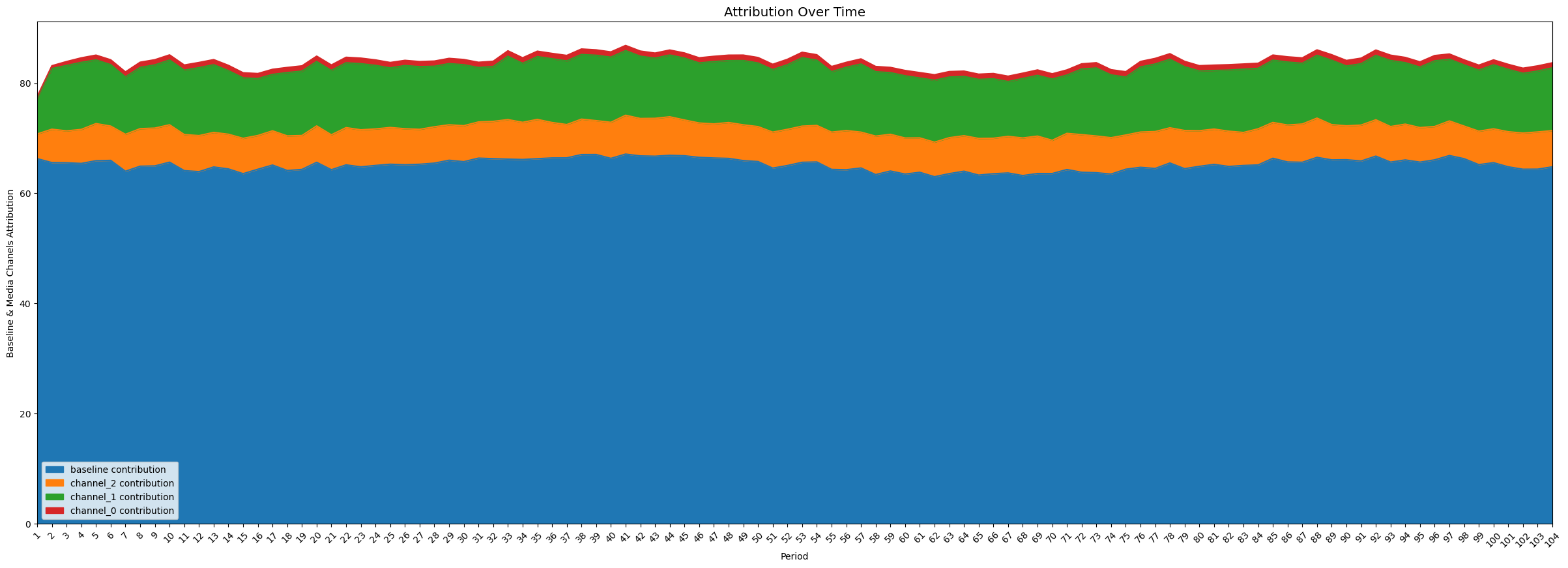
    • 例えば，各メディアがどれだけKPIに寄与しているかを可視化することができる・
plot.plot_media_baseline_contribution_area_plot(media_mix_model=mmm,
                                                target_scaler=target_scaler,
                                                fig_size=(30,10))

attribution_over_time.png

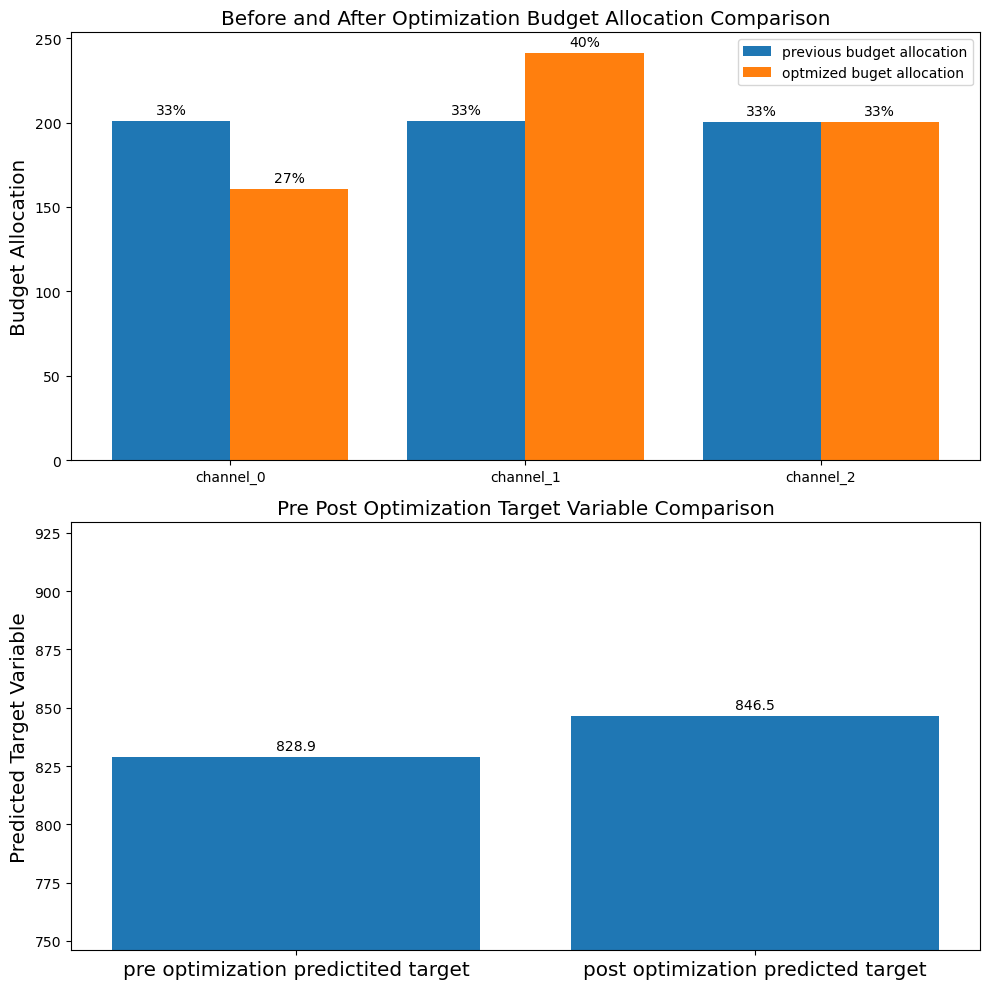
  • また，最適な予算配分を算出することも可能である 
# Plot out pre post optimization budget allocation and predicted target variable comparison.
plot.plot_pre_post_budget_allocation_comparison(media_mix_model=mmm, 
                                                kpi_with_optim=solution['fun'], 
                                                kpi_without_optim=kpi_without_optim,
                                                optimal_buget_allocation=optimal_buget_allocation, 
                                                previous_budget_allocation=previous_budget_allocation, 
                                                figure_size=(10,10))

投資額最適化.png

2.4 元論文での使用例

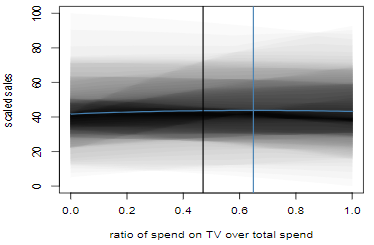
　若干モデルが異なるが，Jin et al. (2017)における適用例も簡単に紹介する．投資額や売上額のスケールが調整されているため直感的な理解には繋がらないが，各メディアへの投資額がどのように売上に貢献するかを分析できていることが分かる．

問題設定

項目 内容
対象 あるシャンプーの広告
メディア テレビ，雑誌，ディスプレイ，YouTube
特徴量 価格，流通量，プロモーション
モデル 4モデルからBICにより選択

推定結果の一部

  • テレビの推定投資効果のHill関数（横軸はTVへのスケール調整後の投資額）
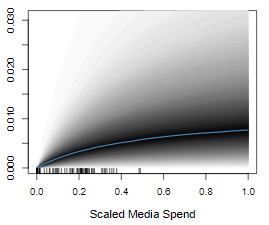
    Hill関数.png

  • 投資額全体に対するテレビへの投資比率と売上の関係

    • 黒と水色の縦線は最適なテレビへの投資比率（ベイズ推定のため，推定値にばらつきがあり，そのばらつきをどう考慮するかで最適な点が2つでてくる）
      TVへの投資と売上の関係.png

3 個人的な感想

  • まだまだ作成されてまもないパッケージのため，ドキュメントが粗く情報が少ない．
  • 実際にこのモデルで投資配分を最適化して売上があがった例を探したが，見つからなかった．
  • 投資額を大きくしたタイミングでその他の要因でKPIも上昇した場合，効果が過大に見積もられるので，因果効果を主張するためには，用いる特徴量について十分に考える必要がありそう．
  • 投資効果の項を除けば基本的にはシンプルな時系列モデル．ただ，トレンド項や季節項のモデリングは少し工夫されていて面白い．
  • stanなどで実装することもそれほど難しくはなさそう．ただ最適化などまで一発で実行できるのは便利．
  • デフォルトの事前分布はかなり経験的に決められており，事前分布に合わせて各変数のscalingを適切に行うには慣れが必要そう．

4 参考

13
15
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
13
15