ベータ分布に従う2つの確率変数の差の分布を数値積分により算出する方法

　ベイジアンABテストなどで、ベータ分布に従う2つの確率変数の差の分布を知りたくなることがあります。しかし、これは解析的には導出できないため、サンプリングにより近似することが多いと思います。ただ、例えば滑らかな確率密度関数を得ようとすると、大量のサンプリングが必要になり使い勝手が悪いです．

　そこで、本ページでは、scipyの数値積分のための関数であるintegrateを使って、ベータ分布に従う2つの確率変数の差の確率密度関数や累積分布関数を計算する方法について記載します．

　以下では、実装方法を記載し、その使い方について記載します．

実装方法

　まず、実装は以下においています．

例えば，確率密度関数を計算する箇所は以下です．

    def pdf(self, t):
        betaln1 = betaln(self.alpha1, self.beta1)
        betaln2 = betaln(self.alpha2, self.beta2)
        if t <= -1 or t >= 1:
            return 0
        elif t <= 0:
            val = integrate.quad(
                beta_diff.jnt_dst,
                -t,
                1,
                args=(t, self.alpha1, self.beta1, self.alpha2, self.beta2, betaln1, betaln2),
            )[0]
            return val
        else:
            val = integrate.quad(
                beta_diff.jnt_dst,
                0,
                1 - t,
                args=(t, self.alpha1, self.beta1, self.alpha2, self.beta2, betaln1, betaln2),
            )[0]
            return val

次に使い方について説明します。使い方はscipy.statsの各種分布のための関数ライクに使うことを想定しています。試しに$Beta(11, 11)$と$Beta(16, 6)$に従う確率変数の差の分布を出してみます．下記のように、まず、2つのベータ分布のパラメータを指定して、その後、確率密度関数や累積分布関数を算出します。平均と分散、標準偏差も一応実装しています。

beta_diff_test = beta_diff(11, 11, 16, 6)
print('差が0となるときの確率密度関数:', beta_diff_test.pdf(0))
print('差が0以下になるときの累積分布関数:', beta_diff_test.cdf(0))
print('平均値:', beta_diff_test.mean())
print('分散:', beta_diff_test.var())
print('標準偏差:', beta_diff_test.std())

差が0となるときの確率密度関数: 0.7659444329930765
差が0以下になるときの累積分布関数: 0.9445509291914406
平均値: -0.2272727272717359
分散: 0.019493352488142934
標準偏差: 0.1396185964982564

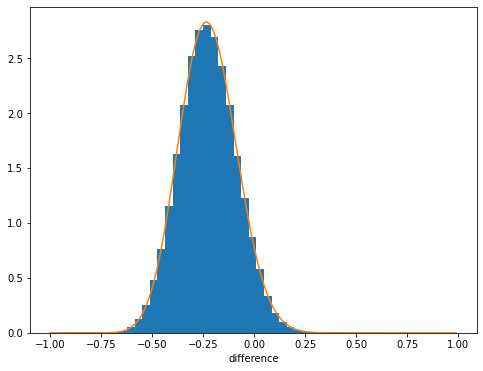
　100000個サンプリングした場合のヒストグラムと比較したものが以下です。精度良く確率密度関数が計算できていることが分かります。

　また、下記のように差が0となる点での確率密度を算出するための実行時間を計測すると、google colaboratory pro上で29 µsとかなり高速であることが分かります。

%timeit beta_diff_test.pdf(0)

29 µs ± 821 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)