はじめに
MATLABのSimulinkで作成した信号処理ロジックについて、周波数特性を評価した。
周波数特性の評価方法は様々な手法がMATLABでは用意されているようだが、今回はSimulink Control DesignツールボックスのModel Linearizerアプリを使用した。
Model Linearizerアプリを使用した理由
Model Linearizerを用いて周波数特性を評価する際は、可変周波数の正弦波を入力し、出力を入力した正弦波の周波数毎に評価することで周波数特性を求めるようであり、伝達関数を求めずに直接的に周波数特性を得られる。このため、自前で作成した任意の信号処理ロジックの妥当性確認に使用できると考えた。
問題となった点
信号処理ロジック内ではサンプリングレートの変換等を行うため、この影響まで評価したかった。そこで、信号処理ロジック内にZero-Order Holdを用いて離散サンプリング化やデシメーションをしていた。Model Linearizerでこれに適切な入力信号をGUIで生成するが、セトリング時間を入力信号の周波数によらず一定にしたかったところ、GUIでは一括指定は周期でしかできなかった。
セトリング時間を入力信号の周波数によらず一定にする方法が分かったため、この手順を含めて以降紹介する。
MATLAB環境
・ノートPC(windows10 64bit)
・MATLAB R2021b 64bit
・MATLABツールボックス:Simulink Control Design(依存するツールボックスを含む)
参考・リンク
本記事の主な情報源
・周波数応答のオフライン推定
・frest.Sinestream
・frest.createFixedTsSinestream
・モデルの一部を線形化するよう指定
・frestimate
System Identification Toolboxを使う方法
・周波数応答プロット
・System Identification Toolbox 入門
Control System Toolboxを使ったシステム応答のプロット方法
・システム応答のプロット
オンラインでの周波数応答の推定方法
・Frequency Response Estimator
手順1-1 サンプル動作確認
基本的には以下に記載の手順に従えば周波数特性が評価できる。
モデル線形化器を使用した周波数応答の推定
このため、まずは上記に従って、サンプルモデルに対して周波数特性の評価をしてみる。
手順2-1 周波数特性解析
下図のように、評価対象とする信号処理ロジックをSimulink上で作成する。この時、Zero-Order Holdによる離散サンプリング化を含むものとする。ただし、周波数解析を行う入力点と出力点のサンプル時間は同じである必要があるため、デシメーションを行った信号について、Zero-Order Holdを用いてサンプル時間を入力と同じになるようにしている。
信号線を右クリックして"Linear Analysis Points"を選び、周波数特性を解析する入力点と出力点を設定する。
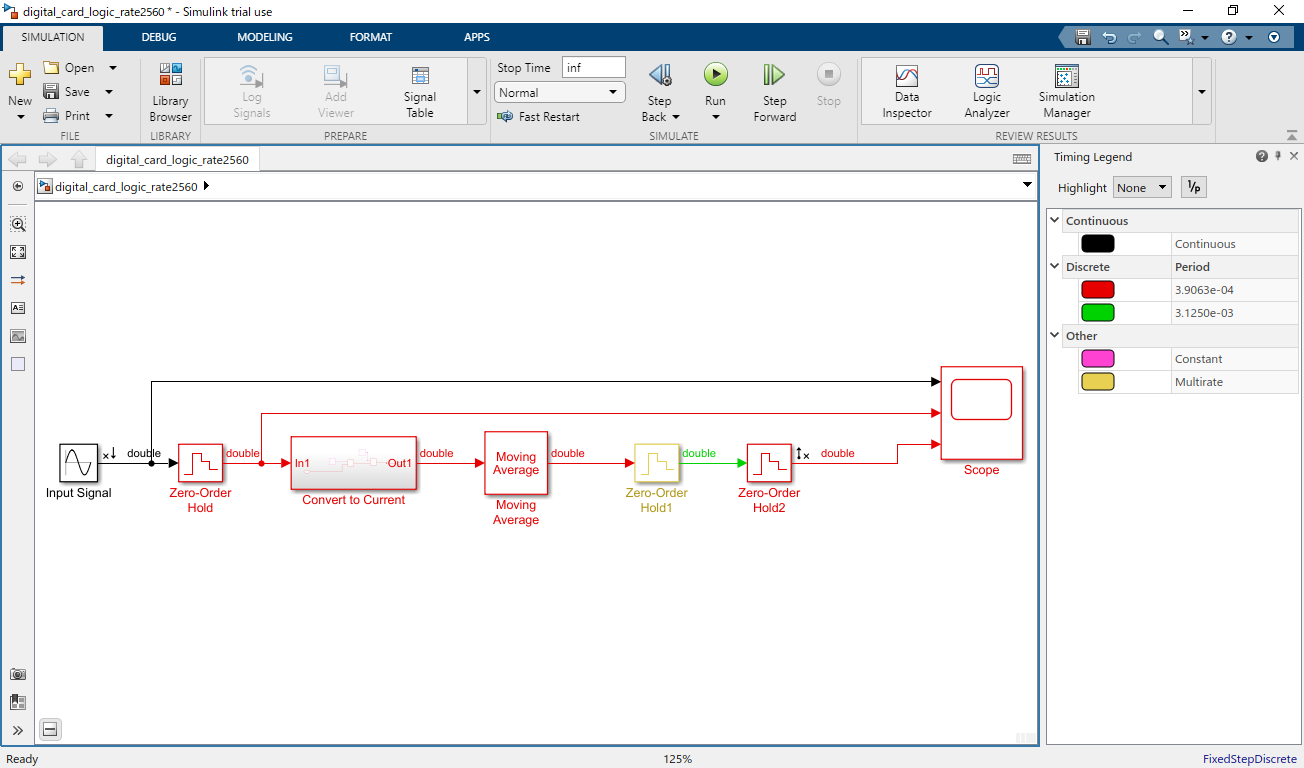
手順2-2
Model Linearizerアプリの提供する手段によって、一旦評価対象の信号処理ロジックの周波数特性を解析できることを確認する。SimulinkのAPPSタブを選択し、"Model Linearizer"をクリックして立ち上げる。

手順2-3
固定サンプル時間に対応した可変周波数の正弦波入力を生成するため、以下を選択する。
ESTIMATIONタブ⇒"Input Signal"の"Create New"⇒"Fixed Sample Time Sinestream..."

手順2-4
サンプル時間(サンプリング周波数の逆数)を適宜入力した後に下図画面が現れる。この画面において、"Create New"⇒"Sinestream"を選んで波形を生成する場合に表示されていた"Number of samples at each period"の表示(Settling periodsの下)がない。これにより、離散サンプリング化した信号処理ロジックに対応した正弦波入力の生成が行えていることを確認できる。
あとは、手順1の方法と同じく、プラスボタンを押して入力する周波数を設定し、"Bode"を押して周波数特性の解析と結果の表示を実行する。
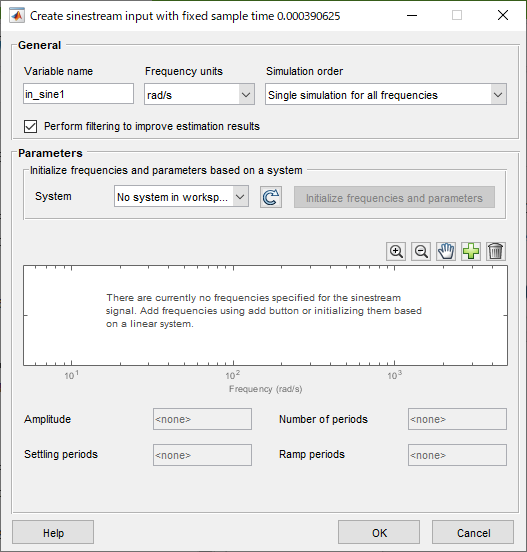
手順3-1 セトリング時間一定
上記手順5まではMATLAB側で用意された通常の手段である。しかし、上記方法だと"Settling periods"を全ての周波数において同じ値に設定することは容易だが、セトリング時間を入力信号の周波数によらず一定にするには、手順5の画面上で全ての点について"Settling periods"を一つずつ手動で入力する必要があり困難である。
そこで、入力信号はMATLAB上で次のコマンドを入力して生成する。
ts = 1/2560; %サンプル時間
ws = 2*pi()/ts; %サンプルレート[rad/s]
sppmax = round(ws); %1周期のサンプル数の最大値
sppmin = 20; %1周期のサンプル数の最小値(3以上)
sppnum = 30; %1周期のサンプル数の数
spp = round(logspace(log10(sppmax),log10(sppmin),sppnum)); %1周期のサンプル数のベクトル
spp = sort(unique(spp),'descend'); %重複した要素を削除
w = ws./spp; %周波数のベクトル
amps = 1; %振幅
settling_time = 1; %定常状態に達するまでの時間
settling_periods = settling_time*ceil(w/2/pi()); %定常状態に達するまでの周期数
input = frest.createFixedTsSinestream(ts,w);
input.Amplitude = amps;
input.NumPeriods = settling_periods+4;
input.SettlingPeriods = settling_periods;
上記により、セトリング時間が一定の可変周波数の正弦波入力であるinputという名前のSinestreamオブジェクトが生成される。上記で生成したSinestreamは、以下のコマンドで作成したSinestreamの振幅を1とし、NumPeriodsとSettlingPeriodsを変更したものに同じにしている。
input = frest.createFixedTsSinestream(1/2560)
input.Amplitude = 1;
frest.createFixedTsSinestream(ts)を使用すると解析できる周波数の点が30点に固定されてしまうため、先に記載した様に周波数ベクトルwを作成した後にfrest.createFixedTsSinestream(ts,w)によって正弦波入力を生成する方法を取った。これにより、解析する周波数や点数を自由に変更できるようになる。特に注意する点は、frest.createFixedTsSinestreamの仕様上、上記コードにおける変数"spp(SamplesPerPeriod)"は1以上の整数になるようにする必要がある。sppを整数で設定した後に周波数w(こちらは実数でよい)を計算することがポイントとなる。
手順3-2
Model LinearizerでInput Signalをクリックすると、"input"が選択できるので、これを入力信号として指定する。あとは通常通り"Bode"を押して周波数特性の解析と結果の表示を実行する。下図は入力信号としてinputを選んだ状態で実際に"Bode"を実行した後の画面の様子を示す。
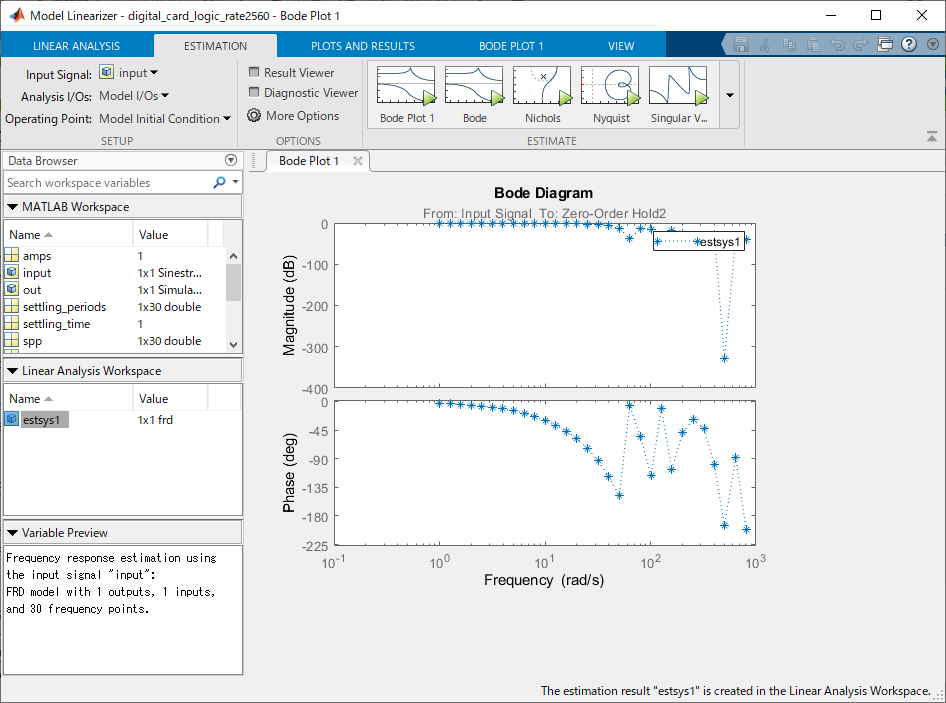
以上、参考になれば幸いです。