LoginSignup
24
19

More than 3 years have passed since last update.

@Kuma_T

このゲーム（積立投資）には必勝法がある　－持株会ゲーム－

Last updated at Posted at 2018-12-17

秋山深一「このゲームには必勝法がある」
神崎直「どういうことですか！秋山さん！」

（こんな記事を開いちゃった）なおちゃんってほんと ばかだよねえええ！！！

懐かしいですね、ライアーゲームのドラマ。
面白かったです。オススメです。

1. 持株会の効果を最大化したい

そこそこの規模の会社には、従業員持株会という制度があると思います。
毎月、一定額を支払って株式を購入できるという制度です。(積立投資)

会社の財務状況を調べてみたら潰れる心配もなさそうで、辞める気もそんなになく、
金銭的な余裕もでてきたので持株会で投資でも始めようかなと思いました。

持株会の最大のメリットは、奨励金が出て、配当金が再投資され、少額からも株を買えることかなと思います。1
調べたところ、奨励金は5-10%くらいが一般的だそう。
インカムゲインである配当金もそのまま再投資されます。
また、月1,000円からでも少しずつ積み立てていけるのは（このあとの話の展開的に）おいしいです。

額が大きくなったら、複利で配当金ウハウハになるんじゃないかと思い、
「持株会」というルールの中で最大化する方法を真面目に計算してみようと思いました。

もちろん、会社に入っていない人や持株会のない人も、
通常の投資信託とほぼ変わりないので、頭の中で置き換えて読んでいただければと思います。

2. ドルコスト平均法は調和平均だ

持株会では一般的に一定金額を毎月積み立てるので、定額購入になります。
価格が安いときは多く、価格が高いときに少なく買うため、
定量購入よりも平均取得単価が安くなる（同じ投資額で多くの株が購入できる）ことが知られています。

これがドルコスト平均法です。
以下のように、価格が800-1200円、10口前後で購入する場合を簡単にシミュレーションします。

1回目 2回目 合計投資額 平均購入金額
価格 800円 1,200円
定量購入 8,000円 12,000円 20,000円 1,000円
10口 10口 20口
定額購入 10,000円 10,000円 20,000円 962円
12.5口 8.3口 20.8口

以上のように、同じ20,000円を投入しても、定額購入（ドルコスト平均法）の方がお得だとわかります。

これは、数学的に表すと、定量購入(相加平均) ≧ 定額購入(調和平均) ということになります。
リンク：調和平均にまつわる重要な公式まとめ

調和平均について、Wikipedia先生のお言葉を引用しておきます。

例えば速度の平均を計算することを考えると、乗り物がある距離を時速 60 km で走りそれから同じ距離を時速 40 km で走った場合、全体の走行時間と走行距離から求められる平均速度は調和平均の値である時速 48 kmであって、算術平均によって求められる時速 50 km を平均とするのは適切ではない。

この文章の数値で特徴的な点は、調和平均は、時速 40 km という小さい方の数字に引っ張られるということです。
これのおかげで、相加平均以下になるんですね。

このように、持株会では定額購入により、価格が安いときは多く、価格が高いときに少なく買うためお得になることがわかりました。

逆に売るときは、高い時の口数を増やしたいので、定額売却よりも定数売却の方がお得です。
（一部では逆ドルコスト平均法とも呼ばれている）

もちろん、売るときは一括で全て売却もできます。まとまったお金がほしいなどの理由で、一括で売るときもあると思います。

複利で配当金ウハウハ狙いじゃないならば、株初心者にはいつ売ればいいかもわからないので、
上げ下げで一喜一憂するくらいなら、100株溜まったら売るくらいが効率が良さそうです。

結論１：定額で積み立てられるドルコスト平均法はそれなりにお得

3. ドルコスト平均法は確実に儲かる手法ではない

持株会は、ドルコスト平均法で買うようなシステムになっているので「なんとなく」お得だということはわかりました。

ドルコスト平均法でお金が増えるのかどうか、シミュレーションしてみます。
市場の本質はランダムウォーク、
乱数を発生させた株価を模擬し、10000回で何回儲かるかを計算します。

以下が、模擬した株価の一例です。この例の場合は、終値/平均取得金額 = 1.0倍なので、儲けも損もないです。
0.png

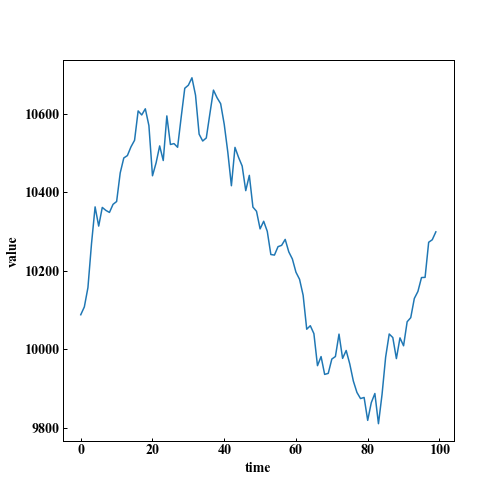
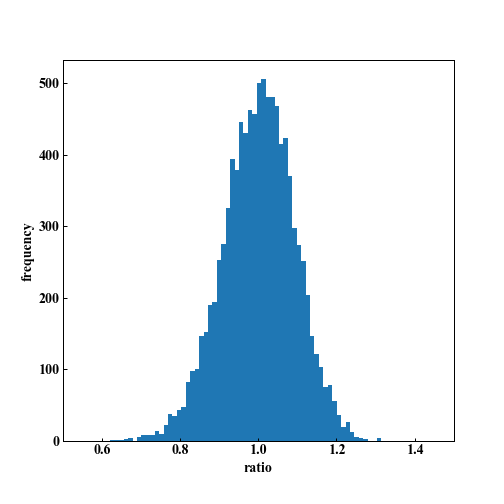
以下、L回ドルコスト平均法で株を購入し、最後に買った瞬間に売った場合に儲かるかを調べています。
1倍以上になったら儲かっています。

コード1
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader.data as web
from datetime import datetime

plt.rcParams['figure.figsize'] = [5, 5]
plt.rcParams['xtick.direction'] = 'in' #x軸の目盛線が内向き('in')か外向き('out')か双方向か('inout')
plt.rcParams['ytick.direction'] = 'in' #y軸の目盛線が内向き('in')か外向き('out')か双方向か('inout')
plt.rcParams['xtick.major.width'] = 1.0 #x軸主目盛り線の線幅
plt.rcParams['ytick.major.width'] = 1.0 #y軸主目盛り線の線幅
plt.rcParams['font.size'] = 12 #フォントの大きさ
plt.rcParams['axes.linewidth'] = 1.0 # 軸の線幅edge linewidth。囲みの太さ
plt.rcParams['font.family'] =  'Times New Roman' #使用するフォント名
コード2(ドルコスト平均法)
L=100 #購入回数
a = np.array([])

for i in range(10000):
    np.random.seed(i) #np.random のシード値を決定
    value = 50*np.cumsum(np.random.randn(L))+10000 #株価を模擬
    ratio = value[L-1]/stats.hmean(value) #終値/平均取得金額
    a = np.append(a, ratio)

b= a>1
print("1以上になった数は "+str(np.sum(b))+"回") #1以上の回数を出力

plt.hist(a, bins='auto')
plt.xlim(0.8, 1.2)
plt.xlabel("ratio")
plt.ylabel("frequency")
#plt.savefig('%d.png' %L)
plt.show()

1000.png
「1以上になった数は 5062/10000回」

この結果を見るに、ドルコスト平均法で買ったからといって儲かるわけではないことがわかります。

結果から、いくつかのパターンを抜き出してみましょう。

めちゃ儲かるパターン

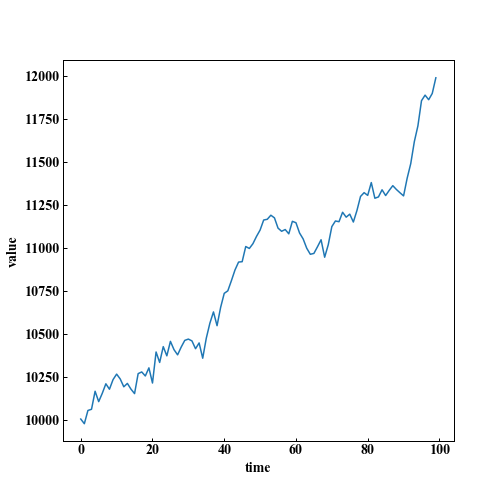
820.png
1.10倍になりました。
当然のような話ですが、株価が上がり続ける限りは儲かることがわかります。

意外と儲かってたパターン

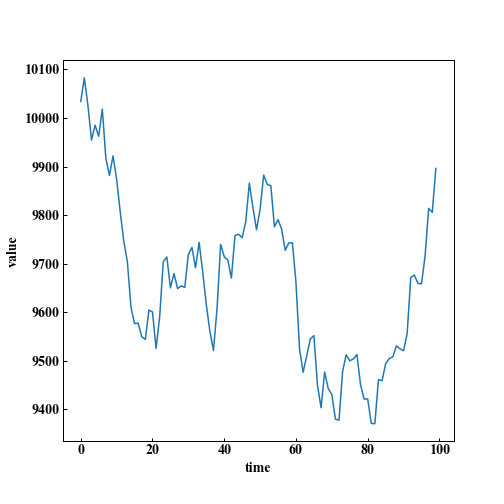
1207.png
1.02倍になりました。
スタートの10,000円付近よりは下がっていましたが、
ドルコスト平均法で取得単価を下げ、最後に帳尻を合わせたように株価が上がったため増えてたパターンです。

とても損したパターン

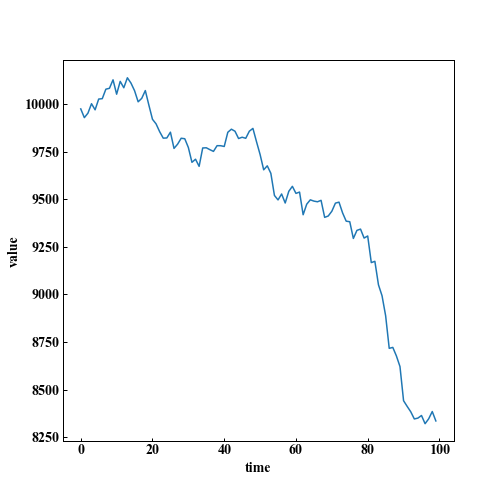
3433.png
0.88倍になりました。
ずっと下げていましたが、最後に大暴落していました。
これじゃあ儲からないですよね。

結論２：ドルコスト平均法を使っても、株数が増えるだけで、儲かるわけではない

4. 経済成長バンザイ

儲かってたパターンを見て明らかなように、何かしら株価の上昇の傾向がないと資金は増えはしないです。
じゃあ株価の上昇がある場合はどうだろう。
当然ですが、お金を稼ぐために仕事をしているわけで、それに伴って経済は成長しているはずです。

高度経済成長とはいかないですが、近年は平均1%/年で成長しているみたいです。
リンク：経済成長率の推移

以下、1%の経済成長（株価の上昇）を仮定して計算してみます。
（株価はもっと上げ下げが大きいですが、シミュレーションということで）

コード3(経済成長)
L=100 #購入回数
g = 0.01 #経済成長率
a = np.array([])

for i in range(10000):
    np.random.seed(i) #np.random のシード値を決定
    value = (50*np.cumsum(np.random.randn(L))+10000) #株価を模擬
    value = value*(1+g)**(np.arange(1, L+1)/12) #経済成長を模擬
    ratio = value[L-1]/stats.hmean(value) #終値/平均取得金額
    a = np.append(a, ratio)

b= a>1
print("1以上になった数は "+str(np.sum(b))+"回") #1以上の回数を出力

plt.hist(a, bins='auto')
plt.xlim(0.8, 1.2)
plt.xlabel("ratio")
plt.ylabel("frequency")
#plt.savefig('%d.png' %L)
plt.show()

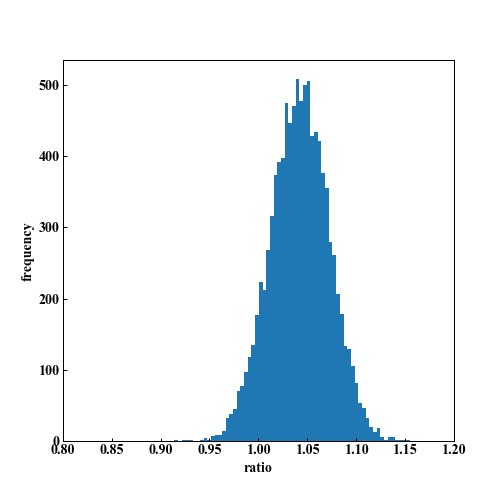
100_2.png
「1以上になった数は 9190回」

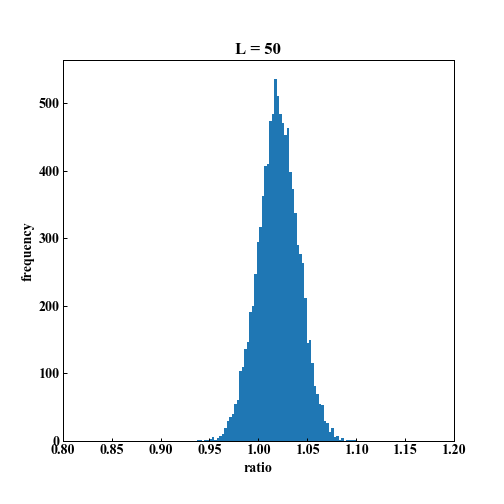
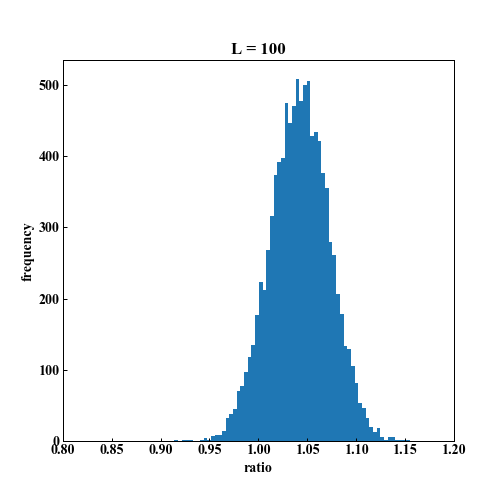
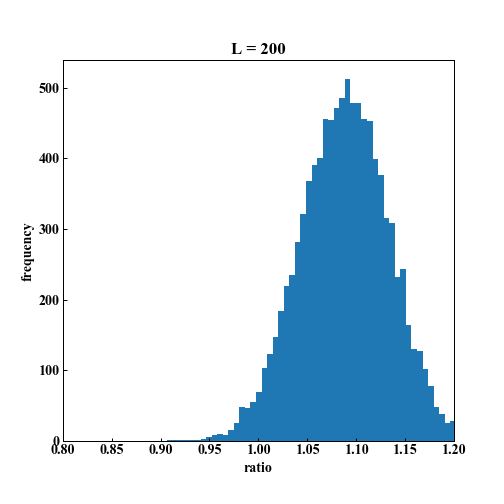
シミュレーション上では、1%の株価の上昇がある場合は、90%以上の確率で勝てることがわかります。
（この確率の値には意味はないですが、確率が高くなることが伝われば結構です）

同条件で、期間Lの影響を調べてみます。
50_L50.png
100_L100.png
200_L200.png

L = 50「1以上になった数は 8400回」
L = 100「1以上になった数は 9190回」
L = 200「1以上になった数は 9733回」

投資の期間が長くなればなるほど、いずれは勝てるゲームになることが予測されます。

逆に言えば、（持株会を含め）投資は気の長いものだということですね。

結論３：経済成長している限りはいつかは儲かる

5. 日本経済はどうなの？

日経平均株価でシミュレーションしてみます。
それなりの企業の株価は、だいたい日経平均株価と連動しているため日経平均株価を使います。

この記事を書いてるタイミングでは、「景気拡大、いざなぎ超え確認　戦後2番目の長さに」なんて言ってますから、期待できるかもしれません。

pandasのDataReader機能を使って、FredからNIKKEI225を引っ張ってきます。
1949年5月16日の開始日から、全ての終値が手に入ります。
これから月初のデータだけ抜き出しておきます。

コード4(日経平均株価)
start = datetime(1949, 1, 1)
end = datetime(2020, 1, 1)
df = web.DataReader('NIKKEI225', 'fred', start, end)

df_m = df['NIKKEI225'].resample('MS').ohlc() #データを月初の値だけ抜き出す
plt.plot(df_m['close'])
plt.xlabel("year")
plt.ylabel("value")
#plt.savefig('NIKKEI225.png')
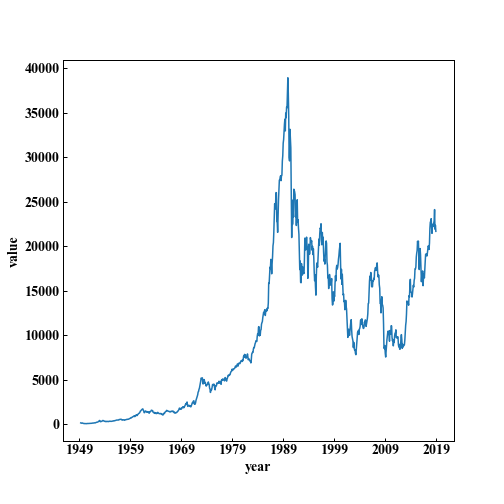
plt.show()

NIKKEI225.png

バブルすごい...　そしてバブル怖い...

バブルの崩壊(1991-1993年)、リーマンショック(2008年)あたりを含め、結構激しい変化があります。

さて、

今までの議論の通り、株価が上がっている時は儲かり、
（バブル崩壊後の）株価が下がってる時は、どうあがいても儲かりそうにないですね。

x年間、毎月持株会で株を買って、すぐに売った場合をシミュレーションしてみます。

コード5(日経でドルコスト平均法)
years = 1
period = years*12
N225 = np.array([])

for i in range(len(df_m)-period):
    N_value = stats.hmean(df_m['close'][i:i+period]) 
    N_ratio = df_m['close'][i+period]/N_value #終値/平均取得金額
    N225 = np.append(N225, N_ratio)

N_b= N225>1
print("1以上になった数は "+str(np.sum(N_b))+"/"+str(len(df_m)-period)+"回") #1以上の数を出力
print("平均倍率は "+str(np.average(N225)))

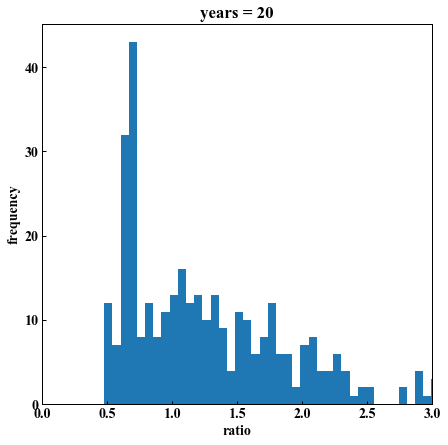
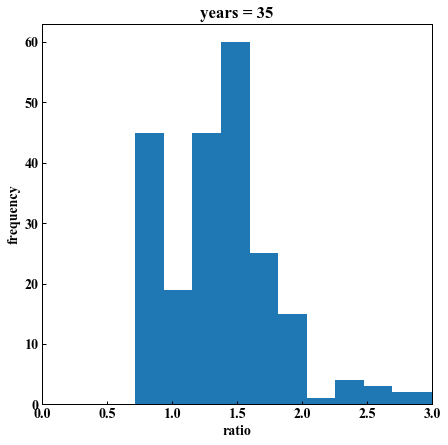
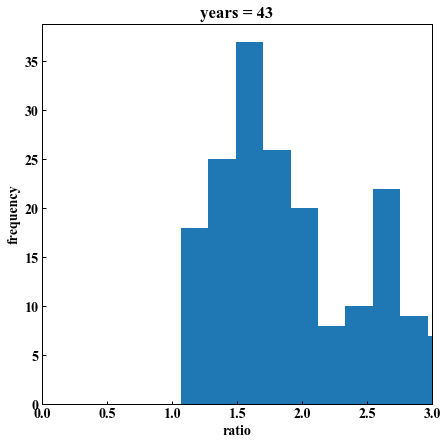
plt.hist(N225, bins=100)
plt.title("years = %d" % years)
plt.xlim(0, 3)
plt.xlabel("ratio")
plt.ylabel("frequency")
#plt.savefig('N225_%d.png' %years)
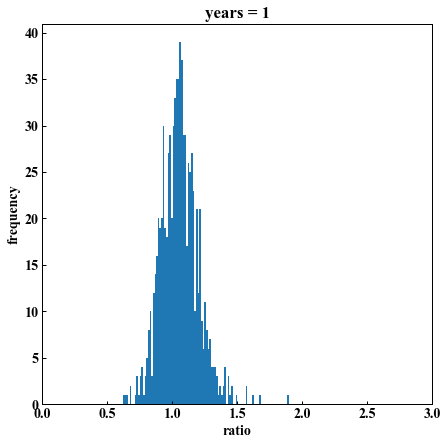
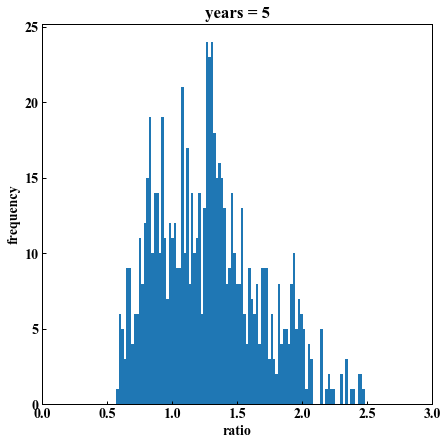
plt.show()

N225_1.png
N225_5.png
N225_20.png
N225_35.png
N225_43.png

years = 1「1以上になった数は 542/824回」 勝率: 66% 平均倍率: 1.06
years = 5「1以上になった数は 561/776回」 勝率: 72% 平均倍率: 1.28
years = 10「1以上になった数は 532/716回」 勝率: 74% 平均倍率: 1.62
years = 15「1以上になった数は 499/656回」 勝率: 76% 平均倍率: 1.93
years = 20「1以上になった数は 460/596回」 勝率: 77% 平均倍率: 2.55
years = 30「1以上になった数は 402/476回」 勝率: 84% 平均倍率: 4.27
years = 40「1以上になった数は 340/356回」 勝率: 96% 平均倍率: 6.32
years = 43「1以上になった数は 320/320回」 勝率: 100% 平均倍率: 5.23

結論４：”43年間”株を買い続ければ絶対儲かる

なるほど！！一生働き続けられるね！！！

投資である以上、絶対はないと思います、念の為。

ちなみに、ここ20年で計算したら、15年買い続ければ勝率100%、倍率1.57でした。

6. まとめ

今回は、持株会をもとに、株で儲かるのかをシミュレーションしてみました。

・ドルコスト平均法は購入単価が安くなる
・儲けの本質は、株価の上昇があること
・長い目で投資すれば、増える可能性が高い

ということを、日経平均株価をもとにして解析できました。
金欲に満たされまくった記事を読んでいただきありがとうございました。

最後に、一言。

投資に必勝法があるとか言ってる奴は信用しないほうがいいと思います。

　　
　　
　　

（気にいったら「いいね」をお願いします！）

　　

参考にした記事など

Pythonのライブラリpandas_datareaderでデータを取得する
・pandas_datareaderの使い方です。

ドルコスト平均法をシミュレーションしてみた
社会の問題をデータ分析でーインベスターZに出てきたロスカットルールを日経平均で試すー
・Qiitaの記事です。どうやって解析しようかとか、ネタが被りすぎないようにという点で参考にしています。

ドルコスト平均法の数学I
・ドルコスト平均法について、数学的に説明という点で勉強になりました。

従業員持株会を【完全ガイド】｜メリットとデメリットも「全て」教えます
・持株会について知りたい人向け。

積立計算(複利毎課税)
・積立投資をしたときに、どれくらいになるか妄想するために使いました。

  1. メリットをまとめると、少額から買える、購入手数料もほぼない、奨励金がつく、もちろん配当金もつく、毎月自動で買ってくれるので楽、結果的に貯金できる。経営者側のメリットは、物言わない株主の確保（必ずしもそうとは言えないが）、自社への愛社精神あたりでしょう。一方デメリットは、売りたいときにすぐには売れない、額が大きくなると良くも悪くもリスクが大きくなる、もっと投資がしたいときに上限がある、など。 ↩

24
19
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
24
19