はじめに

前回に引き続いて、次はSVMを勉強した。
性能が良い分類アルゴリズムでよく使われているらしいので、しっかり押さえておきたい。

SVMの定式化

コスト関数

ロジスティック回帰のコスト関数は以下の通りだった。

J(θ)=\frac{1}{m}\sum_{i=1}^{m}-y^{(i)}log(h_θ(x^{(i)})) - (1-y^{(i)})log(1-h_θ(x^{(i)}))

SVMでは、

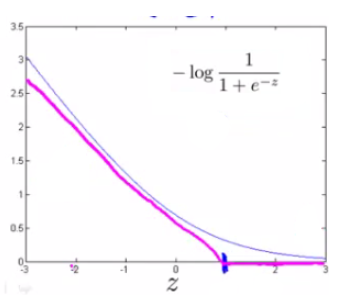
log(h_θ(x)) = log\Big(\frac{1}{1+e^{-θ^{T}x}} \Big)

として、以下のように変更する。

J(θ)=\frac{1}{m}\sum_{i=1}^{m}-y^{(i)}log\Big(\frac{1}{1+e^{-θ^{T}x^{(i)}}} \Big) - (1-y^{(i)})log\Big(1 - \frac{1}{1+e^{-θ^{T}x^{(i)}}} \Big)

$z=θ^Tx$として、

$y=1$の場合
- $z≥1$なら、$cost_1(z)=0$となり、$z$が1よりも小さくなるにつれてコストが大きくなる。

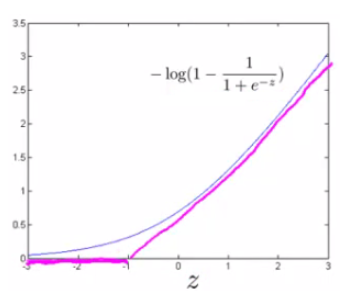
$y=0$の場合
- $z≤1$なら、$cost_0(z)=0$となり、$z$が1よりも大きくなるにつれてコストが大きくなる。

全体にmを掛けて、正則化項を追加することで、最小化したいコスト関数は以下のように表せる。
なおこの時、$C=\frac{1}{λ}$となり、これまでの正則化と同じなんだけど、慣例上SVMの場合はこう書くらしい。

J(θ)=C\sum_{i=1}^{m}y^{(i)}cost_1(θ^{T}x^{(i)}) + (1-y^{(i)})cost_0(θ^{T}x^{(i)}) + \frac{1}{2}\sum_{j=1}^{n}Θ_j^2

折れ曲がったグラフの形から、これはヒンジ損失と呼ばれる。

分類結果

また、SVMの分類結果は以下の通りとなる。

\begin{equation}
 h_θ(x)= \left \{
 \begin{array}{l}
 1　if　θ^Tx≥0 \\
0　otherwise
 \end{array}
 \right.
 \end{equation}

コスト関数がやっていること

直感的に理解するために、Courseraの図をちょっと借用して…

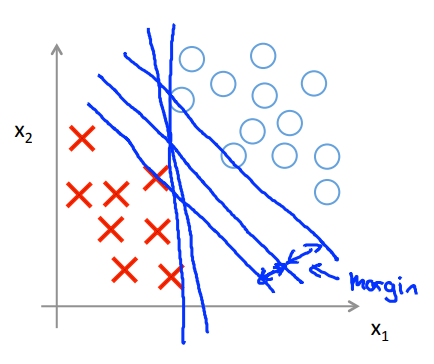
分類でやりたいことは、異なるグループを分けるための境界を決めてあげること。
なので、下図に引かれている境界は全てサンプルをうまく分割できているように見える。

ただ、ほぼ垂直に引かれた境界は、どうもぎりぎりのところを通っているので、あまり良いモデルではないように思えるため、よりきれいに分割できるようなモデルとしたい。

SVMがやっていることは、境界となる平面と、一番近いサンプル点とのマージンの最大化と言い換えることができる。

そこで、境界から反対側に外れている予測結果に大きなコストを与えるのに加えて、うまく予測できているけど、あまりに境界に近すぎるような点にもコストを与えている。

ヒンジ損失のグラフで、コストが増加し始めるのが0ではなく-1 or 1 となっているのはそのため。

カーネル

SVMで決定境界が非線形となる複雑なモデルを構築することを考える。

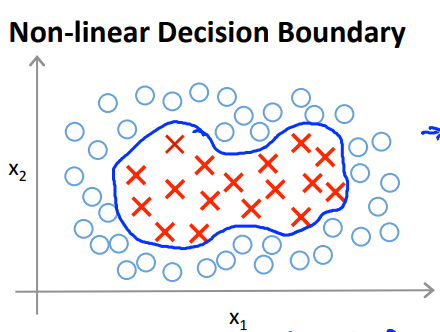
これまでと同じく多項式を使っても良いが、多項式は計算が重くなりがちだし、適切な次数を決めるのも難しい。
そこで、カーネルという考え方が利用されている。

カーネルにはいくつか種類があるらしいが、ここではガウシアンカーネルというものを学んだ。

いくつかのランドマーク$l^{(i)}$を定義し、$x$と$l^{(i)}$の2ノルムを$f_i$として、以下の通り定義する。

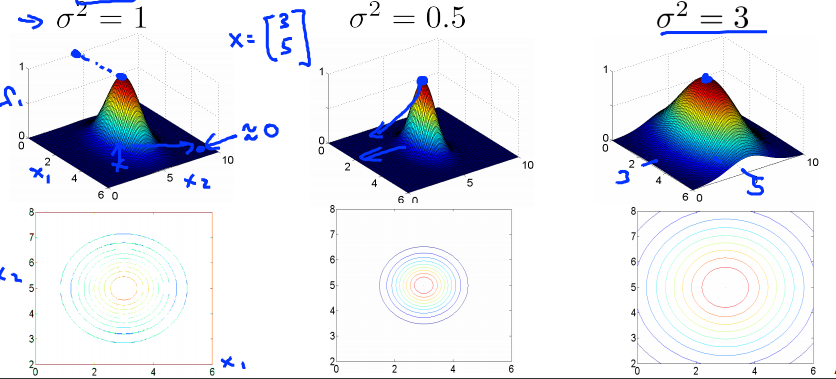
$$f_i = similarity(x, l^{(i)}) = exp(-\frac{||x-l^{(i)}||^2}{2σ^2})$$

$x$と$l^{(i)}$が近ければ、$f_i$は1に近くなるし、遠ければ0に近くなる。

そして、各$f_i$を使って、$h_Θ(x)$は以下のように表される。

f_i = Θ_1f_1+Θ_2f_2+Θ_3f_3+...

ランドマークの決め方

ランドマークの決め方として、元データの$x$をそのまま使うというのがある。
つまり、m個のデータセットについて、

$$l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},l^{(3)}=x^{(3)},...,l^{(m)}=x^{(m)}$$

パラメータの決め方

カーネルを用いたSVMでは、$C$と$σ^2$の2つのパラメータがあり、適切にチューニングする必要がある。

$C$について
$C$はこれまで勉強した正則化でいうところの$\frac{1}{λ}$にあたる。
よって、
- $C$が大きいと高バリアンス、低バイアスになる。
- $C$が小さいと低バリアンス、高バイアスになる。
$σ^2$について
- $σ^2$が大きいと、$f_i$がなだらかになり、低バリアンス、高バイアスになる。
- $σ^2$が小さいと、$f_i$が急になり、高バリアンス、低バイアスになる。

SVMを使う際の注意点

ガウシアンカーネルを使う場合はfeature scalingしておくこと。
特徴量の数が多く、データサンプルが少ない場合は、カーネル無しのSVMを使う。
特徴量が少なく、データサンプルが多い場合は、ガウシアンカーネルを使う。

ロジスティック回帰との使い分け

特徴量がデータサンプル数に対して多い場合 (n=10000, m=10-1000 くらい)
- ロジスティック回帰
- カーネル無しのSVM
特徴量が少なく、データサンプルがそこそこある時 (n=1-1000, m=10-10000 くらい)
- ガウシアンカーネルありのSVM
特徴量が少なくデータサンプルが多い時 (n=1-1000, m=50000以上くらい)
- まずは特徴量を増やすことを考える
- ロジスティック回帰
- カーネル無しのSVM

線形分離できない複雑なデータセットに対してカーネルを使ってこそ、SVMの真の性能が発揮される、ということらしい。
また、ニューラルネットワークは上記のどのパターンでも良い性能が出るけど、大体の場合計算は遅い。

まとめ

数学的なところは結構曖昧にしか理解できていないけど、直感的には何をしているかイメージできた。
根強く人気のアルゴリズムのようだし、実際に使いながら理解していきたい。

コースの主な山場を越えて、やっと完走が見えてきた。

Coursera Machine Learningのまとめ(SVM編)