【ICLR2019】Solving the rubik's cube with approximate policy iteration

この記事は「ICLR2019を読むアドベントカレンダー」の13日目の投稿記事です。記事の前半は機械学習の知識がなくても読めますが、後半は強化学習の知識が必要です¹。

今回取り上げる記事はICLR2019に投稿されている次の論文です。
Solving the Rubik's Cube with Approximate Policy Iteration
ArXivには少しタイトルを変えて投稿されています。
S. McAleer et al. (2018), Solving the Rubik's Cube Without Human Knowledge

論文の内容は、去年の10月に公開された AlphaGo Zero の論文
D. Silver et al. (2017), Mastering the game of Go without human knowledge
で使用されている手法を適用して Rubik's Cube を解いてみましたという内容です。単に手法を Rubick's Cube に適用してみるだけではなく、学習の際に Autodidactic Iteration と名付けられた新たな手法を導入することによって学習の安定性を高めた点が重要な貢献となります。

今の所この論文を実装したWebsiteは公開されていますが、そのソースコードは公開されていません。この論文の著者はOpenReview上で、論文がAcceptされた際にはソースコードを公開すると言っていますが、まだされていません。代わりに、今回自分がこの論文を読むにあたって細かいところを確認するために行なった実装を公開していますので参考にしてください。

概要

Rubick's cube を解くアルゴリズムというのはすでにあるようで、例えば Kociemba Algorithm と呼ばれるものが有名だそうです。ただし、それらのアルゴリズムは Rubik's Cube の対称性などの情報を駆使して人間が特別にデザインしたもので汎用性はありません。この論文はそのような事前知識をアルゴリズムに与えずに、学習のみで Rubik's Cube を解くことができるかどうかという問題を解いたものです。

提案されている手法(DeepCubeと名付けられている)は簡単な手法にいくつかの改善が段階的に適用された手法になっているので、その改善点を順を追って説明していきたいと思います。まず、Rubik's Cube を解くアルゴリズムとして最も簡単なものは全探索だと思います。下図²のように、与えられた Rubik's Cube に対して任意の操作を順に調べていくことで、いつかは正解の手順を見つけることができます。しかし、この手法は探索量が膨大になりすぎるので実際に解く時に使用するのはほとんど不可能です。

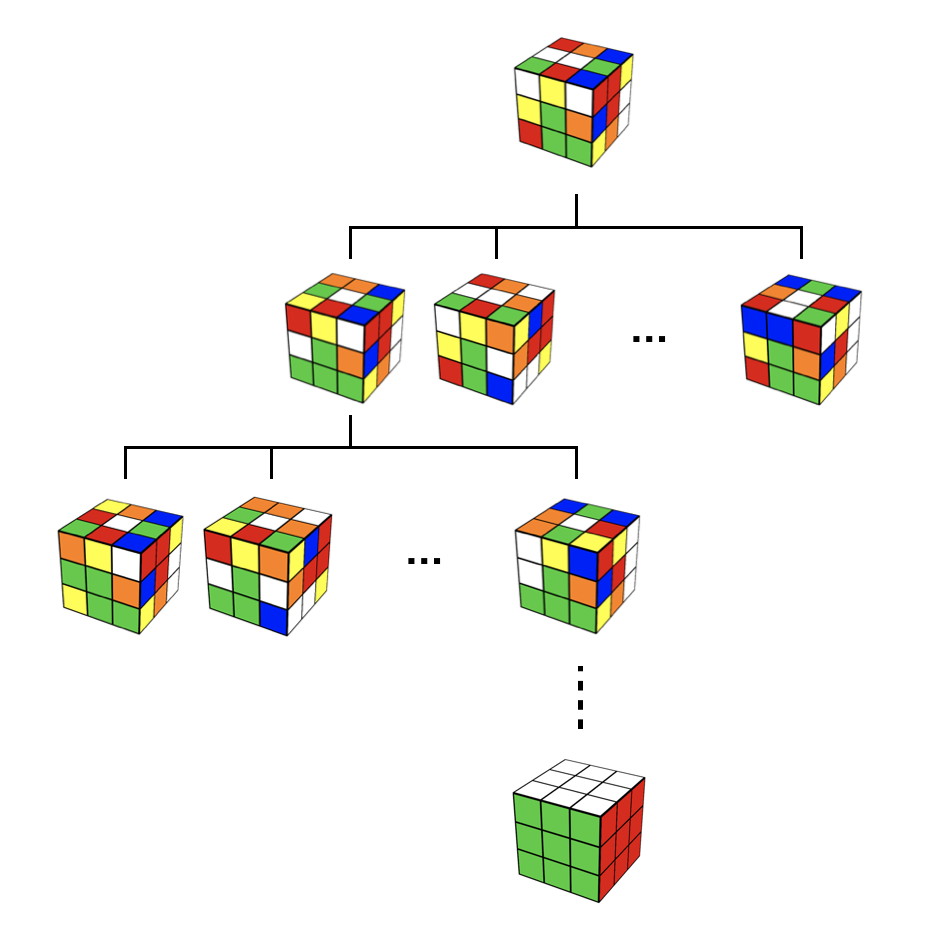
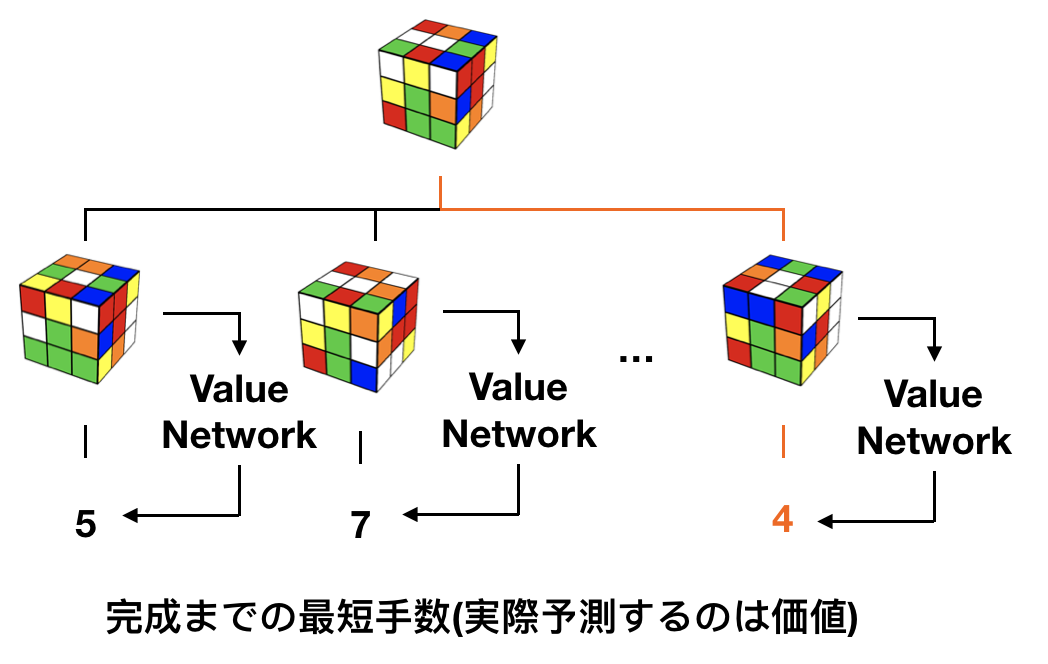
探索量を減らすための一つ目の工夫として、まず、それぞれの状態の Rubik's Cube を最短で何手で完成の状態に持っていくことができるのかを予測できるような予測機 Value Network を作ることを考えます。このような予測機を作るのは難しそうですが、もし作ることができれば各状態から、一番完成までの手数が少なくなりそうな状態に移行できるような操作を行なっていけば、いずれ最短の手数で Rubik's Cube を完成させることができます。下の図では、一番右側の操作が完成までにかかる手数が一番少ないので、明らかに一番右の操作を行うのが完成までの近道です。実際には Value Network は完成までの最短手数ではなく、それと線形の関係にある、状態の価値と呼ばれる値を予測することになりますが、行なっていることは変わりません。

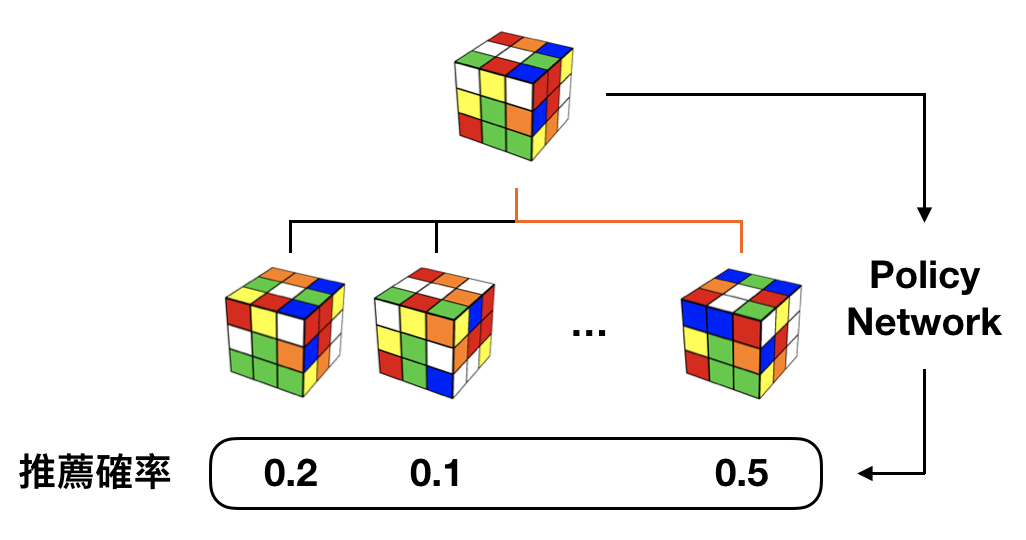
Rubik's Cube を解くだけならばこれだけでも十分に解ける気もしますが、もともと探索量がもっと広い囲碁を解くための手法だったものを改造しているので、さらに二つの目の工夫が備わっています。先の Value Network を使った手法は、一度操作を選ぶためには可能な操作の数だけ Value Network を評価しなければならないことがわかります。なぜなら、どの操作が最も手数が少なくなりそうかは、任意の操作を加えた後の状態それぞれに対して Value Network を評価しなければわからないからです。上図でも、可能な操作全てに対して Value Network を評価していることがわかると思います。そこで、Value Network による評価を行うべき状態を推薦する予測機 Policy Network を新たに作成して、Policy Network で推薦された状態だけに対して Value Network を評価するようにします。推薦された操作だけに対して Value Network を評価すれば良いので、探索効率がグッとよくなります。

ここまでの改善で探索量自体はだいぶ減りました。予測機 Value Network と予測機 Policy Network が完璧に動作するならば、以上の二つの工夫だけで Rubik's Cube を最短手数で解くことができるはずです。ただしそこまで完璧な予測機を作ることは難しく、大抵は予測機が少し間違っていたりします。そのような場合を考え、少しくらい予測機がおかしな予測をしてもアルゴリズムがうまく動くようにいくつか fail safe のための工夫を入れています。それが論文の本文で Monte Carlo Tree Search (MCTS)と呼ばれているものです。

以上の3つの工夫(Value Network, Policy Network, MCTS)を加えることによって、全探索と比べるととても小さな探索量で Rubik's Cube を解くことができるようになります。これら3つの手法はすでに AlphaGo Zero で提案されている手法ですが、今回取り上げた論文は　Value Network と Policy Network の学習の方法に一工夫加えたものになっています。

Value Network の構築

Value Network は Rubik's Cube の各状態に対して、そこから完成までの最短手順数を予測できる必要があります。そのような予測機を作成するにあたって重要なのが、Rubik's Cube は強化学習における Markov Decision Process (MDP)として解釈できると言う点です。具体的には Rubik's Cube は次のようなMDPとして解釈することが可能です。

• 状態集合: Rubik's Cube が取りうるすべての状態
• 行動集合: Rubik's Cube に対して取りうるすべての操作
• 遷移確率: 決定論的に、ある状態からある操作を受けた時の次の状態が決まる。
• 報酬関数: 解けた時+1, 解けていない時-1

このような Rubik's Cube とMDPとの対応を見つけることがわかれば、最短手数を予測するための良い手段として、強化学習で言うところの最適価値関数がうまく使えることがわかります。このMDPでの最適価値関数は、完成の状態では値1を、完成から一ステップ前では0を、二ステップ前では-1を, ... とるはずなので、少し変換してやればそのまま最短手順数を指し示してくれることはわかります。

最適価値関数をMDPから近似的に作成する方法は強化学習の方でよく調べらているので、とりあえず Value Network を Neural Network で構築して、有名なTD学習¹を行えば、最短手数を予測することのできる Value Network が近似的には作れそうです。また、off policy 学習¹を使用することで、学習用のデータの生成と学習自体を同時に行う必要がなくなっています。

Policy Network の構築

概要でも説明した通り、Policy Network は各状態に対してどの操作を加えた状態を先に探索した方が良いかを推薦する役割をもつ予測機です。よって、基本的には完成までの手数が少なくなりそうな操作を推薦すべきです。

この予測機の構築は、Value Network が十分に高い精度で任意の状態に対する最短手数を予測できて入れば簡単に構築できます。単純に、与えられた Rubik's Cube の状態に対して任意の操作を行なってみて、それぞれの完成までの最短手数が最も小さいものを推薦するように学習すれば良いわけです。これも Value Network と同様に Neural Network で構築して、Value Network の出力をもとに学習してしまうことにします。

Value, Policy Network の学習の工夫

強化学習アルゴリズムにおける学習は、教師あり学習ほど簡単ではありません。特に今回のような Rubik's Cube が解けた場合のみしか報酬の変化がないような場合には、あまりにfeedbackが少なすぎて学習できないことが多いです³。そのような問題に対処するために、この論文では Autodidactic Iteration と言うアルゴリズムを導入して学習を進ませています。

詳細は論文をみていただくとして、重要な点は次の二点です。

1. Rubik's Cube が解けている状態から学習用のデータを作り始めることで、学習中に Rubik's Cube が解けている状態が頻度高く現れるようにする。
2. Neural Network を学習する際のコスト関数に、Rubik's Cube が解けている状態のコストを強く反映させる。

上記の二つによって、Rubik's Cube が解けている状態(報酬が+1の状態)が、解けていない状態(報酬が-1の状態)と比べてもある程度重視されるようになり、学習がうまく進むようになります。

また、Value Network と Policy Network の低い層は学習後、似たような特徴抽出を行うことになると予想されるので、それらの層は共通のnetworkとして構築しているようです(論文の本文の Supplementary B)。

MCTS の手順

最後に、学習を終えた Value Network と Policy Network を使って、与えられた Rubik's Cube を完成させていきます。基本的には、与えられた Rubik's Cube の状態からなんども探索を繰り返して、完成にたどり着いたら終了するという戦略をとります。その途中で、何度も探索たびに同じ操作ばかりを探索していては埒があかないので、何回か探索した操作はあまり同じ操作が行われないようになっていくような調整を入れています。

まず、1回目のトライアル。与えられた Rubik's Cube 自体がすでに完成している場合はそれで終了します。多くの場合はそうではないので、次のトライアルでどの操作を探索するかを Policy Network を評価することで決めておきます。

次の2回目のトライアルでは、先の Policy Network による評価を使って一つ深く探索します。もしこの状態で完成している場合はアルゴリズム終了ですが、そうでない場合には Value Network の評価を行い、実際その操作をしたらどれくらい完成に近づくのかをfeedbackします。

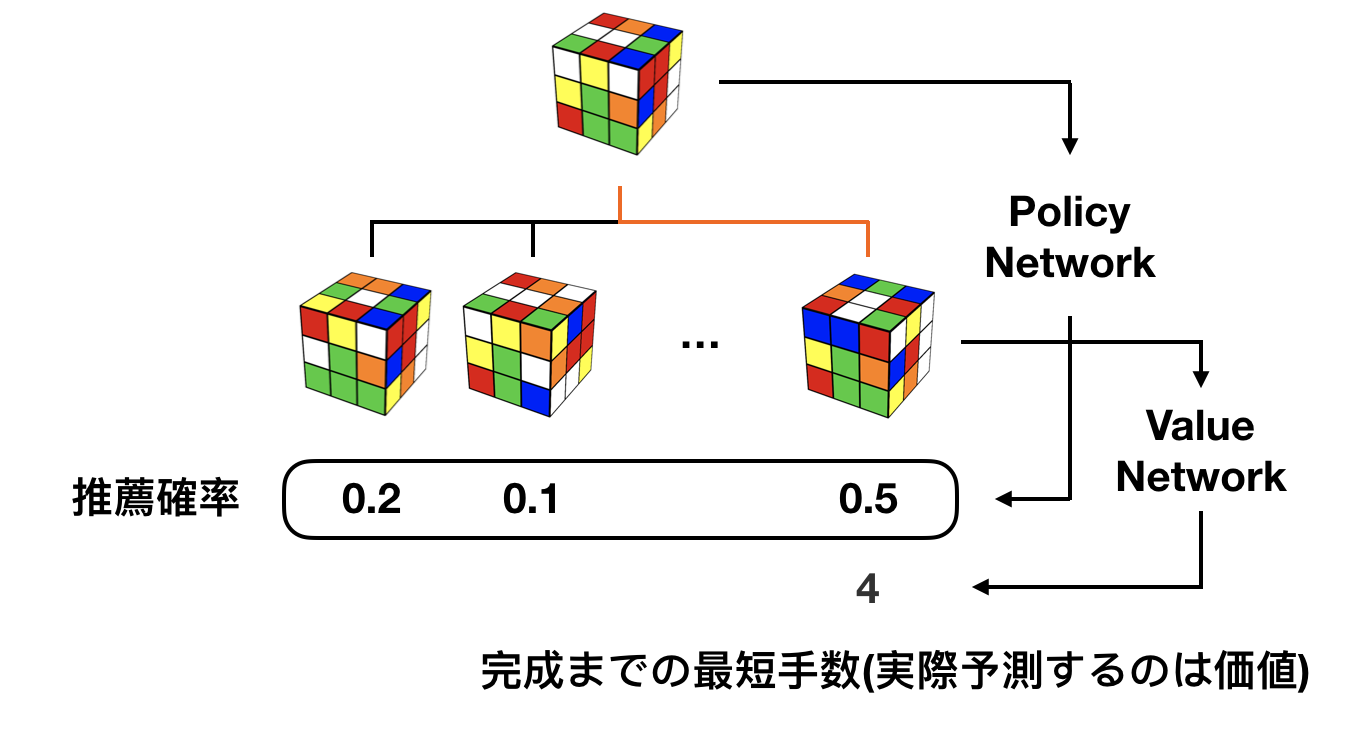
次の3回目のトライアルでは、先の Value Network による評価$W$と前から存在する Policy Network による評価$P$を使って、次の評価関数を最大にするような操作$a$を探索します。
$$
W(a) + c_{puct} P(a) \frac{\sqrt{\sum_a N(a)}}{1 + N(a)}
$$
ここで、$N(a)$はその操作を今までに何回行ったかを指す数です。二項目の$N(a)$に依存する部分$\sum_a N(a) / (1 + N(a))$は、トライアル数が多くなるにつれて平均的に小さくなっていくため、トライアル数が少ない場合には Policy Network の出力$P$を重視して、トライアル数が大きくなっていくにつれて Value Network の出力によるもの$W$を重視するような評価関数になっています。これは Policy Network が、各状態ごとに Value Network をありえる操作の数だけ評価すると時間がかかるから導入した、という経緯を考えれば自然なことです。このような探索方法をPUCTアルゴリズムと呼ぶそうです。そして、探索してたどり着いた先でさらにそれより深い状態を考慮に加えていきます。

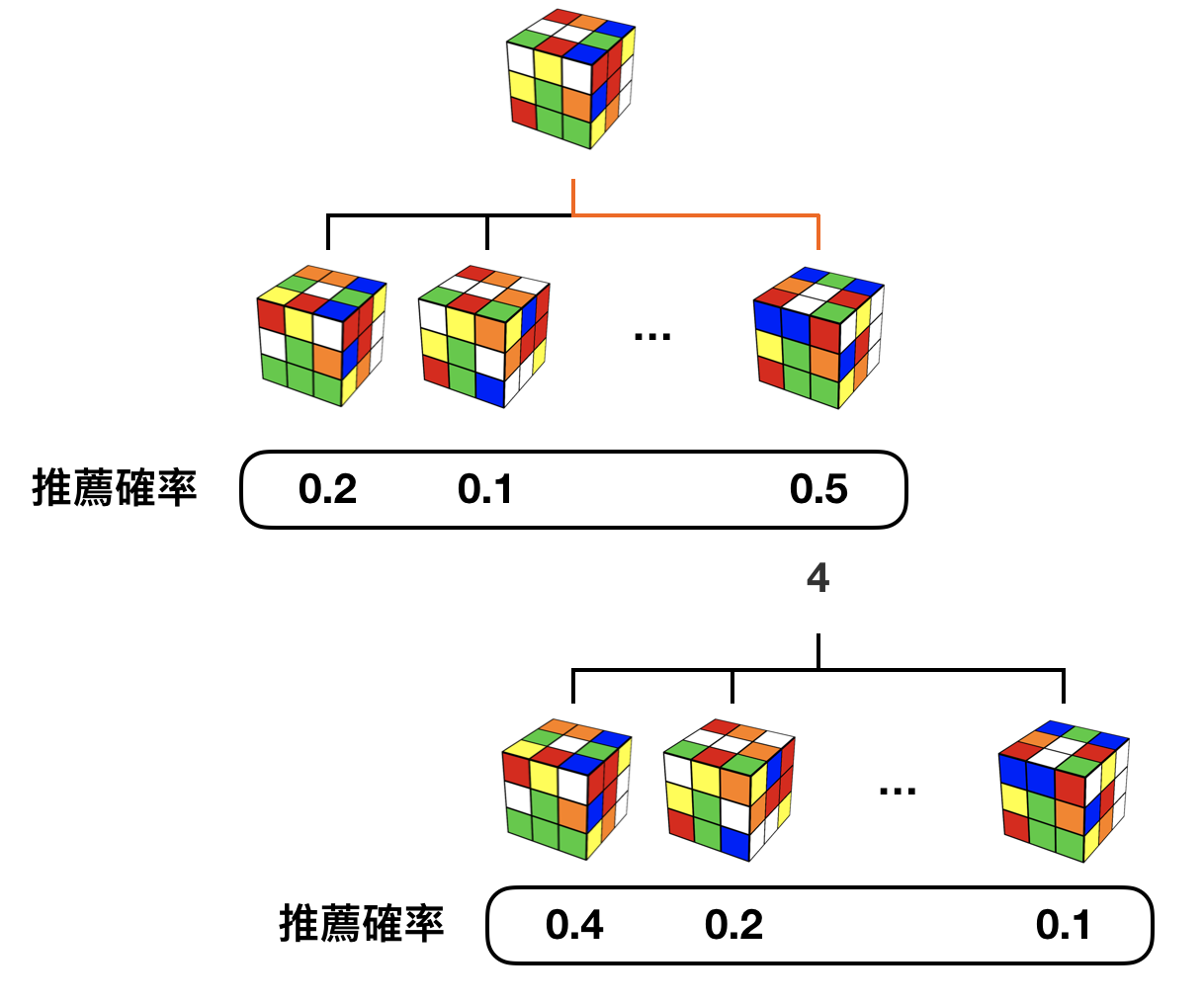
以上のように、

1. Policy Network による探索方向の簡易選択
2. その簡易選択を使って、実際に探索する
3. 探索した先で Value Network を評価して、その簡易選択の結果をPUCTアルゴリズムで洗練させる。
4. 再度の探索

という手順を繰り返していき、完成している状態にたどり着いたらそこでアルゴリズムが終わるように設計されている。

気になった点

一つ目は、 Rubik's Cube のMDPとしての定義が曖昧な点が気になりました。細かいことを言えば、Rubik's Cube をMDPと見る見方は二つほどあります。一つは完成した状態を終端状態としてそれでエピソードが終わると考える見方、もう一つは完成してもまだエピソードは続いていてその先も何かしら操作をしていくと考える見方の二つです。実際の論文は後者で説明しているように読み取れます。

実装した際、最初は完成した状態は終端状態ではないと思って実装していましたが、 Value Newtork の予測値自体が発散してしまいました。そのあと完成した状態が終端状態だと思って実装をした場合には Autodidactic Iteration を使えばまったく発散せず自然に収束しました。著者は論文がAcceptされたらソースコードを公開すると言っているので、実際にはどうやって実装しているのかをみてみたいところです。

二つめは、MCTSの探索で使用されているPUCTアルゴリズムの導き方がどこをみても書いていないのが気になりました。そのアルゴリズムはAlphaGo Zero の論文で最初に紹介されているようですが、そこで引かれている参考文献がどうPUCTアルゴリズムと繋がっているのかわからず、色々と調べましたが⁴どれもPUCTアルゴリズムがどういう導き方をされているのかが書かれたいなかったので、パラメータ調整などもあまりできず大変でした。そもそもPUCTがなんの略称なのかも議論があるようで、Polynomial Upper Confidence Tree だったり、Policy + UCT だったり色々でよくわからなかったです。

1. 強化学習について軽く知りたい人は強化学習入門 by BrainPadなど日本語の記事を、深く知りたい人はReinforcement Learning by R. Suttonなどの教科書を読むと良いと思います。 ↩ ↩² ↩³

2. Rubik's Cube の画像は、DeepCubeのwebsiteの Rubik's Cube の背景色のみ可能して使わせていただいています。 ↩

3. Deep Reinforcement Learning Doesn't Work Yetでも、"Currently, deep RL isn’t stable at all, and it’s just hugely annoying for research."と言及されています。 ↩

4. とある Google Group での議論スレッドとか、GithubレポジトリでのIssueとか。 ↩