Python で物理定数を使う scipy.constants 〜定数 e 〜

#0. 環境

$\bullet$ macOS Catalina
$\bullet$ Jupyter notebook
$\bullet$ Python 3.8.6
$\bullet$ NumPy 1.18.5
$\bullet$ SciPy 1.5.4¹

#1. scipy.constants
##1.1 物理定数
from scipy.constants import * とすることで物理定数を導入できます．

SI_2019

from scipy.constants import * 
print(physical_constants["hyperfine transition frequency of Cs-133"])
print(c) #speed of light in vacuum
print(h) #the Planck constant
print(e) #elementary charge
print(k) #Boltzmann constant
print(N_A) #Avogadro constant
print(physical_constants["luminous efficacy"])

出力結果です．

Results

(9192631770.0, 'Hz', 0.0)
299792458.0
6.62607015e-34
1.602176634e-19
1.380649e-23
6.02214076e+23
(683.0, 'lm W^-1', 0.0)

from scipy import constantsとした場合,constants.hやscipy.constant.physical_constants["hyperfine transition frequency of Cs-133"]などとしなければなりませんが，同様の結果が得られます．

from scipy import constants
print(constants.h)
#6.62607015e-34

##1.2 より細かい計算

更に，併用単位などの様々な単位も計算に使うことができます．

units

from scipy.constants import * 
print(day) #one day is 86400 seconds
print(gram) # one gram is 0.001 kilogram
print(eV) #1 eV equals e coulomb times 1 volt
#86400.0
#0.001
#1.602176634e-19

接頭辞を用いた単位計算も可能です．lambda2nu()を使うことで電磁波の波長ー振動数の換算をすることもできます．

prefix_and_lambda2nu

print('{:e}'.format(lambda2nu(370 * nano)), 'Hz') #ultraviolet
print(lambda2nu(370 * nano) / tera, 'THz')
print('{:e}'.format(lambda2nu(1 * milli)), 'Hz') #radio waves (microwaves)
print(lambda2nu(1 * milli) / giga, 'GHz')
#8.102499e+14 Hz
#810.2498864864865 THz
#2.997925e+11 Hz
#299.792458 GHz

#2. 定数 e

##2.1 電気素量とネイピア数

電気素量とネイピア数は記号がどちらも同じ $e$ で紛らわしいです²．

印字するだけなら注釈をつければよいですが，コード中では同じ名称はつかえません．

from scipy.constants import * 
print(physical_constants["elementary charge"])
print(e)
print(math.e) #the Euler's number

特に LaTeX ではmath.eなんて打つことはありませんから，清書された数式を Python のコードに写す場合などは非常に面倒くさいです．

##2.2 e の累乗の例: Fermi-Dirac 統計

準備

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.constants import *

指数が登場する例として，Fermi-Dirac 分布を考えます．以下の式のグラフをプロットしたいとします：

 \frac{1}{e^{\beta(\varepsilon - \mu)} + 1}= \frac{1}{e^{\mu(x - 1)/(kT)} + 1}\quad(x = \varepsilon/ \mu )

ここで，$ k $ は Boltzmann 定数です．Jupyter notebook で描いてみましょう．

Fermi_Dirac_distribution

from scipy.constants import * 
def E(x, mu):
    return 1/(e**(mu*(x - 1)/(k*T)) + 1)

あれ，おかしなグラフになってしまいました (グラフの描画設定は省略しています)．これでは粒子がいくらでも高いエネルギーを取れることになりますから，定性的にありえないグラフになっています．from scipy.constants import *でeが電気素量の値として定義されているため，グラフは出力されたものの，計算が間違ってしまったのです．

もちろんimportをいじくって解決してもよいのですが，ここでは最も直感的・簡便・便宜的な方法を採用します．つまり，今は数式に合わせて

e = math.e

としてしまいましょう．今回の計算に電気素量は用いていませんから，局所的にはこれで問題ありません (電気素量を別のところで用いることになれば，その時にfrom scipy.constants import *を再度書くなどすればよいでしょう)．

from scipy.constants import * 
e = math.e
def E(x, mu):
    return 1/(e**(mu*(x - 1)/(k*T)) + 1)

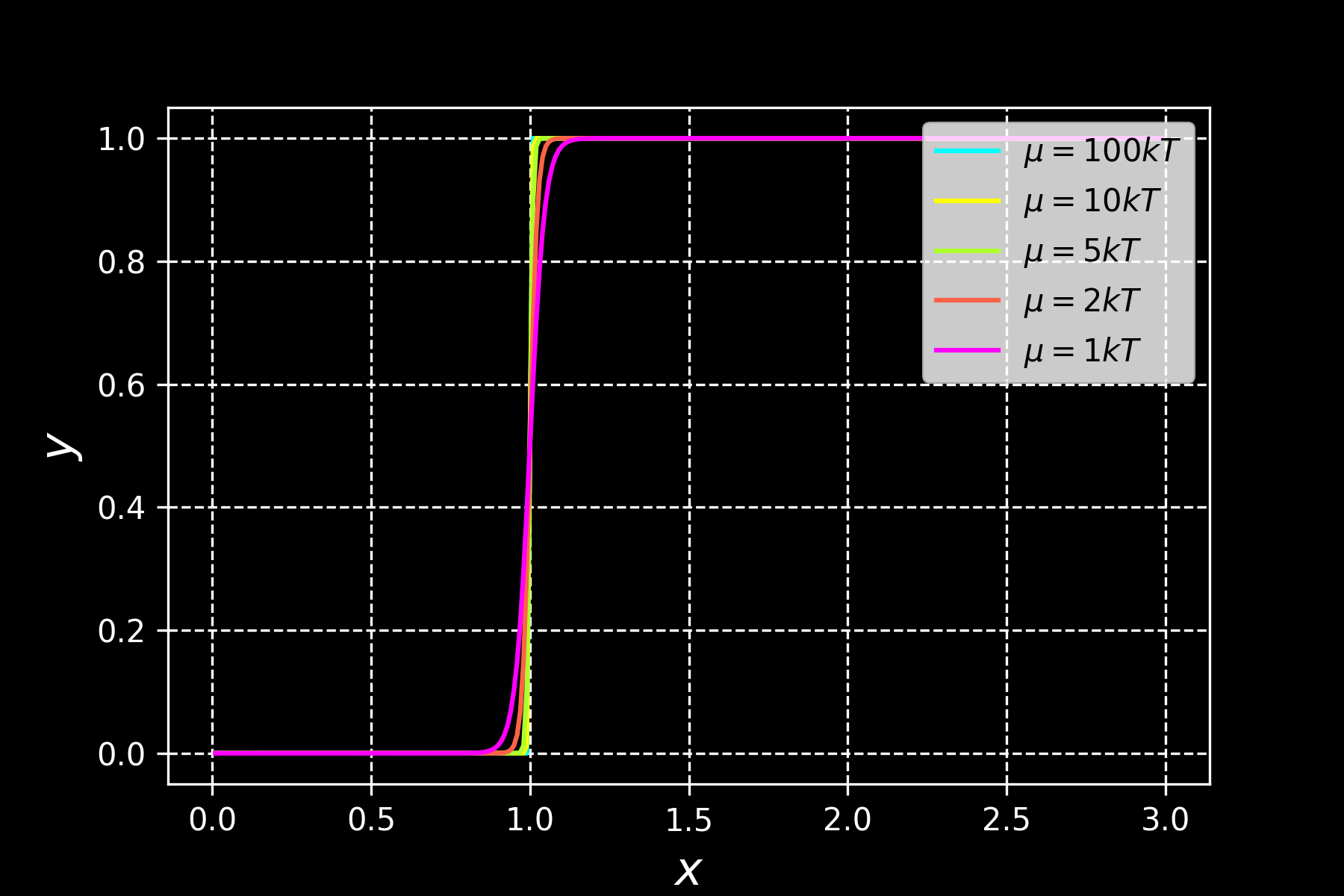
正しいグラフが出力されました！

#関連・参考記事
Constants (scipy.constants) — SciPy v1.5.3 Reference Guide
[SciPy Constants]
(https://www.w3schools.com/python/scipy_constants.asp)
[Python math.e Constant]
(https://www.w3schools.com/python/ref_math_e.asp)
[python memo]
(http://tomohiro_abe.droppages.com/misc/python.html)　`from scipy.constants import * `について参考にしました．
[Fermi–Dirac statistics - Wikipedia]
(https://en.wikipedia.org/wiki/Fermi–Dirac_statistics)　Fermi-Dirac 統計について参考にしました．

1. print(scipy.constants.physical_constants["hyperfine transition frequency of Cs-133"])やprint(scipy.constants.physical_constants["luminous efficacy"])が空列として出力される場合はアップデートが必要です．SciPy 1.4.0 Release Notes — SciPy v1.5.4 Reference Guide ↩

2. eやiのように立体にする流儀もありますがすべての場合でそうなっているわけではなく，むしろ慣例的には斜体のほうが用いられます． ↩