東大学際科学科B群4年のSyumeiです。卒論に余裕ができたので、趣味で作っていたソフトフェアデバックツールについて記事を書いてみます。備忘録的な内容なので、実装の詳細などはかなり省略しています。
0 概要
本記事では、ソフトウェアテストの代表的な手法であるシンボリック実行を、c++を用いて、外部ライブラリを使わずにフルスクラッチで実装します。シンプルな機能を実装するだけならつまらないので、勾配降下法を用いた制約解決、ニューラルネットワークが埋め込まれたプログラムのデバック、確率的ソフトフェアのデバックなどの要素を埋め込んでみました。
本プロジェクトのコードは以下のレポジトリで管理しています。
なお、このツールは完全に趣味で作成しており、正確さについての保証はありません。既存の有名なツールよりも高速というわけではありません
1. シンボリック実行とは何か?
シンボリック実行とは、プログラムの入力として具体的な値を与える代わりに、値を代表するシンボル(記号)を与えてプログラムを模擬的に実行し、その結果を評価する手法です。
具体的には、プログラムの各変数をシンボルとして扱い、代入や演算によって変数が伝搬していく様子を、条件分岐を判定しながら追跡していきます。判定が真になる場合と偽になる場合の2ケースに分けて実行することで、すべての実行可能なプログラムパスを網羅することができます。
シンボリック実行を用いると、以下のような作業が可能になります。
- 広範なパスの探索: 全ての可能な入力や実行パスを探索することができます。
- 異常な挙動の検出: プログラムが意図しない挙動を示す可能性がある箇所を見つけることができます。
- 自動テストケース生成: シンボリック実行を使用して、異なるパスをテストするための入力を自動的に生成できます。
例えば以下のようなプログラムを考えます。
if (x < 3) {
if (x > 1) {
return 1;
} else {
return 2;
}
}
このプログラムでは、xという変数の値に応じて、1もしくは2を返します。ここで、xがどのような値であるときに1を返し、どのような時に2を返すのでしょうか? そもそも、各条件分岐に到達するような入力は存在するのでしょうか? シンボリック実行を用いると、このような問題を自動的に解いてくれます。
2. 勾配降下法を用いたパス制約解決
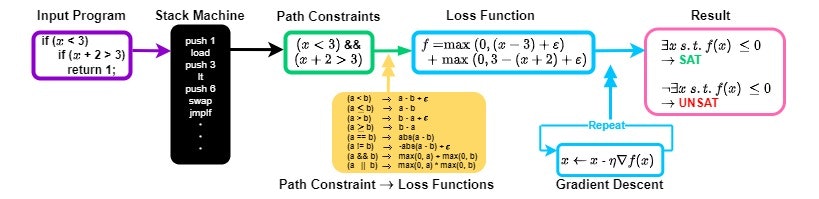
(x < 3) && (x > 1)を満たすようなxを求める、というような問題はSMT Solver等で解くことができますが、これを勾配降下法で解くことも(近似的に)可能です。具体的には、比較条件を以下のような関数に置き換えます。
!(a) => -a + eps
(a < b) => a - b + eps
(a <= b) => a - b
(a > b) => b - a + eps
(a >= b) => b - a
(a == b) => abs(a - b)
(a != b) => -abs(a - b) + eps
(a && b) => max(a, b)
(a || b) => min(a, b)
ここで、epsはaおよびbがとりうる値の絶対値の最小値 (例えば整数なら1)を意味します。
こうすることで、制約条件を、その条件が満たされるときは0以下を、満たされないときは正の値を返すような損失関数に置き換えることができます。この損失関数が0以下になるような入力は、勾配降下法で求めることができます (もちろん、局所解にはまって解が存在するにもかかわらず発見できない可能性はある)。
3 実装の概要
入力プログラムの文法
このツールは以下のBNFを持つ、C言語ライクなプログラムを想定しています。
program = stmt*
stmt = expr ";"
| "{" stmt* "}"
| "if" "(" expr ")" stmt ("else" stmt)?
| "return" expr ";"
expr = assign
assign = logical ("=" assign)?
logical = equality ("&&" equality | "||" equality)*
equality = relational ("==" relational | "!=" relational)*
relational = add ("<" add | "<=" add | ">" add | ">=" add)*
add = mul ("+" mul | "-" mul)*
mul = unary ("*" unary | "/" unary)*
unary = ("+" | "-")? primary
primary = num | ident | "(" expr ")"
シンボリック実行の基本的な流れとしては、入力プログラムを疑似的にコンパイルしてスタックマシンに変換し、そのスタックマシンを実行しながら各制約条件を満たすような入力が存在するかを、勾配降下法を用いて検証していくという流れになります。コンパイラの部分はrui314/chibicc、スタックマシンを用いたシンボリック実行はbeala/symbolicを参考にしました。
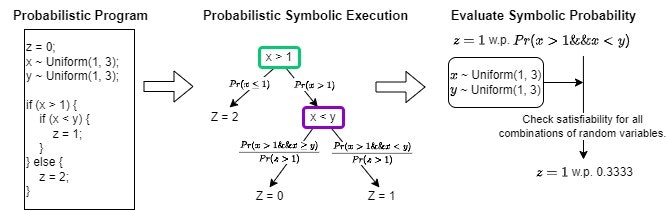
さらに、Susag, Zachary, et al. "Symbolic execution for randomized programs." Proceedings of the ACM on Programming Languages 6.OOPSLA2 (2022): 1583-1612.で提案されているアルゴリズムを参考に、離散有限確率分布に従う変数も部分的に処理できるようにしました。
この手法では、乱数を含む制約条件を記号的に処理することで、大量のサンプリングなどを行うことなく、出力の確率的な性質(期待値、分散等)を正確に求めることができます。
4 使用例
このツールは、コマンドラインツール、C++のヘッダーオンリーライブラリおよびそのPython APIの形で配布しています。レポジトリのExamleに、実行用スクリプトをいくつか置いています。
- コマンドラインツールのインストール
git clone https://github.com/Koukyosyumei/Gymbo.git
cd Gymbo
./script/build.sh
- コマンドラインツールの使用例
上記のスクリプトを実行すると、gymboというコマンドラインツールが生成されます。このツールは入力プログラムを受け取り、そのプログラム中の各制約条件を検証します。詳細なオプションはGitHubのREADMEに記載してあります。
>./gymbo "if (a < 3) if (a > 4) return 1;" -v 1
Compiling the input program...
Start Symbolic Execution...
pc: 0, push 0
pc: 1, load
pc: 2, push 1077936128
pc: 3, lt
pc: 4, push 6
pc: 5, swap
pc: 6, jmpIf
pc: 10, push 1082130432
pc=10, IS_SAT - 1, Path Constraints: (var_0<3), params = {0: -3, }
pc: 11, push 0
pc: 12, load
pc: 13, lt
pc: 14, push 6
pc: 15, swap
pc: 16, jmpIf
pc: 20, ret
pc=20, IS_SAT - 0, Path Constraints: (var_0<3)&&(4<var_0), params = {}
pc: 17, nop
pc=17, IS_SAT - 1, Path Constraints: (var_0<3)&&!(4<var_0), params = {0: 2, }
pc: 18, push 2
pc: 19, jmp
pc: 21, ret
pc: 7, nop
pc=7, IS_SAT - 1, Path Constraints: !(var_0<3), params = {0: 7, }
pc: 8, push 12
pc: 9, jmp
pc: 21, ret
---------------------------
Search time is complete 0.000000 [ms]
Result Summary
#Loops Spent for Gradient Descent: 0
#Total Path Constraints: 4
#SAT: 3
#UNSAT: 1
List of SAT Path Constraints
----
Path Constraints: !(var_0<3)
SAT Params: {var_0:7, }
----
Path Constraints: (var_0<3)&&!(4<var_0)
SAT Params: {var_0:2, }
----
Path Constraints: (var_0<3)
SAT Params: {var_0:-3, }
----
List of UNSAT Path Constraints
Path Constraints: (var_0<3)&&(4<var_0)
----
- ライブラリの使用例
ヘッダーオンリーライブラリのドキュメントに、簡単な説明があります。
#include "libgymbo/compiler.h"
#include "libgymbo/gd.h"
#include "libgymbo/parser.h"
#include "libgymbo/tokenizer.h"
#include "libgymbo/type.h"
char user_input[] = "if (a < 3) return 1;"
std::vector<gymbo::Node *> code;
gymbo::Prog prg;
gymbo::GDOptimizer optimizer(num_itrs, step_size);
gymbo::SymState init;
// tokenize the input source code
gymbo::Token *token = gymbo::tokenize(user_input);
// generate AST from the tokens
gymbo::generate_ast(token, user_input, code);
// construct virtual stack machine from AST
gymbo::compile_ast(code, prg);
// execute gradient-based symbolie execution
gymbo::SExecutor executor(optimizer, maxSAT, maxUNSAT, max_num_trials,
ignore_memory, use_dpll, verbose_level);
executor.run(prg, target_pcs, init, max_depth);
- ニューラルネットワークに対するAdversarial Exampleの生成
Python APIの少し面白い使い方としては、PyTorchやsklearnを用いて学習されたニューラルネットワークに対する敵対的サンプルを生成することができます。
from sklearn.neural_network import MLPClassifier
import pylibgymbo as plg
import pymlgymbo as pmg
clf = MLPClassifier(activation="relu")
clf.fit(X_train, y_train)
mlp_code = pmg.dump_sklearn_MLP(clf, feature_names)
adv_condition = (
"("
+ " || ".join(
[f"(y_{c} > y_{y_pred})" for c in range(len(clf.classes_)) if y_pred != c]
)
+ ")"
)
optimizer = plg.GDOptimizer(num_itrs, step_size, ...)
var_counter, prg = plg.gcompile(mlp_code)
executor = plg.SExecutor(optimizer, maxSAT, maxUNSAT, max_num_trials,
ignore_memory, use_dpll, verbose_level)
executor.run(prg, target_pcs, init, max_depth)
この手法の仕組みとしては、Gopinath, Divya, et al. "Symbolic execution for importance analysis and adversarial generation in neural networks." 2019 IEEE 30th International Symposium on Software Reliability Engineering (ISSRE). IEEE, 2019.を基に、ニューラルネットワークをImperativeなプログラムに変換した上で、Adversarial Exampleが満たすべき条件を論理式として記述するアプローチを採用しました。
5 感想
卒論の息抜きにとして勢いだけで作ったツールですが、ニューラルネットワークのデバックや、モンティホール問題の解決など、意外と色々な問題を解くことができて面白かったです。色々はしょり過ぎてかなり分かりにくい記事になってしまったので、時間がある時に加筆・修正しようと思います。