LoginSignup
2
2

More than 1 year has passed since last update.

@KouichiGodai(Araki Kouichi)in五大開発株式会社

傾斜量の算出方法（その２）

Posted at

前回に引き続き，今回も傾斜量の計算方法について紹介したいと思います．
前回は，傾斜量の計算方法を1つだけ紹介しましたが，傾斜量の計算方法は他にも提案されています．今回は，それらについて紹介します．前回と同様，Pythonのプログラムも掲載しています．

1．傾斜量の計算方法

今回は，以下の文献に記載されている計算方法で傾斜量を算出してみます．

  • 神谷泉，田中耕平，長谷川裕之，黒木貴一，早田 靖博，小田切聡子，政春尋志，"傾斜量図の作成とその応用"，情報地質，Vol.10，No.2，pp.76-79，1999年

  • 独立行政法人土木研究所　土砂管理研究グループ　地すべりチーム，地すべり地における航空レーザー測量データ解析マニュアル，土木研究所資料，平成21年6月

  • 戸田堅一郎，”安全な路網計画のための崩壊危険地ピンポイント抽出技術 -CS立体図を用いた崩壊危険地形判読技術の開発-”，長野県林業総合センター，32号，pp.1-16，2018年

2. 利用する標高データ

傾斜量の算出で入力となる標高データは，前回と同じGeoTIFFファイルです．このGeoTIFFファイルは，兵庫県が公開している1mピッチの標高データ（テキスト）をGeoTIFFファイルに変換したものです．

1mdem.jpg

3. 各計算方法による傾斜量の算出

3.1. 神谷らの計算方法

神谷らの論文に記載されている傾斜量の計算方法は，

Sx = \frac{Z_{i-1,j-1}+Z_{i-1,j}+Z_{i-1,j+1}-(Z_{i+1,j-1}+Z_{i+1,j}+Z_{i+1,j+1})}{6 \times \Delta x} \\
Sy = \frac{Z_{i-1,j-1}+Z_{i,j-1}+Z_{i+1,j-1}-(Z_{i-1,j+1}+Z_{i,j+1}+Z_{i+1,j+1})}{6 \times \Delta y} \\
Slop = \sqrt{Sx^2+Sy^2}

となっています．他の計算方法と比較するために，インデックスの記載方法とアルファベットが神谷らの論文とは異なっていますが，意味としては全く同じです．ここで，$Z$は標高値であり，$i$と$j$はそれぞれX方向とY方向のインデックスです．$\Delta x$と$\Delta y$は，それぞれX方向とY方向のデータの物理的距離の間隔を示しています．標高データのグリッドピッチは1mなので，$\Delta x=1$と$\Delta y=1$となります．この式から，傾斜量の計算対象セルに隣接する8セルを参照して，計算していることが分かります．

以下が，この計算方法をPyhonで記載したプログラムです．上式で算出される傾斜量は角度ではないため，プログラム上で角度に変換しています．

import argparse, math
import numpy as np
from osgeo import gdal, gdalconst

def main():
    ExeArgParser = argparse.ArgumentParser()
    ExeArgParser.add_argument('TiffPath', type=str)
    ExeArgParser.add_argument('OutputSlopPath', type=str)
    Args = ExeArgParser.parse_args()
    print(Args)

    # ndarray形式の標高とグリッドピッチの取得
    TiffData = gdal.Open(Args.TiffPath, gdalconst.GA_ReadOnly)
    Z = TiffData.GetRasterBand(1).ReadAsArray()
    GridPitch = abs(TiffData.GetGeoTransform()[1])
    print(Z.shape, GridPitch)

    # 傾斜量の算出
    SlopGrad = np.zeros(Z.shape)
    for IndexY in range(1, Z.shape[0]-1):
        for IndexX in range(1, Z.shape[1]-1):

            x = ((Z[IndexY-1, IndexX-1] + Z[IndexY, IndexX-1] + Z[IndexY+1, IndexX-1]) \
                    - (Z[IndexY-1, IndexX+1] + Z[IndexY, IndexX+1] + Z[IndexY+1, IndexX+1])) / (6 * GridPitch)
            y = ((Z[IndexY-1, IndexX-1] + Z[IndexY-1, IndexX] + Z[IndexY-1, IndexX+1]) \
                    - (Z[IndexY+1, IndexX-1] + Z[IndexY+1, IndexX] + Z[IndexY+1, IndexX+1])) / (6 * GridPitch)
            SlopGrad[IndexY, IndexX] = math.sqrt(x * x + y * y)

            # 角度に変換
            SlopGrad[IndexY, IndexX] = (360 / (2 * math.pi)) * math.atan(SlopGrad[IndexY, IndexX])

    # 四捨五入で，小数点以下2桁に丸める
    SlopGrad = np.round(SlopGrad, decimals=2)

    # TIFFとしてデータを保存
    Dtype, NumBand = gdal.GDT_Float32, 1
    OutputTif = gdal.GetDriverByName('GTiff').Create(Args.OutputSlopPath, SlopGrad.shape[1], SlopGrad.shape[0], NumBand, Dtype)
    OutputTif.SetGeoTransform(TiffData.GetGeoTransform()) # 座標系指定
    OutputTif.SetProjection(TiffData.GetProjection()) # 空間情報を結合
    OutputTif.GetRasterBand(1).WriteArray(SlopGrad) # 傾斜量を設定
    OutputTif.FlushCache() # ディスクに書き出し
    OutputTif = None

if __name__ == "__main__":
    main()

下図が，神谷らの計算方法で算出した傾斜量のGeoTIFFファイルをQGISで表示した傾斜量図になります．黒いほど傾斜がきつい（角度が大きい）部分になります．
slop_Kamiya.JPG

3.2. 土木研究所 地すべり地チームの計算方法

地すべりチームの文献に記載されている傾斜量の計算方法は，

Slop = \arctan \Biggl( \sqrt{\biggl(\frac{dz}{dx}\biggl)^2 + \biggl(\frac{dz}{dy}\biggl)^2} \Biggl) \times 57.29578\\
\frac{dz}{dx} = \frac{Z_{i-1,j-1}+2\times Z_{i-1,j}+Z_{i-1,j+1}-(Z_{i+1,j-1}+2\times Z_{i+1,j}+Z_{i+1,j+1})}{8 \times \Delta x} \\
\frac{dz}{dy} = \frac{Z_{i-1,j-1}+2\times Z_{i,j-1}+Z_{i+1,j-1}-(Z_{i-1,j+1}+2\times Z_{i,j+1}+Z_{i+1,j+1})}{8 \times \Delta y} \\

となっています．ここでも，数式の記載方法が文献とは異なっていますが，意味としては同じです．神谷らの計算方法と同様に，$Z$は標高値であり，$i$と$j$はそれぞれX方向とY方向のインデックスです．$\Delta x$と$\Delta y$は，それぞれX方向とY方向のデータの物理的距離の間隔を示しています．
地すべりチームの計算方法も，傾斜量の計算対象セルに隣接する8セルを参照して，計算しています．式中の57.29578は$\frac{360}{2\pi}$の計算結果であるため，$arctan$と組み合わせることで角度に変換しています．

以下が，この計算方法をPyhonで記載したプログラムです．

import argparse, math
import numpy as np
from osgeo import gdal, gdalconst

def main():
    ExeArgParser = argparse.ArgumentParser()
    ExeArgParser.add_argument('TiffPath', type=str)
    ExeArgParser.add_argument('OutputSlopPath', type=str)
    Args = ExeArgParser.parse_args()
    print(Args)

    # ndarray形式の標高とグリッドピッチの取得
    TiffData = gdal.Open(Args.TiffPath, gdalconst.GA_ReadOnly)
    Z = TiffData.GetRasterBand(1).ReadAsArray()
    GridPitch = abs(TiffData.GetGeoTransform()[1])
    print(Z.shape, GridPitch)

    # 傾斜量の算出
    SlopGrad = np.zeros(Z.shape)
    for IndexY in range(1, Z.shape[0]-1):
        for IndexX in range(1, Z.shape[1]-1):

            x = ((Z[IndexY-1, IndexX-1] + 2 * Z[IndexY, IndexX-1] + Z[IndexY+1, IndexX-1]) \
                    - (Z[IndexY-1, IndexX+1] + 2 * Z[IndexY, IndexX+1] + Z[IndexY+1, IndexX+1])) / (8 * GridPitch)
            y = ((Z[IndexY-1, IndexX-1] + 2 * Z[IndexY-1, IndexX] + Z[IndexY-1, IndexX+1]) \
                    - (Z[IndexY+1, IndexX-1] + 2 * Z[IndexY+1, IndexX] + Z[IndexY+1, IndexX+1])) / (8 * GridPitch)
            SlopGrad[IndexY, IndexX] = math.atan(math.sqrt(x * x + y * y)) * 57.29578

    # 四捨五入で，小数点以下2桁に丸める
    SlopGrad = np.round(SlopGrad, decimals=2)

    # TIFFとしてデータを保存
    Dtype, NumBand = gdal.GDT_Float32, 1
    OutputTif = gdal.GetDriverByName('GTiff').Create(Args.OutputSlopPath, SlopGrad.shape[1], SlopGrad.shape[0], NumBand, Dtype)
    OutputTif.SetGeoTransform(TiffData.GetGeoTransform()) # 座標系指定
    OutputTif.SetProjection(TiffData.GetProjection()) # 空間情報を結合
    OutputTif.GetRasterBand(1).WriteArray(SlopGrad) # 傾斜量を設定
    OutputTif.FlushCache() # ディスクに書き出し
    OutputTif = None

if __name__ == "__main__":
    main()

下図が，地すべりチームの計算方法で算出した傾斜量図になります．黒いほど傾斜がきつい（角度が大きい）部分になります．神谷らの結果と見た目はほぼ変わりありません．
slop_Doken.JPG

3.3. 戸田の計算方法

戸田の論文に記載されている傾斜量の計算方法は，

Slop = \arctan \Biggl( \sqrt{\biggl(\frac{dz}{dx}\biggl)^2 + \biggl(\frac{dz}{dy}\biggl)^2} \Biggl) \times \frac{180}{\pi}\\
\frac{dz}{dx} = \frac{(Z_{i+1,j-1}+2\times Z_{i+1,j}+Z_{i+1,j+1}) \times 4 - (Z_{i-1,j-1}+2\times Z_{i-1,j}+Z_{i-1,j+1}) \times 4}{8 \times \Delta x} \\
\frac{dz}{dy} = \frac{(Z_{i-1,j+1}+2\times Z_{i,j+1}+Z_{i+1,j+1}) \times 4 - (Z_{i-1,j-1}+2\times Z_{i,j-1}+Z_{i+1,j-1}) \times 4}{8 \times \Delta y}

となっています．ここでも，数式の記載方法が文献とは異なっていますが，意味としては同じです．これまでと同様に，$Z$は標高値であり，$i$と$j$はそれぞれX方向とY方向のインデックスです．$\Delta x$と$\Delta y$は，それぞれX方向とY方向のデータの物理的距離の間隔です．
戸田の計算方法も，傾斜量の計算対象セルに隣接する8セルを参照して，計算しています．地すべりチームの計算方法と比べると，重みの付け方に違いがあります．なお，この数式は，ArcGISから参照した式だそうです．

以下が，Pyhonで記載したプログラムです．

import argparse, math
import numpy as np
from osgeo import gdal, gdalconst

def main():
    ExeArgParser = argparse.ArgumentParser()
    ExeArgParser.add_argument('TiffPath', type=str)
    ExeArgParser.add_argument('OutputSlopPath', type=str)
    Args = ExeArgParser.parse_args()
    print(Args)

    # ndarray形式の標高とグリッドピッチの取得
    TiffData = gdal.Open(Args.TiffPath, gdalconst.GA_ReadOnly)
    Z = TiffData.GetRasterBand(1).ReadAsArray()
    GridPitch = abs(TiffData.GetGeoTransform()[1])
    print(Z.shape, GridPitch)

    # 傾斜量の算出
    SlopGrad = np.zeros(Z.shape)
    for IndexY in range(1, Z.shape[0]-1):
        for IndexX in range(1, Z.shape[1]-1):

            x = ((Z[IndexY-1, IndexX+1] + 2 * Z[IndexY, IndexX+1] + Z[IndexY+1, IndexX+1]) * 4 \
                    - (Z[IndexY-1, IndexX-1] + 2 * Z[IndexY, IndexX-1] + Z[IndexY+1, IndexX-1]) * 4) / (8 * GridPitch)
            y = ((Z[IndexY+1, IndexX-1] + 2 * Z[IndexY+1, IndexX] + Z[IndexY+1, IndexX+1]) * 4 \
                    - (Z[IndexY-1, IndexX-1] + 2 * Z[IndexY-1, IndexX] + Z[IndexY-1, IndexX+1]) * 4) / (8 * GridPitch)
            SlopGrad[IndexY, IndexX] = math.atan(math.sqrt(x * x + y * y)) * (180 / math.pi)

    # 四捨五入で，小数点以下2桁に丸める
    SlopGrad = np.round(SlopGrad, decimals=2)

    # TIFFとしてデータを保存
    Dtype, NumBand = gdal.GDT_Float32, 1
    OutputTif = gdal.GetDriverByName('GTiff').Create(Args.OutputSlopPath, SlopGrad.shape[1], SlopGrad.shape[0], NumBand, Dtype)
    OutputTif.SetGeoTransform(TiffData.GetGeoTransform()) # 座標系指定
    OutputTif.SetProjection(TiffData.GetProjection()) # 空間情報を結合
    OutputTif.GetRasterBand(1).WriteArray(SlopGrad) # 傾斜量を設定
    OutputTif.FlushCache() # ディスクに書き出し
    OutputTif = None

if __name__ == "__main__":
    main()

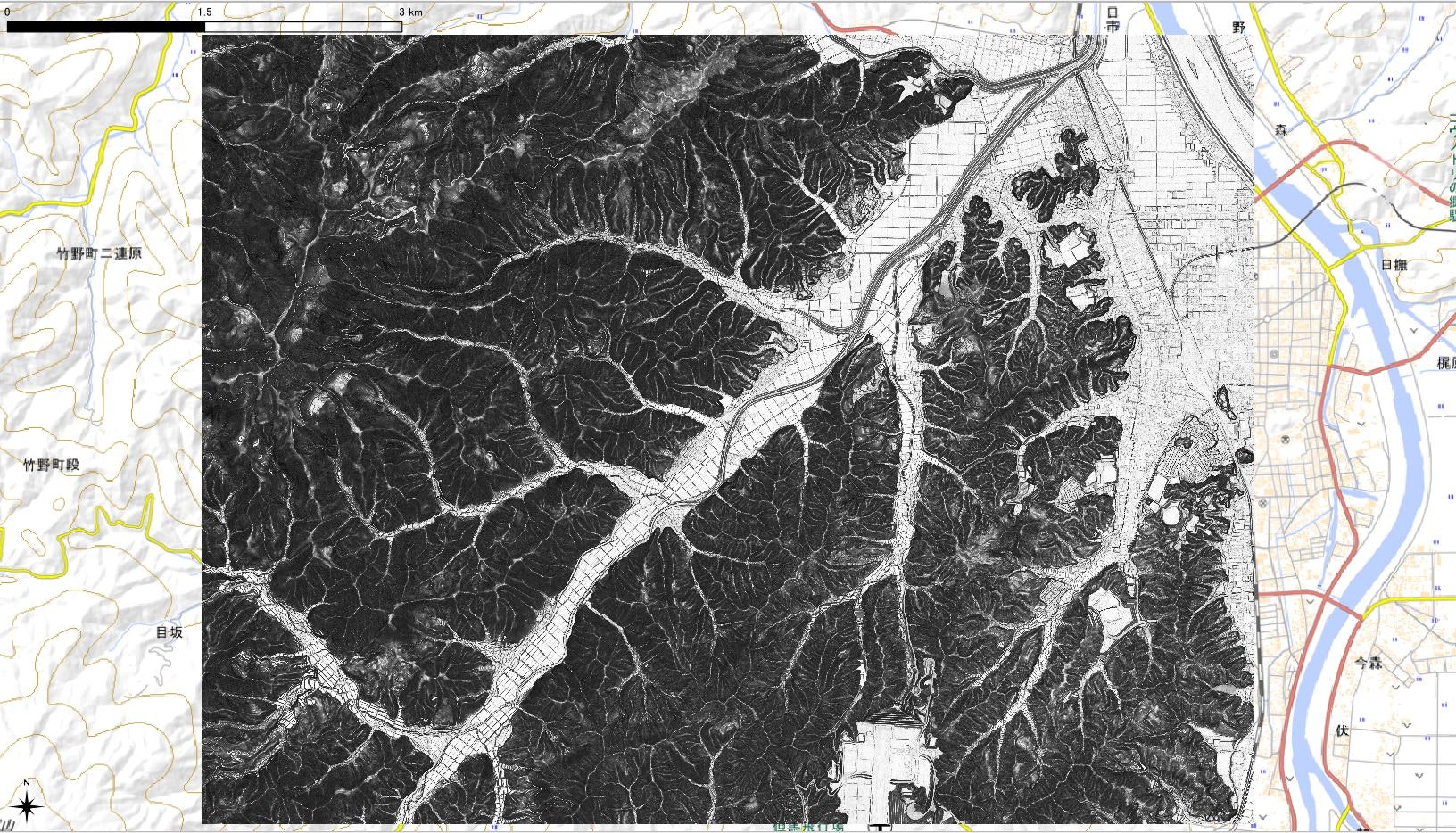
下図が，戸田の計算方法で算出した傾斜量図になります．これまでと同様に，黒いほど傾斜がきつい（角度が大きい）部分になります．前の2つの結果と比較すると，斜面部が濃くなっていますので，斜面を視覚的に強調するときには有効なのかもしれません．

slop_Toda.JPG

2
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
2