ただの集団 Advent Calendar 2018の25日目です。
n-gondo123さんのClickHouseの使い方とパーティションの話でした。
今回のアドベントカレンダーは自分がアンカーということなのですが、自由にやらせてもらうのでよろしくお願いします。
はじめに
年末に近づくにつれて自分は「またこの季節が来てしまったか。。。」と思うのです。
年末、つまりギャンブルの季節です!
年末ジャンボ等々の宝くじにはじまり、
競馬競輪競艇等の公営ギャンブルも栄え、
さらに年が明ければお年玉麻雀や家族ドンジャラで賑わう、
そんな季節じゃないでしょうか?
今回は特に競馬の市場について簡単な分析をし、無策でギャンブルに挑むことの危険性を説明していこうかなと思います。
注意事項
- 難しい分析や機械学習のロジックについて話しません。今回は
行動経済学的なアプローチです。 - 馬の強さについては話しません。今回は行動経済学的な市場の話です。
今回使う用語の説明
本命-大穴バイアス
今回の分析の本題。
「1着になる確率は低いがオッズの高い大穴馬券は,客観的な勝利確率よりも過剰に人気があり、
一方、1着になる確率は高いがオッズの低い本命馬券は,実際の客観確率よりも人気が低い傾向を指す。」(「競馬とプロスペクト理論」より)
要は人は一攫千金を求めて強くない馬に過剰に投資するみたいなこと
ロジスティック回帰
被説明変数が2値の時に使う回帰モデルの一つ。
y = 1 / (1 + e^-(ax + b))
のような回帰式になる。
データの収集
stockedgeさんのnetkeiba-scraperを使わせてもらいます。そのままだと動かないので修正が必要ですが、今回の本題とは離れるので時間があったらあとで追記します。
分析
今回の分析では以下の値を扱います。
被説明変数: 馬が1位になったかどうか(1/0)
説明変数: オッズの逆数(全体の何%の金額がその馬に投資したのか)
こんな感じのデータを読み込ませて分析してみます。
isWin odds rate
0 0 119.9 0.008340
1 0 60.8 0.016447
2 1 2.8 0.357143
3 0 10.9 0.091743
4 0 10.2 0.098039
5 0 312.8 0.003197
1行1行はそれぞれ、レースで走る馬のオッズと、その馬が1位になったかどうかです。
rateに関しては1/oddsで擬似的にその馬への投資割合を出しています。
それでは実際に分析していくと、
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
datas = pd.read_csv('inputData.csv')
y_datas = pd.DataFrame(datas['isWin'], columns=['isWin']).values
x_datas = pd.DataFrame(datas['rate'], columns=['rate']).values
# 適当にデータを分割しておきます。
n_train_rate = 0.7
train_x_data, test_x_data, train_y_data, test_y_data = train_test_split(x_datas, y_datas, test_size=1-n_train_rate)
lr = LogisticRegression()
lr.fit(train_x_data, train_y_data)
a = lr.coef_
b = lr.intercept_
ここ出てくるa, bが上に書いた回帰モデルのa, bにあたるものです。
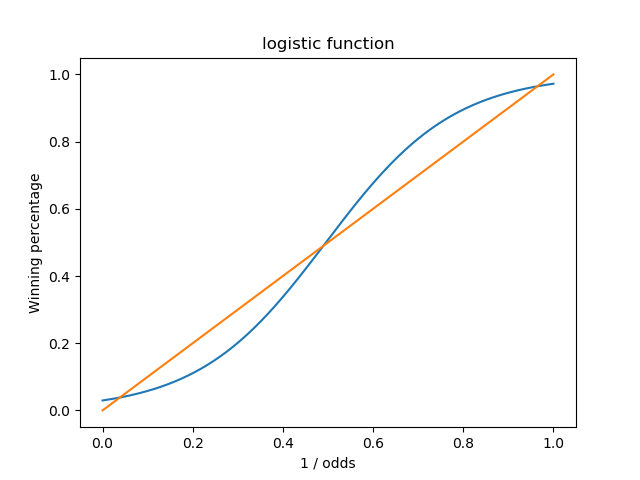
グラフにするとこんな感じ。
横軸が全体の何%の金額がその馬に投資されたのか、縦軸がその投資割合に対する勝率です。
青い線がロジスティック回帰の結果で、赤い線が投資割合と勝率が一致するラインです。
大雑把にいうと青い線が赤い線より上にある部分が回収金額の期待値がプラスになるところになります。
例えば、投資割合が0.2の馬がいたとした時、その馬は0.2どころか0.1の確率でも勝っていないと思われます。
投資割合が0.2の馬の場合、オッズはだいたい5倍くらいになるので、
回収金額の期待値的には0.5となり、マイナスになってしまいます。
このマイナスになってしまう部分がタイトルにあるような「本命-大穴バイアス」にあたります。
実践
せっかく分析したのだから、実際にシミュレートしてみないといけないような気がします。
先ほどの分析時にデータを二つに分けていたので、使っていない方を用いて検証してみます。
競馬では1着かどうかを知りたい、というよりは期待値でプラスのリターンが見込めるものを見出したいです。!
まずはシンプルに0/1の予測値に基づいて投資してみる
predict_df = pd.concat([pd.DataFrame(lr.predict(test_x_data), columns=['predictions']),
pd.DataFrame(test_odds_data, columns=['odds']).reset_index(),
pd.DataFrame(test_y_data, columns=['isWin']).reset_index()], axis=1)
predict_df['invest'] = predict_df['predictions'] * 100
predict_df['return'] = predict_df['odds'] * predict_df['isWin'] * predict_df['invest'] - predict_df['invest']
print(predict_df.sum())
予測値が1の馬全てに100円ずつ投資してみるとします。
今回は作ったモデルのアウトプットが0/1なのでpredictを使います。
このような形で出力するとこんな結果が出てきます。
結果
[13380 rows x 7 columns]
predictions 237.0
odds 925675.6
isWin 956.0
invest 23700.0
return -4620.0
勝てないやん。。。
1になる確率 × oddsが1を超えるものに投資してみる
predict_df = pd.concat([pd.DataFrame(test_odds_data, columns=['odds']).reset_index(),
pd.DataFrame(test_y_data, columns=['isWin']).reset_index()], axis=1)
predict_df['prediction'] = lr.predict_proba(test_x_data)[:, 1]
predict_df['invest'] = 0
predict_df.loc[predict_df['prediction'] * predict_df['odds'] > 1, 'invest'] = 100
predict_df['return'] = predict_df['odds'] * predict_df['isWin'] * predict_df['invest'] - predict_df['invest']
続いて、先ほどとは別に作成したモデルのアウトプットが1になる確率とオッズからリターンの期待値を出して投資してみます。
[13380 rows x 7 columns]
odds 9.428121e+05
isWin 9.870000e+02
prediction 9.486751e+02
invest 6.568000e+05
return -2.403900e+05
やっぱり勝てないやん。。。
終わりに
本当はログ基盤についてAWSとGCPの良いとこどりをしたようなものを書こうかなーと思っていたのですがそちらは時間が足らず。。。
今回は大学時代に研究していたテーマをプログラムにしてみた(導入編)みたいなものを書いてみました。
大学時代は収支がプラスになっていたはずなのにおかしい。。。
行動経済学的にはギャンブル市場はとても良い市場だと言われています。
というのも、純粋な利害関係しか存在しないため、人間の行動性質が如実に現れるためです。
今回はオッズと実際の勝率という簡単なモデルで分析してみてもこのような結果になるので、
他にもダミー変数を入れてみたらより面白い結果になるかもしれません。
また機会があれば今度はそれを逆手に取ったギャンブルでの投資方法などを書いてみようかなと思います。
ではでは良いクリスマスを!