動機
機械学習関連の知識を再確認していて、まずは最も基本的な手法、k-NN法(k最近傍法)を勉強がてら自前で実装してみました。
k-NN法とは
まずはk-NNの概要からおさらいします。とてもシンプルでわかりやすいアルゴリズムなのですぐ理解できると思います。
このアルゴリズムは下の図が全てです。
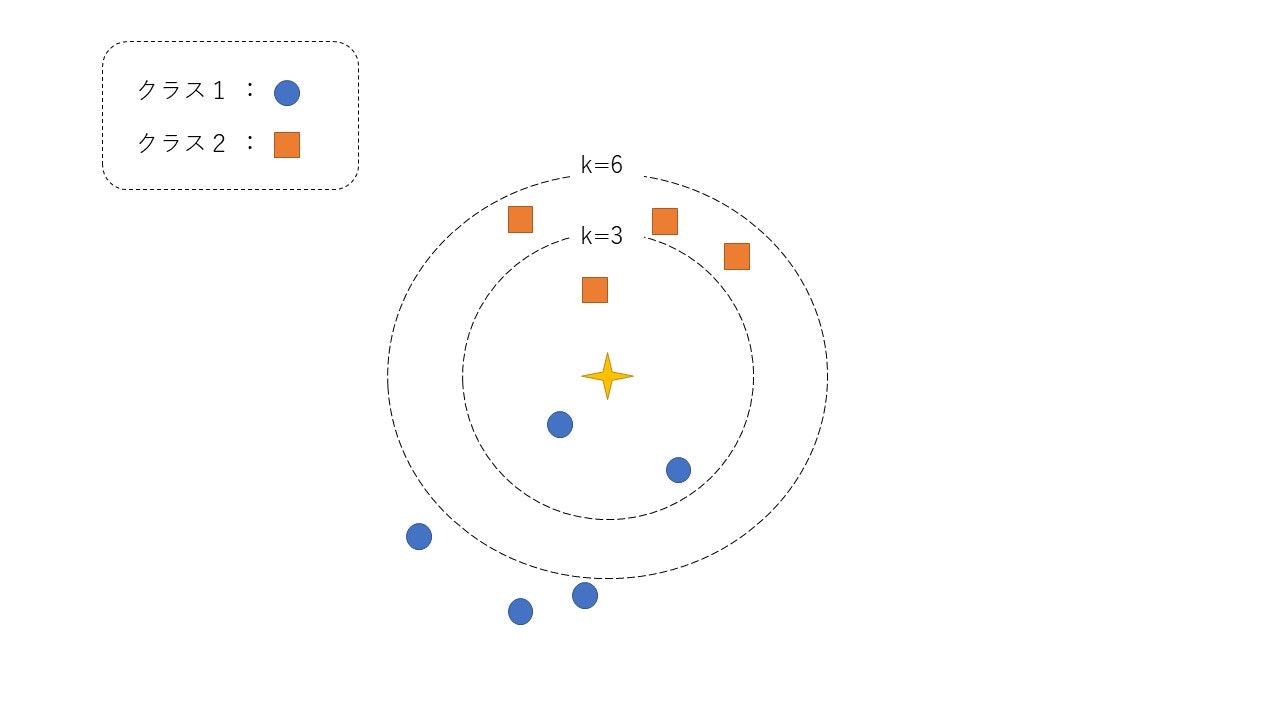
注目データは中心の星印です。まず与えられたデータに対して全てのデータ間の距離を計算します。例えばk=3のとき、注目データに最も近い上位3個のデータのラベルを見ます。この場合、クラス1が2個、クラス2は1個なので最頻値を取るクラス1に分類されます。一方で、k=6としてみると、クラス1が2個、クラス2が6個となるので、このデータはクラス2に分類されます。
このように与えられたデータは近いデータのラベルの多数決で決定されることになります。
ちなみにk=1のときは最近傍法とも呼ばます。
似たような名前の手法にk-means法がありますが、これは教師なしのクラスタリングの手法で、教師付き分類手法であるk-NN法とは異なった手法です。
実装
それでは実際にPythonで実装していきたいと思います。
データセット
データセットは有名なIris Data Setを使います。
ますiris.dataをダウンロードして実際にデータを読み込みます。
data = np.loadtxt('iris.data', delimiter=',', dtype='float64',usecols=[0, 1, 2, 3])
labels = np.loadtxt('iris.data', delimiter=',', dtype='str',usecols=[4])
print(data.shape)
print(labels.shape)
(150, 4)
(150,)
このデータセットは4つの特徴量を持つ150個のデータとそのラベル(3クラス)で構成されています。
最近傍探索
今回はこれらのライブラリを使います。
import numpy as np
from sklearn import model_selection
from scipy.spatial import distance
from sklearn.metrics import accuracy_score
from statistics import mean, median,variance
まずは与えられた点に対して各データとの距離を計算します。
distance_matrix = distance.cdist(test_data, train_data)
indexes = np.argsort(distance_matrix, axis=1)
次に与えられたデータの近傍k個のデータに対して、どのクラスのデータが何個あるのか数えます。
class_dict = {}
for label in labels:
class_dict[label] = 0
class_dict_list = []
for data_num, index in enumerate(indexes[:,:self.k]):
class_dict_list.append(class_dict.copy())
for i in index:
class_dict_list[data_num][self._labels[i]] += 1
最後に最も多かったクラスのラベルを特定します。
predict_class = []
for d in class_dict_list:
max_class = max(d, key=d.get)
predict_class.append(max_class)
k-NNアルゴリズム自体はこれで全部です。
実行
今回は各クラスをランダムに半分に分けて、学習、実行の流れを20回繰り返します。実際の実行結果は以下のようになります。(ランダムにデータを分けるので、精度に多少の差は出ます。)
training number 1 ...
knn accuracy : 0.9466666666666667
training number 2 ...
knn accuracy : 0.9333333333333333
training number 3 ...
knn accuracy : 0.9466666666666667
training number 4 ...
knn accuracy : 0.9466666666666667
training number 5 ...
knn accuracy : 0.9333333333333333
training number 6 ...
knn accuracy : 0.92
training number 7 ...
knn accuracy : 0.9466666666666667
training number 8 ...
knn accuracy : 0.9466666666666667
training number 9 ...
knn accuracy : 0.8933333333333333
training number 10 ...
knn accuracy : 0.9466666666666667
training number 11 ...
knn accuracy : 0.96
training number 12 ...
knn accuracy : 0.96
training number 13 ...
knn accuracy : 0.96
training number 14 ...
knn accuracy : 0.96
training number 15 ...
knn accuracy : 0.92
training number 16 ...
knn accuracy : 0.96
training number 17 ...
knn accuracy : 0.92
training number 18 ...
knn accuracy : 0.9866666666666667
training number 19 ...
knn accuracy : 0.9333333333333333
training number 20 ...
knn accuracy : 0.96
=================================================
knn accuracy mean : 0.944
knn accuracy variance : 0.00042292397660818664
このように、高い精度が実現できているのがわかると思います。
感想
シンプルなアルゴリズムだけあって非常に簡単に実装できました。今回のデータのように次元が小さく、少ないデータ数ならば非常に効果的です。
しかし、実際には高次元データに対して次元の呪いの効果でユークリッド距離が意味をなさなくなったり、大規模データセットでは時間計算量、空間計算量ともに実用的ではありません。
このような問題にはベクトルをハッシュ化したり、量子化したりする手法によって、メモリ消費量や計算量を削減する方法が提案されています。
実際のソースコードはgithub上で確認できます。
https://github.com/kotaYkw/machine_learning