記事の概要
個人的な勉強メモです。
コンピュータの構成と設計第6版の5章の演習問題を解いてみました。
自分なりに考えた解答なので、間違いや誤答も多くあると思います。
ネットの情報を参照してなるべく間違いがないように努めていますが、本記事の解答をあまり信用しないようご注意ください。
5.1
5.1.1
キャッシュは複数のキャッシュラインから構成されています。
キャッシュラインとはデータとタグのペアです。
データがnバイトのキャッシュラインにはmビットの値が$n/(m/8)$個格納できます。
よって本問の答えは4です。
5.1.2
短い時間内に多く参照される変数は時間局所性があると言えます。
本問では、数式において各変数がどれだけ参照されているかに注目します。
forループの局所変数であるIとJは、変数の値を更新させながら1ループ当たり8,000回参照されています。
またB[I][0]も各Iに対して、1ループ当たり8,000回参照されています。
A[I][J]とA[J][I]は、異なるIやJならば異なる変数なので、1ループ当たり1回ずつしか参照されていません。
よって答えはIとJとB[I][0]です。
5.1.3
参照される変数の内、アドレスが近い変数は空間局所性があると言えます。
A[I][J]のアドレスはA[I][0]のアドレス+Jなので、forループでJが0から8000まで連続しており、空間局所性があります。
一方でA[J][I]のアドレスはA[J][0]のアドレス+Iなので、forループではJについてアドレスが連続しておらず、空間局所性はありません。
また、B[I][0]のアドレスはB[I][0]のアドレス+0なので、forループではIについてアドレスが連続しておらず、空間局所性はありません。
よって答えはA[I][J]です
5.1.4
まずforループで行列要素が参照される回数を求めます。
A[I][J]が8×8,000回、A[J][I]が8×8,000回参照されます。ただしI=Jとなるアドレスが重複する8×8=64回を除きます。
B[I][0]が8,000回参照されます。
キャッシュラインあたり32ビット=4バイトなので、(8000×2-64+8000)/4 = 33,984個のキャッシュラインがあれば、参照される全ての行列要素を格納できます。
5.1.5
MATLABでも短い時間で繰り返し参照される変数は変わりません。
よって答えはIとJとB[I][0]です。
5.1.6
Cでは同じ行内の行列要素が連続していましたが、MATLABでは同じ列内の行列要素が連続しています。
つまりA[I][J]のアドレスはA[0][J]のアドレス+Iなので、forループではJについてアドレスが連続しておらず、空間局所性はありません。
一方でA[J][I]のアドレスはA[0][I]のアドレス+Jなので、forループでJが0から8000まで連続しており、空間局所性があります。
また、B[I][0]のアドレスはB[0][0]のアドレス+Iなので、forループでIが0から8まで連続しており、空間局所性があります。
よって答えはA[J][I]とB[I][0]です
5.2
5.2.1
ダイレクトマップ方式とは、あるアドレスのデータをキャッシュに格納する際、キャッシュの格納場所が決まっています。
その場所をインデックスと呼び、インデックスは(アドレス%キャッシュのブロック数)になります。
アドレスの下位部分であるインデックスを除いた上位アドレスはタグと呼ばれます。
キャッシュのタグとインデックスを参照することで、メインメモリのアドレスを一意的に特定できます。
本問ではブロック数が16なので各アドレスのインデックスは下位4ビット、タグは上位4ビットになります。
タグかインデックスのどちらかが初出ですとキャッシュ・ミスになります。よって本問では全てがキャッシュ・ミスになります。
| 16進アドレス | 2進アドレス | タグ | インデックス | ヒット |
|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x0 | 0x3 | ミス |
| 0xb4 | 1011 0100 | 0xb | 0x4 | ミス |
| 0x2b | 0010 1011 | 0x2 | 0xb | ミス |
| 0x02 | 0000 0010 | 0x0 | 0x2 | ミス |
| 0xbf | 1011 1111 | 0xb | 0xf | ミス |
| 0x58 | 0101 1000 | 0x5 | 0x8 | ミス |
| 0xbe | 1011 1110 | 0x5 | 0xe | ミス |
| 0x0e | 0000 1110 | 0x0 | 0xe | ミス |
| 0xb5 | 1011 0101 | 0xb | 0x5 | ミス |
| 0x2c | 0010 1100 | 0x2 | 0xc | ミス |
| 0xba | 1011 1010 | 0xb | 0xa | ミス |
| 0xfd | 1111 1101 | 0xf | 0xd | ミス |
本問の例ですと、0xbeと0x0eは同じインデックス0xeに格納されます。
よって0xbeの次に0x0eが来た時には、0xbeを0x0eで上書きして、タグを0xbから0x0に更新しないといけません。
5.2.2
キャッシュラインの1語のデータ・サイズが$n = 2^k$バイトの場合は、アドレスの下位kビットは語内のバイト・オフセットとしてアドレスから除外します。(本問では語内のバイト・オフセットは織り込み済みとみなします。)
また、キャッシュラインの語が$m = 2^l$個の場合は、アドレスの下位kビットはアドレスから除外します。
この時、必要なブロック数は「キャッシュデータサイズ$/2^{k+l}$」になります。
例えば、5.2.1はデータ・サイズが1語だったので、アドレスの0x02と0x03は区別しないといけません。
ですが、今回はデータ・サイズが2語なので、最下位1ビットを無視するので、アドレスの0x02=0b10と0x03=0b11は同じインデックス0b1に属します。
キャッシュデータサイズは前問と同じでも、2語になったことでブロック数は前問の半分の8個になり、インデックスは下位3ビットのみになります。
ただし最下位1ビットを無視した上での下位3ビットadress[3:1]です。
よってタグはインデックスを除いたアドレスなので、上位4ビット、address[7:4]のままです。
今回の場合は、同じタグとインデックスの組み合わを参照してキャッシュがヒットする場合が2回あります。
| 16進アドレス | 2進アドレス | タグ | インデックス | ヒット |
|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x0 | 0x1 | ミス |
| 0xb4 | 1011 0100 | 0xb | 0x2 | ミス |
| 0x2b | 0010 1011 | 0x2 | 0x5 | ミス |
| 0x02 | 0000 0010 | 0x0 | 0x1 | ヒット |
| 0xbf | 1011 1111 | 0xb | 0x7 | ミス |
| 0x58 | 0101 1000 | 0x5 | 0x4 | ミス |
| 0xbe | 1011 1110 | 0x5 | 0x7 | ミス |
| 0x0e | 0000 1110 | 0x0 | 0x7 | ミス |
| 0xb5 | 1011 0101 | 0xb | 0x2 | ヒット |
| 0x2c | 0010 1100 | 0x2 | 0x6 | ミス |
| 0xba | 1011 1010 | 0xb | 0x5 | ミス |
| 0xfd | 1111 1101 | 0xf | 0x6 | ミス |
5.2.3
8語のデータを収められる場合のC1、C2、C3のブロック数とオフセット、インデックスのビット範囲は以下になります。
| パターン | ブロック・サイズ | ブロック数 | オフセット | インデックス |
|---|---|---|---|---|
| C1 | 1 | 8 | 0 | 下位3ビット |
| C2 | 2 | 4 | 1 | 下位2ビット |
| C3 | 4 | 2 | 2 | 下位1ビット |
C1の場合
| 16進アドレス | 2進アドレス | タグ | インデックス | ヒット |
|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x00 | 0x3 | ミス |
| 0xb4 | 1011 0100 | 0x16 | 0x4 | ミス |
| 0x2b | 0010 1011 | 0x05 | 0x3 | ミス |
| 0x02 | 0000 0010 | 0x00 | 0x2 | ミス |
| 0xbf | 1011 1111 | 0x17 | 0x7 | ミス |
| 0x58 | 0101 1000 | 0x0b | 0x0 | ミス |
| 0xbe | 1011 1110 | 0x17 | 0x6 | ミス |
| 0x0e | 0000 1110 | 0x01 | 0x6 | ミス |
| 0xb5 | 1011 0101 | 0x16 | 0x5 | ミス |
| 0x2c | 0010 1100 | 0x05 | 0x4 | ミス |
| 0xba | 1011 1010 | 0x17 | 0x2 | ミス |
| 0xfd | 1111 1101 | 0x1f | 0x5 | ミス |
ミス率は100%です。
C2の場合
インデックスは、オフセット最下位1ビットを除く、下位2ビットです。
よってタグはアドレス上位5ビットのままなのでC1と同じです。
| 16進アドレス | 2進アドレス | タグ | インデックス | ヒット |
|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x00 | 0x1 | ミス |
| 0xb4 | 1011 0100 | 0x16 | 0x2 | ミス |
| 0x2b | 0010 1011 | 0x05 | 0x1 | ミス |
| 0x02 | 0000 0010 | 0x00 | 0x1 | ミス |
| 0xbf | 1011 1111 | 0x17 | 0x3 | ミス |
| 0x58 | 0101 1000 | 0x0b | 0x0 | ミス |
| 0xbe | 1011 1110 | 0x17 | 0x3 | ヒット |
| 0x0e | 0000 1110 | 0x01 | 0x3 | ミス |
| 0xb5 | 1011 0101 | 0x16 | 0x2 | ヒット |
| 0x2c | 0010 1100 | 0x05 | 0x2 | ミス |
| 0xba | 1011 1010 | 0x17 | 0x1 | ミス |
| 0xfd | 1111 1101 | 0x1f | 0x2 | ミス |
0x03と0x02のインデックスとタグは一致していますが、0x02がミスになっているのは、0x02を参照する前に0x2bを参照した時にデータの置き換えをしているからです。
ミス率は10/12=83%です。
C3の場合
インデックスは、オフセット最下位2ビットを除く、下位1ビットです。
よってタグはアドレス上位5ビットのままなのでC1と同じです。
| 16進アドレス | 2進アドレス | タグ | インデックス | ヒット |
|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x00 | 0x0 | ミス |
| 0xb4 | 1011 0100 | 0x16 | 0x1 | ミス |
| 0x2b | 0010 1011 | 0x05 | 0x0 | ミス |
| 0x02 | 0000 0010 | 0x00 | 0x0 | ミス |
| 0xbf | 1011 1111 | 0x17 | 0x1 | ミス |
| 0x58 | 0101 1000 | 0x0b | 0x0 | ミス |
| 0xbe | 1011 1110 | 0x17 | 0x1 | ヒット |
| 0x0e | 0000 1110 | 0x01 | 0x1 | ミス |
| 0xb5 | 1011 0101 | 0x16 | 0x1 | ミス |
| 0x2c | 0010 1100 | 0x05 | 0x1 | ミス |
| 0xba | 1011 1010 | 0x17 | 0x0 | ミス |
| 0xfd | 1111 1101 | 0x1f | 0x1 | ミス |
ミス率は11/12=92%です。
どれが1番効率的か?
本問の答えは、参照回数、アクセス時間、ミスペナルティ時間により異なります。
誤植だと思いますが、問題文中にこれらの数字がないので答えは出せません。
参照回数を$n$、アクセス時間を$a_i$[cycle]$(i=1, 2 ,3)$、ミス率を$p_i$[%]$(i=1, 2 ,3)$、ミスペナルティ時間を$m_i$[cycle]$(i=1, 2 ,3)$として、$na_i + nm_i*p_i/100$が最小になるパターンが、最も効率的になります。
5.3
5.3.1
1語のデータサイズが64ビットなので、1ブロックのデータ2語は16バイトです。
32KiBのキャッシュは32×1024バイト/16バイト=2048個のブロック数を持ちます。
1語のデータサイズが64ビット=8バイト=$2^3$バイトなので、語内のバイト・オフセットは3ビットです。
1ブロックは2語から成るので、ブロック・サイズのオフセットは1ビットです。
インデックスは、アドレス0xFFFF % ブロック数2048 = $2^{11}$なので、アドレスの最下位のビット桁をオフセット分除いた、アドレスの下位11ビットです。
タグはオフセットとインデックスのビットを除いた、アドレスの上位(64-3-1-11)=49ビットです。
1つのブロックあたり、2語×64ビットのデータと49ビットのタグと1ビットの判定ビットを持ちます。
キャッシュは2048個のブロック数を持つので、総ビット数は$2048*(2*64+49+1)=364,544$ビットです。
5.3.2
1語のデータサイズが64ビットなので、1ブロックのデータ16語は128バイトです。
64KiBのキャッシュは64×1024バイト/128バイト=512個のブロック数を持ちます。
1語のデータサイズが64ビット=8バイト=$2^3$バイトなので、語内のバイト・オフセットは3ビットです。
1ブロックは16=$2^4$語から成るので、ブロック・サイズのオフセットは4ビットです。
インデックスは、アドレス0xFFFF % ブロック数511 = $2^9$なので、アドレスの最下位のビット桁をオフセット分除いた、アドレスの下位9ビットです。
タグはオフセットとインデックスのビットを除いた、アドレスの上位(64-3-4-9)=48ビットです。
1つのブロックあたり、16語×64ビットのデータと48ビットのタグと1ビットの判定ビットを持ちます。
キャッシュは512個のブロック数を持つので、総ビット数は$512*(16*64+48+1)=549,376$ビットです。
5.3.3
5.3.2のキャッシュは1ブロックのデータ・サイズが5.3.1より大きいですが、性能が落ちる可能性があります。
まず、データサイズが大きいとブロック数が減る為、頻繁にインデックスの重複によるキャッシュ・ミスが発生する恐れがあります。
更にデータサイズが大きいとキャッシュ・ミス時のデータ転送時間が増えます。
キャッシュ・ミスの増加とキャッシュ・ミスによるペナルティ時間の増加により、データ・サイズが大きくなると逆にキャッシュ性能が落ちる恐れがあります。
5.3.4
2ウェイ・セット・アソシアティブ方式は同じインデックスを2個まで保持できます。
これにより、インデックスの重複によるキャッシュ・ミスの発生確率を減らすことができます。
例えばアドレスの下位11ビットが同じ0x000007FFと0xFFFFFFF7FFは同じインデックスに属します。
参照するアドレスが0x000007FF→0xFFFFFFF7FF→0x000007FF→0xFFFFFFF7FF→0x000007FF→0xFFFFFFF7FFの繰り返しだった場合、最初の場合は全てミスになります。
ですが2ウェイ・セット・アソシアティブ方式ならば、2つまでインデックスを保持できるので、(初回参照時のミスを除いて)全てヒットになります。
5.4
(解答が正しいか自信のない問題)
話を簡単にする為に4ビットのアドレスの場合を考えます。
インデックスを「アドレス[3] XOR アドレス[2] 」とします。
同じインデックスを持つ異なるアドレスを識別する為には、例えばタグを以下のようにします。
このタグとインデックスから一意的なアドレスを逆算すれば、ダイレクト・マップ方式のインデックスを算出できます。
| 2進アドレス | タグ | インデックス |
|---|---|---|
| 0000 | 000 | 0 |
| 0001 | 001 | 0 |
| 0010 | 010 | 0 |
| 0011 | 011 | 0 |
| 0100 | 100 | 1 |
| 0101 | 101 | 1 |
| 0110 | 110 | 1 |
| 0111 | 111 | 1 |
| 1000 | 000 | 1 |
| 1001 | 001 | 1 |
| 1010 | 010 | 1 |
| 1011 | 011 | 1 |
| 1100 | 100 | 0 |
| 1101 | 101 | 0 |
| 1110 | 110 | 0 |
| 1111 | 111 | 0 |
この方式では、タグの数が8個必要になります。
もしインデックスを下位2ビットにすれば、タグは上位2ビットなので、タグの数は4個で済みます。
タグの数が多くなれば、インデックスの重複によるキャッシュ・ミスの発生確率も増えてしまいます。
よって、この方式を採用する利点があるとは思えません。
問題文のようにアドレスの桁数が増えても、同様のことが発生すると予測されます。
5.5
5.5.1
1語を$8=2^3$バイトとすれば、語内のバイト・オフセットは3です。
オフセットの総数が5なので、ブロック・サイズのオフセットは$5-3=2$です。
よってブロックの語数は$2^2=4$語となります。
5.5.2
キャッシュのエントリ数はインデックスの総数です。
インデックスは5ビットなので$2^5=32$個となります。
5.5.3
キャッシュライン1つあたりのデータ・サイズは4語×8バイト×8ビットなので、キャッシュ全体では32個×4語×8バイト×8ビット=8192ビットが必要になります。
キャッシュライン1つあたりのタグ・サイズは22ビット、判定ビットは1ビットなので、キャッシュ全体では32個×(22+1)ビット=736ビットが必要になります。
よってキャッシュ全体で必要なビット数とデータ部分のビット数の比は$8192:8192+736=1:1.09$となります。
5.5.4
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | 置き換えデータ |
|---|---|---|---|---|---|---|
| 0x000 | 0000 0000 0000 | 0x00 | 0x00 | 0 0000 | ミス | |
| 0x004 | 0000 0000 0100 | 0x00 | 0x00 | 0 0100 | ヒット | |
| 0x010 | 0000 0001 0000 | 0x00 | 0x00 | 1 0000 | ヒット | |
| 0x084 | 0000 1000 0100 | 0x00 | 0x04 | 0 0100 | ミス | |
| 0x0e8 | 0000 1110 1000 | 0x00 | 0x07 | 0 1000 | ミス | |
| 0x0a0 | 0000 1010 0000 | 0x00 | 0x05 | 0 0000 | ミス | |
| 0x400 | 0100 0000 0000 | 0x01 | 0x00 | 0 0000 | ミス | 0x000-0x01f |
| 0x01e | 0000 0001 1110 | 0x00 | 0x00 | 1 1110 | ミス | 0x400-0x41f |
| 0x08c | 0000 1000 1100 | 0x00 | 0x04 | 1 0000 | ヒット | |
| 0xc1c | 1100 0001 1100 | 0x03 | 0x00 | 1 1100 | ミス | 0x000-0x01f |
| 0x0b4 | 0000 1011 0100 | 0x00 | 0x05 | 1 0100 | ヒット | |
| 0x884 | 1000 1000 0100 | 0x02 | 0x04 | 0 0100 | ミス | 0x080-0x09f |
置き換えデータは直前に参照した同じインデックスを持つデータです。
置き換えるデータの範囲はオフセットの0x1fです。
(ちなみに、このブロックのデータサイズが大きいと、置き換えるのに時間がかかってしまいます。)
5.5.5
ヒット率は4/12=33%です。
5.5.6
キャッシュの最終状態を求めるには、最後に参照したインデックスを抜き出します。
| データ | タグ | インデックス |
|---|---|---|
| 0xc00-0xc1f | 0x03 | 0x00 |
| 0x880-0x91f | 0x02 | 0x04 |
| 0x0a0-0x0bf | 0x00 | 0x05 |
| 0x0e0-0x0ff | 0x00 | 0x07 |
5.6
5.6.1
ライトスルー方式は、ストア命令によりあるアドレスのデータを更新する際、更新データをキャッシュの該当アドレスに書き込むと同時に、主記憶の該当アドレスにも書き込みます。
ライトバック方式は、あるアドレスのデータを更新する際、更新データをキャッシュの該当アドレスに書き込みますが、主記憶の該当アドレスには書き込みません。
キャッシュラインが満杯になった時に、まとめて主記憶に書き込みます。
また、書き込み時に、キャッシュメモリに対応ブロックがなく、キャッシュミスした場合、以下の2通りの方式があります。
対応ブロックを主記憶から読み出してキャッシュに割り当て、このキャッシュブロックに書き込むのをライト・アロケート方式と呼びます。
主記憶から対応ブロックを読み出してキャッシュに格納することなく、主記憶にだけ書き込むのをノーライト・アロケート方式と呼びます
つまり、4つの組み合わせがあり得ます
- ライトスルー方式、かつライト・アロケート方式
- ライトスルー方式、かつノーライト・アロケート方式
- ライトバック方式、かつライト・アロケート方式
- ライトバック方式、かつノーライト・アロケート方式
そういえば、Cortex-M7のキャッシュにエラッタのあることが、以前に話題になったのを思い出します。
ライトスル―方式を用いて、同じアドレスに8バイトの読み書きをすると、データを正しく読みだせない事があるというものでした。
1次キャッシュはミス率を減らすよりも、ヒット時間を短くするように速度を重視します。
2次キャッシュは、ミスペナルティが大きい主記憶へのアクセスを減らすため、ミス率を減らすことを優先すします。
ミス率を減らすために2次キャッシュのサイズは1次キャッシより大きくなります。
以上のことを踏まえた上で、必要になるバッファについて検討します。
L1のライトスルー方式は、キャッシミス時に、常に主記憶にも書き込むのでミスペナルティ時間が大きくなります。
そこで、ライトバッファを用います。
ライトバッファに主記憶に書き込むデータを一時保存し、別途ライトバッファのデータを主記憶に書き込みます。
L2のライトバック方式はの場合は、データをライトバッファに一時保存して、キャッシュに上書きします。
5.6.2と5.6.3
(解答が正しいか自信のない問題)
問題を5.6.2と5.6.3を分けている意味がよく分かりませんでした。
どちらも同じことを聞いているように思えます。
L1キャッシュで書き込みミスがあると、次はL2キャッシュに書き込もうとします。
L1キャッシュはノーライト・アロケート方式なので、キャッシュに該当ブロックは格納しません。
L2キャッシュでも書き込みミスになれば、主記憶から該当ブロックが読みだされ、L2キャッシュにも該当ブロックが格納されます。
5.7
5.7.1
CPIが2なので、1サイクルあたり0.5命令があります。
命令キャッシュのミス率は0.3%で、ミスするごとに1ブロック64バイトが呼び出されるので、1サイクルあたりに読み出されるバイト数は$0.50.00364=0.096$バイト/サイクルになります。
データの読み出し命令は、命令全体の$250/1000=25%$であり、その内の2%がミスし、ミスするごとに1ブロック64バイトが呼び出されるので、1命令あたりに読み出されるバイト数は$250/10000.0264=0.32$バイト/命令になります。
よって1サイクルあたりに読み出されるバイト数は$0.32*0.5=0.16$バイト/サイクルになります。
ライトスルー方式なので、キャッシュミスしなくても、主記憶に対して毎回、1語=8バイトの書き込みが必要になります。
データの書き込み命令は、命令全体の$100/1000=10%$なので、1命令あたりに書き込まれるバイト数は$100/10008=0.8$バイト/命令なので、1サイクルあたりに書き込まれるミスするバイト数は$0.80.5=0.4$バイト/サイクルになります。
書き込みミス時には、主記憶からの読み出しが必要になります。
データの書き込み命令は、命令全体の$100/1000=10%$であり、その内の2%がミスし、ミスするごとに1ブロック64バイトが呼び出されるので、1命令あたりに読み出されるバイト数は$100/10000.0264=0.128$バイト/命令になります。
よって1サイクルあたりに読み出されるバイト数は$0.32*0.5=0.064$バイト/サイクルになります。
よって読み込みバンド幅は$0.096+0.16+0.064=0.32$バイト/サイクル、書き込みのバンド幅は0.4バイト/サイクルになります。
5.7.2
(未解答)
$0.5*(0.25+0.1)0.0264$
ライトバック方式なので、キャッシュミス時にしか主記憶へのデータ書き込みはしません。
ただし、書き込みミス時だけではなく、読み込みミス時にもデータの書き込みが必要になります。
(キャッシュラインが満杯になった場合を、ここでは考えません)
5.8
5.8.1
1ブロックあたり4語なので、$アドレス/4=n$を満たすアドレスを読み出し済みの場合、(それらのブロックが更新により置き換えられていなければ) $4n, 4n+1, 4n+1, 4n+2, 4*n+3$ を読んだ場合はキャッシュヒットします。
よって今回の問題の場合は $0, 4, 8, \cdots, 4n$ でキャッシュミスし、それ以外ではキャッシュ・ヒットします。
よってミス率は25%です。
また、これらのキャッシュミスの全ては、初めて読み込まれるブロックに対して発生しているので、初期参照ミスになります。
5.8.2
1ブロックあたり2語、8語、16語になるので、ミス率は50%、12.5%、6.25%です。
5.8.3
ミス率は0%です。
プリフェッチ・バッファは常に次の要求を満たします。
5.9
5.9.1
ブロックサイズが大きい程、データ転送要求されてから実際にデータ転送されるまでの時間は長くなります。
キャッシュミスした時のレイテンシをミス・レイテンシと呼びます。
ブロックサイズが8の時は、ミスした時のレイテンシが20×8で、ミス率は4%なので、平均で 0.04208=6.4 サイクルをデータ転送に要します。
ブロックサイズが16の時は、ミスした時のレイテンシが20×16で、ミス率は3%なので、平均で 0.032016=9.6 サイクルをデータ転送に要します。
ブロックサイズが32の時は、ミスした時のレイテンシが20×32で、ミス率は2%なので、平均で 0.022032=12.8 サイクルをデータ転送に要します。
ブロックサイズが64の時は、ミスした時のレイテンシが20×64で、ミス率は1.5%なので、平均で 0.0152064=19.2 サイクルをデータ転送に要します。
ブロックサイズが128の時は、ミスした時のレイテンシが20×128で、ミス率は1%なので、平均で 0.0120128=25.6 サイクルをデータ転送に要します。
よって最小なのはブロックサイズが8の時になります
5.9.2
ブロックサイズが8の時は、ミスした時のレイテンシが24+8で、ミス率は4%なので、平均で 0.04*(24+8)=1.28 サイクルをデータ転送に要します。
ブロックサイズが16の時は、ミスした時のレイテンシが24+16で、ミス率は3%なので、平均で 0.03*(24+16)=1.20 サイクルをデータ転送に要します。
ブロックサイズが32の時は、ミスした時のレイテンシが24+32で、ミス率は2%なので、平均で 0.02*(24+32)=1.12 サイクルをデータ転送に要します。
ブロックサイズが64の時は、ミスした時のレイテンシが24+64で、ミス率は1.5%なので、平均で 0.015*(24+64)=1.32 サイクルをデータ転送に要します。
ブロックサイズが128の時は、ミスした時のレイテンシが24+128で、ミス率は1%なので、平均で 0.01*(24+128)=1.52 サイクルをデータ転送に要します。
よって最小なのはブロックサイズが32の時になります
5.9.3
ミスした時のレイテンシが一定ならば、ミス率の最も低い場合に平均データ転送時間が最小になるので、ブロックサイズが128の時になります
5.10
5.10.1
P1のヒット時間は0.66nsなので、周波数は$10^9/0.66=1.515$GHz
P2のヒット時間は0.90nsなので、周波数は$10^9/0.90=1.111$GHz
5.10.2
AMATはヒットした場合のアクセス時間とミス率×ミスした場合のアクセス時間の和です。
よってP1のAMATは、毎回必ずキャッシュにアクセスし、8%の確率で主記憶にアクセスするので、0.66ns+0.0870ns=6.26nsです。
よってP2のAMATは、毎回必ずキャッシュにアクセスし、6%の確率で主記憶にアクセスするので、0.9ns+0.0670ns=5.1nsです。
5.10.3
ストールしない場合は、P1へのアクセス時間である0.66nsだけでメモリにアクセスできるので、基本CPIの1サイクルは0.66nsになります。
よって主記憶へのアクセスには70/0.66=106.06なので107サイクル要します。(サイクルに小数点はないので切り上げ)
P1のCPIの総数は、命令全体についてストールせずにアクセスできた1サイクル、命令全体について8%の確率でキャッシュミスして主記憶へのアクセスに要する107サイクル、36%の確率で発生する追加のメモリアクセスが必要な命令において8%の確率でキャッシュ・ミスして主記憶へのアクセスに要する107サイクルの和です。
つまり1+0.08107+0.360.08*107=12.641CPIになります。
ストールしない場合は、P2へのアクセス時間である0.90nsだけでメモリにアクセスできるので、基本CPIの1サイクルは0.90nsになります。
よって主記憶へのアクセスには70/0.90=77.78なので78サイクル要します。
P2のCPIの総数は、命令全体についてストールせずにアクセスできた1サイクル、命令全体について6%の確率でキャッシュミスして主記憶へのアクセスに要する78サイクル、36%の確率で発生する追加のメモリアクセスが必要な命令において6%の確率でキャッシュ・ミスして主記憶へのアクセスに要する78サイクルの和です。
つまり1+0.0678+0.360.08*78=7.365CPIになります。
5.10.4
P1のAMATは、毎回必ずキャッシュにアクセスし、8%の確率でL2にアクセスし、更に95%の確率で主記憶にアクセスするので、0.66ns+0.085.62ns+0.080.95*70ns=6.4296nsです。
よって今回の場合は、L2を追加したことで性能が悪化しています。
5.10.5
ストールしない場合は、P1へのアクセス時間である0.66nsだけでメモリにアクセスできるので、基本CPIの1サイクルは0.66nsになります。
よって主記憶へのアクセスには70/0.66=106.06なので107サイクル要します。(サイクルに小数点はないので切り上げ)
P1のCPIの総数は、命令全体についてストールせずにアクセスできた1サイクル、命令全体について8%の確率でキャッシュミスしてL2へのアクセスに要する5.62/0.66=8.515なので9サイクル、それが更に95%の確率でキャッシュミスして主記憶へのアクセスに要する107サイクル、36%の確率で発生する追加のメモリアクセスが必要な命令において8%の確率でキャッシュミスしてL2へのアクセスに要する9サイクル、それが更に95%の確率でキャッシュミスして主記憶へのアクセスに要する107サイクルの和です。
つまり1+(1+0.36)(0.089+0.080.95107)=13.572CPIになります。
5.10.6
$0.66ns+0.085.62ns+0.08x*70ns<6.26$となるように、キャッシュミスの確率$x$を選びます。
計算によりxが91.97%以下の場合に、この式が成立します。
5.10.7
$0.66ns+0.085.62ns+0.08x*70ns<5.1$ となるように、キャッシュミスの確率 $x$を選びます。
計算によりxが71.26%以下の場合に、この式が成立します。
5.11
5.11.1
3wayなので2ブロックが3個並び、1ライン6ブロックで48/6=8ラインになります。
ブロック・サイズが2語なので、最下位1ビットはオフセットです。
ライン数は8=$2^3$なので、インデックスは最下位を除く下位3ビットです。
タグは残りの上位4ビットになります。
5.11.2
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | 3way |
|---|---|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x0 | 1 | 1 | ミス | Way0(1)=0追加 |
| 0xb4 | 1011 0100 | 0xb | 2 | 0 | ミス | Way0(2)=b追加 |
| 0x2b | 0010 1011 | 0x2 | 5 | 1 | ミス | Way0(5)=2追加 |
| 0x02 | 0000 0010 | 0x0 | 1 | 0 | ヒット | |
| 0xbe | 1011 1110 | 0xb | 7 | 0 | ミス | Way0(7)=b追加 |
| 0x58 | 0101 1000 | 0x5 | 4 | 0 | ミス | Way0(4)=5追加 |
| 0xbf | 1011 1111 | 0xb | 7 | 1 | ヒット | |
| 0x0e | 0000 1110 | 0x0 | 7 | 0 | ミス | Way1(7)=0追加 |
| 0x1f | 0001 1111 | 0x1 | 7 | 1 | ミス | Way2(7)=1追加 |
| 0xb5 | 1011 0101 | 0xb | 2 | 1 | ヒット | |
| 0xbf | 1011 1111 | 0xb | 7 | 1 | ヒット | |
| 0xba | 1011 1010 | 0xb | 5 | 0 | ミス | Way1(5)=b追加 |
| 0x2e | 0010 1110 | 0x2 | 7 | 0 | ミス | Way1(7)=2更新 |
| 0xce | 1100 1110 | 0xc | 7 | 0 | ミス | Way2(7)=0更新 |
置換方式はLRU。よって0xbfではway0にヒットしているので、0x2eでインデックス7番の更新が必要な時に最古の参照キャッシュはway1なので、way1を更新します。
次に0xceでインデックス7番の更新が必要な時は、最古の参照キャッシュはway2なので、way2を更新します。
5.11.3
フル・アソシアティブ方式は1ラインです。
ブロック・サイズが1語なので、オフセットはありません。
ライン数は1なので、インデックスもありません。
タグはデータそのものである8ビットになります。
5.11.4
異なるアドレスは必ずミスし、同じアドレスは必ずヒットします。
置換はLRU方式なので、キャッシュが8語で満杯の時にミスすれば1番目のアドレスが削除され、8番目に新しいアドレスが追加されます。
ヒットすれば、ヒットしたアドレスが8番目に来ます。
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | キャッシュ |
|---|---|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x03 | なし | なし | ミス | 0x03追加 |
| 0xb4 | 1011 0100 | 0xb4 | なし | なし | ミス | 0xb4追加 |
| 0x2b | 0010 1011 | 0x2b | なし | なし | ミス | 0x2b追加 |
| 0x02 | 0000 0010 | 0x02 | なし | なし | ミス | 0x02追加 |
| 0xbe | 1011 1110 | 0xbe | なし | なし | ミス | 0xbe追加 |
| 0x58 | 0101 1000 | 0x58 | なし | なし | ミス | 0x58追加 |
| 0xbf | 1011 1111 | 0xbf | なし | なし | ミス | 0xbf追加 |
| 0x0e | 0000 1110 | 0x0e | なし | なし | ミス | 0x0e追加 |
| 0x1f | 0001 1111 | 0x1f | なし | なし | ミス | 0x1f追加,0x03削除 |
| 0xb5 | 1011 0101 | 0xb5 | なし | なし | ミス | 0xb5追加,0xb4削除 |
| 0xbf | 1011 1111 | 0xbf | なし | なし | ヒット | |
| 0xba | 1011 1010 | 0xba | なし | なし | ミス | 0xba追加,0x2b削除 |
| 0x2e | 0010 1110 | 0x2e | なし | なし | ミス | 0x2e追加,0x02削除 |
| 0xce | 1100 1110 | 0xce | なし | なし | ミス | 0xce追加,0xbe削除 |
5.11.5
フル・アソシアティブ方式は1ラインです。
ブロック・サイズが2語なので、最下位1ビットはオフセットです。
ライン数は1なので、インデックスはありません。
タグはデータ8-1=7ビットになります。
5.11.6
置換はLRU方式なので、キャッシュが8語で満杯の時にミスすれば1番目のアドレス2語が削除され、4番目に新しいアドレス2語が追加されます。
ヒットすれば、ヒットしたアドレス2語が4番目に来ます。
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | キャッシュ |
|---|---|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x01 | なし | 1 | ミス | [0x02,0x03] |
| 0xb4 | 1011 0100 | 0x5a | なし | 0 | ミス | [0x02,0x03],[0xb4,0xb5] |
| 0x2b | 0010 1011 | 0x15 | なし | 1 | ミス | [0x02,0x03],[0xb4,0xb5],[0x2a,0x2b] |
| 0x02 | 0000 0010 | 0x01 | なし | 0 | ヒット | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03] |
| 0xbe | 1011 1110 | 0x5f | なし | 0 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0xbe,0xbf] |
| 0x58 | 0101 1000 | 0x2c | なし | 0 | ミス | [0x2a,0x2b],[0x02,0x03],[0xbe,0xbf],[0x58,0x59] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ヒット | [0x2a,0x2b],[0x02,0x03],[0x58,0x59],[0xbe,0xbf] |
| 0x0e | 0000 1110 | 0x07 | なし | 0 | ミス | [0x02,0x03],[0x58,0x59],[0xbe,0xbf],[0x0e,0x0f] |
| 0x1f | 0001 1111 | 0x0f | なし | 1 | ミス | [0x58,0x59],[0xbe,0xbf],[0x0e,0x0f],[0x1e,0x1f] |
| 0xb5 | 1011 0101 | 0x5a | なし | 1 | ミス | [0xbe,0xbf],[0x0e,0x0f],[0x1e,0x1f],[0xb4,0xb5] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ヒット | [0x0e,0x0f],[0x1e,0x1f],[0xb4,0xb5],[0xbe,0xbf] |
| 0xba | 1011 1010 | 0x5d | なし | 0 | ミス | [0x1e,0x1f],[0xb5,0xb6],[0xbe,0xbf],[0xba,0xbb] |
| 0x2e | 0010 1110 | 0x17 | なし | 0 | ミス | [0xb4,0xb5],[0xbe,0xbf],[0xba,0xbb],[0x2e,0x2f] |
| 0xce | 1100 1110 | 0x67 | なし | 0 | ミス | [0xbe,0xbf],[0xba,0xbb],[0x2e,0x2f],[0xce,0xcf] |
5.11.7
置換はMRU方式なので、キャッシュが8語で満杯の時にミスすれば4番目のアドレス2語が削除され、4番目に新しいアドレス2語が追加されます。
ヒットすれば、ヒットしたアドレス2語が4番目に来ます。
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | キャッシュ |
|---|---|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x01 | なし | 1 | ミス | [0x02,0x03] |
| 0xb4 | 1011 0100 | 0x5a | なし | 0 | ミス | [0x02,0x03],[0xb4,0xb5] |
| 0x2b | 0010 1011 | 0x15 | なし | 1 | ミス | [0x02,0x03],[0xb4,0xb5],[0x2a,0x2b] |
| 0x02 | 0000 0010 | 0x01 | なし | 0 | ヒット | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03] |
| 0xbe | 1011 1110 | 0x5f | なし | 0 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0xbe,0xbf] |
| 0x58 | 0101 1000 | 0x2c | なし | 0 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0x58,0x59] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0xbe,0xbf] |
| 0x0e | 0000 1110 | 0x07 | なし | 0 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0x0e,0x0f] |
| 0x1f | 0001 1111 | 0x0f | なし | 1 | ミス | [0xb4,0xb5],[0x2a,0x2b],[0x02,0x03],[0x1e,0x1f] |
| 0xb5 | 1011 0101 | 0x5a | なし | 1 | ヒット | [0x2a,0x2b],[0x02,0x03],[0x1e,0x1f],[0xb4,0xb5] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ミス | [0x2a,0x2b],[0x02,0x03],[0x1e,0x1f],[0xbe,0xbf] |
| 0xba | 1011 1010 | 0x5d | なし | 0 | ミス | [0x2a,0x2b],[0x02,0x03],[0x1e,0x1f],[0xba,0xbb] |
| 0x2e | 0010 1110 | 0x17 | なし | 0 | ミス | [0x2a,0x2b],[0x02,0x03],[0x1e,0x1f],[0x2e,0x2f] |
| 0xce | 1100 1110 | 0x67 | なし | 0 | ミス | [0x2a,0x2b],[0x02,0x03],[0x1e,0x1f],[0xce,0xcf] |
5.11.8
置換は最適化方式ですが、この方式に実用的な意味があるのかよく分かりませんでした。
何が最適であるかは、未来にどのアドレスを参照するかを知らないと分かりません。
本問ではあらかじめ全てのアドレスが分かっているので最適な置換ができますが、現実にも同様のケースがあるのか知りたいところです。
未来に重複するタグ、0x01、0x5f、0x5aがヒットできるように、これらをキャッシュから削除しないようにします。
| 16進アドレス | 2進アドレス | タグ | インデックス | オフセット | ヒット | キャッシュ |
|---|---|---|---|---|---|---|
| 0x03 | 0000 0011 | 0x01 | なし | 1 | ミス | [0x02,0x03] |
| 0xb4 | 1011 0100 | 0x5a | なし | 0 | ミス | [0x02,0x03],[0xb4,0xb5] |
| 0x2b | 0010 1011 | 0x15 | なし | 1 | ミス | [0x02,0x03],[0xb4,0xb5],[0x2a,0x2b] |
| 0x02 | 0000 0010 | 0x01 | なし | 0 | ヒット | [0x02,0x03],[0xb4,0xb5],[0x2a,0x2b] |
| 0xbe | 1011 1110 | 0x5f | なし | 0 | ミス | [0x02,0x03],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0x58 | 0101 1000 | 0x2c | なし | 0 | ミス | [0x58,0x59],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ヒット | [0x58,0x59],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0x0e | 0000 1110 | 0x07 | なし | 0 | ミス | [0x0e,0x0f],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0x1f | 0001 1111 | 0x0f | なし | 1 | ミス | [0x1e,0x1f],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0xb5 | 1011 0101 | 0x5a | なし | 1 | ヒット | [0x1e,0x1f],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0xbf | 1011 1111 | 0x5f | なし | 1 | ヒット | [0x1e,0x1f],[0xb4,0xb5],[0x2a,0x2b],[0xbe,0xbf] |
| 0xba | 1011 1010 | 0x5d | なし | 0 | ミス | [0x1e,0x1f],[0xb4,0xb5],[0xba,0xbb],[0xbe,0xbf] |
| 0x2e | 0010 1110 | 0x17 | なし | 0 | ミス | [0x1e,0x1f],[0xb4,0xb5],[0x2e,0x2f],[0xbe,0xbf] |
| 0xce | 1100 1110 | 0x67 | なし | 0 | ミス | [0x1e,0x1f],[0xb4,0xb5],[0xce,0xcf],[0xbe,0xbf] |
5.12
5.12.1
第1レベル・キャッシュだけを使用した場合
主記憶へのアクセスに要するCPIは100ns/2GHz = $10010^9/(1/210^9)=200$サイクルです。
7%がキャッシュミスして主記憶にアクセスするので、平均で$0.07*200 = 14$サイクルを要します。
よって$1.5 + 14 = 15.5$サイクルかかることになります。
主記憶へのアクセス時間が倍になった場合は、主記憶へのアクセスに要するCPIは200ns/2GHz = $20010^9/(1/210^9)=400$サイクルです。
7%がキャッシュミスして主記憶にアクセスするので、平均で$0.07*400 = 28$サイクルを要します。
よって$1.5 + 28 = 29.5$サイクルかかることになります。
ダイレクトマップ方式の第2レベル・キャッシュも使用した場合
7%がキャッシュミスして2次キャッシュにアクセスするので、平均で$0.0712 = 0.84$サイクルを要します。
7%の内の3.5%は2次キャッシュにもミスして主記憶にアクセスするので、平均で$0.070.035*200 = 0.49$サイクルを要します。
よって$1.5 + 0.84 + 0.49 = 2.83$サイクルかかることになります。
主記憶へのアクセス時間が倍になった場合は、7%の内の3.5%は2次キャッシュにもミスして主記憶にアクセスするので、平均で$0.070.035400 = 0.98$サイクルを要します。
よって$1.5 + 0.84 + 0.98 = 3.32$サイクルかかることになります。
8ウェイ・セット・アソシアティブ方式の第2レベル・キャッシュも使用した場合
7%がキャッシュミスして2次キャッシュにアクセスするので、平均で$0.0728 = 1.96$サイクルを要します。
7%の内の1.5%は2次キャッシュにもミスして主記憶にアクセスするので、平均で$0.070.015*200 = 0.21$サイクルを要します。
よって$1.5 + 1.96 + 0.21 = 3.67$サイクルかかることになります。
主記憶へのアクセス時間が倍になった場合は、7%の内の1.5%は2次キャッシュにもミスして主記憶にアクセスするので、平均で$0.070.015400 = 0.42$サイクルを要します。
よって$1.5 + 1.96 + 0.42 = 3.88$サイクルかかることになります。
以上より主記憶にアクセスする時間が長くなると、サイクル時間の増加率は2次キャッシュを使う方が低くなり、8ウェイ・セット・アソシアティブ方式の方がダイレクトマップ方式よりも増加率が低くなります。
15.12.2
7%がキャッシュミスして2次キャッシュにアクセスするので、平均で$0.0712 = 0.84$サイクルを要します。
7%の内の3.5%は2次キャッシュにもミスして3次キャッシュにアクセスするので、平均で$0.070.03550= 0.125$サイクルを要します。
7%の内の3.5%の更に13%は3次キャッシュにもミスして主記憶にアクセスするので、平均で$0.070.0350.13200 = 0.0637$サイクルを要します。
よって$1.5 + 0.84 + 0.125 + 0.0637 = 2.5287$サイクルかかることになります。
3次キャッシュの利点はCPIを減らせることです。
欠点は、製造コストや消費電力の増加、制御の複雑化などだと思います。
15.12.3
キャッシュ全体のアクセスが50サイクル、という問題文の意味が分かりませんでした。
1次キャッシュと2次キャッシュへのアクセスに50サイクルかかると解釈しました。
7%がキャッシュミスして2次キャッシュにアクセスするので、平均で$0.0750 = 3.5$サイクルを要します。
7%の内の4%は2次キャッシュにもミスして主記憶にアクセスするので、平均で$0.07(0.04-0.007n)*200 = 0.56-0.098n$サイクルを要します。
この0.56-0.098nがダイレクトマップ方式の2次キャッシュの0.49サイクルよりも小さくなるためには0.07サイクル以上短くすればいいので、n=1であればよく、キャッシュを512KiBだけ大きくする必要があります。
15.13
15.13.1
MTBFはMTTFとMTTRの和なので3年と1日になります。
15.13.2
可用性はMTTF/(MTTF+MTTR)なので3年/3年+1日で99.9%です。
15.13.3
MTTRが0に近づくほど可用性は1に近づきます。
現実にはそのような性能は出せないと思われます。
15.13.4
MTTRが大きくなるほど可用性は小さくなります。
ですが、MTTFが十分にMTTRより大きければ、MTTRの増加の影響は軽微になり、デバイスの可用性を少ししか下げません。
つまりMTTRが大きくても、必ずデバイスの可用性が低いとは限りません。
15.14
15.14.1
SECに必要なビット数は、パリティビット数を$p$個、データビット数を$d$個として$2^p \geq p+d+1$を満たします。
128ビットのデータは$2^p \geq p+128+1$を満たす最小のpは8です。
SED、つまり2ビット誤り訂正するにはパリティビットを1ビット追加するので、必要なパリティビットは9になります。
15.14.2
64ビットデータに対して8ビットのパリティビットが必要な場合は、パリティビットが全データの8/72=11%を占めます。
128ビットデータに対して9ビットのパリティビットが必要な場合は、パリティビットが全データの9/137=6.5%を占めます。
もし128ビットのデータがある時、前者は2ビット分の誤り訂正ができ、後者は1ビット分の誤り訂正しかできません。
よって全データに対する誤り訂正効率比は、前者:後者で11/2=5.5:6.5/1=6.5です。
よって64ビットデータに対して8ビットのパリティビットをつける方が誤り訂正効率が良いことになります。
15.14.3
0x375 = 0b0011_0111_0101
| p1 | p2 | d1 | p4 | d2 | d3 | d4 | p8 | d5 | d6 | d7 | d8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| data | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| P1 | X | X | X | X | X | X | ||||||
| P2 | X | X | X | X | X | X | ||||||
| P4 | X | X | X | X | X | |||||||
| P8 | X | X | X | X | X |
P1のチェック対象のビットは0,1,0,1,0,0です。パリティを偶とするためにはP1=0となるべきなので正しいです。
P2のチェック対象のビットは0,1,1,1,1,0です。パリティを偶とするためにはP2=0となるべきなので正しいです。
P4のチェック対象のビットは1,0,1,1,1です。パリティを偶とするためにはP4=1となるべきなので正しいです。
P8のチェック対象のビットは1,0,1,0,1です。パリティを偶とするためにはP8=0となるべきなので誤りです。
つまりP8が誤りなので8番目のデータであるP8を反転させた0x365が正しいデータと分かります。
5.15
5.15.1
問題文で与えられているBツリーの深さは、要素数を$E$とすれば、$\log_2 E$になります。
要素数はエントリーの総数なので、全ページサイズの70%がエントリーされていることから、ページサイズ/1エントリーのサイズ×70%になります。
インデックスページへのアクセスコストは、レイテンシ10ms + 転送に要する時間です。
転送に要する時間は、ページサイズ/10Mバイト毎秒です。(2KiBのページサイズならば、転送時間は0.2msec)
エントリサイズが16バイトから128バイトになれば、ページユーティリティとユーティリティ・コストが以下のように変化するので、最善のページサイズは32KiBです。
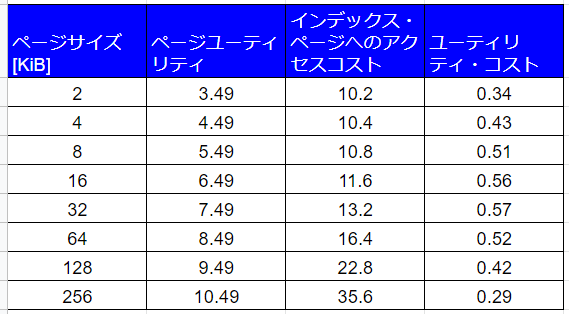
5.15.2
全ページサイズの50%がエントリーされているとすれば、ページユーティリティとユーティリティ・コストが以下のように変化するので、最善のページサイズは32KiBです。
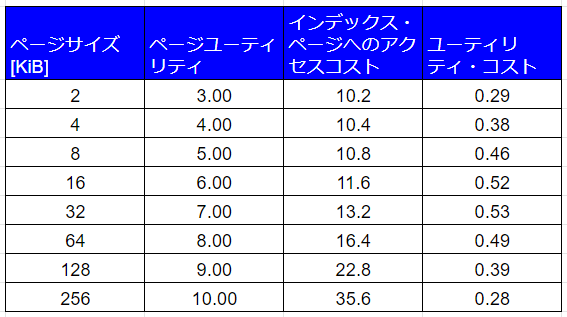
5.15.3
レイテンシが短くなり、転送速度が向上すると、インデックス・ページへのアクセスコストとユーティリティ・コストが以下のように変化するので、最善のページサイズは64KiBです。

性能が向上するほど、ページ・サイズが大きい方が性能が良くなることが分かります。
5.15.4
ページサイズを同じに維持するならば、DRAMのコストを下げるか、ディスク・アクセス率を上げるしかありません。
DRAMの値段はここ10年で劇的に下がってはいないので、ディスク・アクセス率を上げる方が現実的と思われます。
5.16
本問の私の解答は間違っている気がします。
5.16.1
ページサイズは4KiB=4096バイト=$2^{12}$バイトなので、仮想記憶のページとタグはアドレスの上位4ビットになります。
フルアソシアティブ方式なのでインデックスはありません。ページテーブルへのアクセスにミスすることもありません。
アドレス0x123dのタグは0x1なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では、ページ0x1はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号12の次のページの13を使用します。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0xb | 12 | 5 |
| 1 | 0x7 | 4 | 2 |
| 1 | 0x3 | 6 | 4 |
| 1 | 0x1 | 13 | 0 |
アドレス0x08b3のタグは0x0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では物理ページ5にあります。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x0 | 5 | 0 |
| 1 | 0x7 | 4 | 3 |
| 1 | 0x3 | 6 | 5 |
| 1 | 0x1 | 13 | 1 |
アドレス0x365cのタグは0x3なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x0 | 5 | 1 |
| 1 | 0x7 | 4 | 4 |
| 1 | 0x3 | 6 | 0 |
| 1 | 0x1 | 13 | 2 |
アドレス0x871bのタグは0x8なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ2を置き換えます。
ページテーブル上では、ページ0x8はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号13の次のページの14を使用します。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x0 | 5 | 2 |
| 1 | 0x8 | 14 | 0 |
| 1 | 0x3 | 6 | 1 |
| 1 | 0x1 | 13 | 3 |
アドレス0xbee6のタグは0xbなのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では物理ページ12にあります。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x0 | 5 | 3 |
| 1 | 0x8 | 14 | 1 |
| 1 | 0x3 | 6 | 2 |
| 1 | 0xb | 12 | 0 |
アドレス0x3140のタグは0x3なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x0 | 5 | 4 |
| 1 | 0x8 | 14 | 2 |
| 1 | 0x3 | 6 | 0 |
| 1 | 0xb | 12 | 1 |
アドレス0xc049のタグは0xcなのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では、ページ0xcはディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号14の次のページの15を使用します。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0xc | 15 | 0 |
| 1 | 0x8 | 14 | 3 |
| 1 | 0x3 | 6 | 1 |
| 1 | 0xb | 12 | 2 |
15.16.2
ページサイズは16KiB=$2^{14}$バイトなので、仮想記憶のページとタグはアドレスの上位2ビットになります。
フルアソシアティブ方式なのでインデックスはありません。ページテーブルへのアクセスにミスすることもありません。
アドレス0x123dのタグは0x0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では物理ページ5にあります。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0xb | 12 | 5 |
| 1 | 0x7 | 4 | 2 |
| 1 | 0x3 | 6 | 4 |
| 1 | 0x0 | 5 | 0 |
アドレス0x08b3のタグは0x0なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0xb | 12 | 6 |
| 1 | 0x7 | 4 | 3 |
| 1 | 0x3 | 6 | 5 |
| 1 | 0x0 | 5 | 0 |
アドレス0x3b5cのタグは0x0なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0xb | 12 | 7 |
| 1 | 0x7 | 4 | 4 |
| 1 | 0x3 | 6 | 6 |
| 1 | 0x0 | 5 | 0 |
アドレス0x871bのタグは0x2なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では、ページ0x2はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号12の次のページの13を使用します。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x2 | 13 | 0 |
| 1 | 0x7 | 4 | 5 |
| 1 | 0x3 | 6 | 7 |
| 1 | 0x0 | 5 | 1 |
アドレス0xbee6のタグは0x0なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x2 | 13 | 0 |
| 1 | 0x7 | 4 | 6 |
| 1 | 0x3 | 6 | 8 |
| 1 | 0x0 | 5 | 2 |
アドレス0x3140のタグは0x0なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x2 | 13 | 1 |
| 1 | 0x7 | 4 | 7 |
| 1 | 0x3 | 6 | 9 |
| 1 | 0x0 | 5 | 2 |
アドレス0xc040のタグは0x3なのでTLBはヒットします。
| 有効 | タグ | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|
| 1 | 0x2 | 13 | 2 |
| 1 | 0x7 | 4 | 8 |
| 1 | 0x3 | 6 | 0 |
| 1 | 0x0 | 5 | 3 |
15.16.3
ページサイズは4KiB=4096バイト=$2^{12}$バイトです。
仮想記憶のページは上位4ビットですが、2ウェイ・セット・アソシアティブ方式なので4番目のビットはインデックスになり、残りの上位3ビットがタグになります。
アドレス0x123dのタグは0b000であり、インデックスは1なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では、ページ1はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号12の次のページの13を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b101 | 0 | 12 | 5 |
| 1 | 0b011 | 1 | 4 | 2 |
| 1 | 0b001 | 1 | 6 | 4 |
| 1 | 0b000 | 1 | 13 | 0 |
アドレス0x08b3のタグは0b000であり、インデックスは0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では物理ページ5にあります。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b000 | 0 | 5 | 0 |
| 1 | 0b011 | 1 | 4 | 3 |
| 1 | 0b001 | 1 | 6 | 5 |
| 1 | 0b000 | 1 | 13 | 1 |
アドレス0x365cのタグは0b001であり、インデックスは1なのでTLBはヒットします。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b000 | 0 | 5 | 1 |
| 1 | 0b011 | 1 | 4 | 4 |
| 1 | 0b001 | 1 | 6 | 0 |
| 1 | 0b000 | 1 | 13 | 2 |
アドレス0x871bのタグは0b100であり、インデックスは0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ2を置き換えます。
ページテーブル上では、ページ8はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号13の次のページの14を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b000 | 0 | 5 | 2 |
| 1 | 0b100 | 0 | 14 | 0 |
| 1 | 0b001 | 1 | 6 | 1 |
| 1 | 0b000 | 1 | 13 | 3 |
アドレス0xbee6のタグは0b101であり、インデックスは0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では物理ページ12にあります。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b000 | 0 | 5 | 3 |
| 1 | 0b100 | 0 | 14 | 1 |
| 1 | 0b001 | 1 | 6 | 2 |
| 1 | 0b101 | 0 | 12 | 0 |
アドレス0xc049のタグは0b110であり、インデックスは0なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では、ページ6はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号14の次のページの15を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b110 | 0 | 15 | 0 |
| 1 | 0b100 | 0 | 14 | 2 |
| 1 | 0b001 | 1 | 6 | 3 |
| 1 | 0b101 | 0 | 12 | 1 |
15.16.4
ページサイズは4KiB=4096バイト=$2^{12}$バイトです。
仮想記憶のページは上位4ビットですが、ダイレクトマップ方式なので、エントリの数$4=2^2$より4ビットの内の下位2ビットがインデックスで、残りの上位2ビットがタグになります。
アドレス0x123dのタグは0b00であり、インデックスはb01なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では、ページ1はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号12の次のページの13を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b10 | b10 | 12 | 5 |
| 1 | 0b01 | b11 | 4 | 2 |
| 1 | 0b00 | b11 | 6 | 4 |
| 1 | 0b00 | b01 | 13 | 0 |
アドレス0x08b3のタグは0b00であり、インデックスはb00なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ1を置き換えます。
ページテーブル上では物理ページ5にあります。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b00 | b00 | 5 | 0 |
| 1 | 0b01 | b11 | 4 | 3 |
| 1 | 0b00 | b11 | 6 | 5 |
| 1 | 0b00 | b01 | 13 | 1 |
アドレス0x365cのタグは0b00であり、インデックスはb11なのでTLBはヒットします。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b00 | b00 | 5 | 1 |
| 1 | 0b01 | b11 | 4 | 4 |
| 1 | 0b00 | b11 | 6 | 0 |
| 1 | 0b00 | b01 | 13 | 2 |
アドレス0x871bのタグは0b10であり、インデックスはb00なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ2を置き換えます。
ページテーブル上では、ページ8はディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号13の次のページの14を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b00 | b00 | 5 | 2 |
| 1 | 0b10 | b00 | 14 | 0 |
| 1 | 0b00 | b11 | 6 | 1 |
| 1 | 0b00 | b01 | 13 | 3 |
アドレス0x3140のタグは0b00であり、インデックスはb11なのでTLBはヒットします。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b00 | b00 | 5 | 3 |
| 1 | 0b10 | b00 | 14 | 1 |
| 1 | 0b00 | b11 | 6 | 0 |
| 1 | 0b00 | b01 | 13 | 4 |
アドレス0xc049のタグは0b11であり、インデックスはb00なのでTLBはミスします。
TLBの前回アクセス時間が最も大きなタグ4を置き換えます。
ページテーブル上では、ページcはディスクにあるのでページフォルトします。
よってTLBの最大の物理ページ番号14の次のページの15を使用します。
| 有効 | タグ | インデックス | 物理ページ番号 | 前回アクセス後の時間 |
|---|---|---|---|---|
| 1 | 0b00 | b00 | 5 | 4 |
| 1 | 0b10 | b00 | 14 | 2 |
| 1 | 0b00 | b11 | 6 | 1 |
| 1 | 0b11 | b00 | 15 | 0 |
15.16.5
TLBがなければ毎回、主記憶にあるページテーブルを参照することになります。
TLBがあることで主記憶にアクセスする頻度を減らせます。
15.17
15.17.1
ページサイズが8KiB=8192バイト=$2^{13}$なのでインデックスは13ビットです。よってタグは32-12=19ビットになります。
5つのアプリケーションの各々で1ページ・テーブルあたり4バイトが$2^{19}$ページ・テーブルあるので、54524288=10,485,760バイトが総ページサイズになります。
15.17.2
第2レベルがそれぞれ第1レベル$256=2^8$を持つとすれば、第2レベルのエントリー総数は$2^{19-8}=2^{11}=2048$個になります。
第2レベルのサイズは、1エントリあたり6バイトなので20486=12,288バイトになります。
一方で仮想アドレス空間は20488KiB=16,384KiBをカバーします。
15.17.3
1ブロックは2*64/8=16バイトなので、16KiBのキャッシュは16KiB/16=1024=$2^{10}$ブロックを持ちます。よってインデックスは10ビットになります。
ブロックは16=$2^4$バイトなのでオフセットは4ビットになります。
合計で14ビットになるので、ページのインデックスである13ビットを超えてしまいます。
よってキャッシュのデータサイズを2倍にすればページのインデックスは同じ14ビットになります。
15.18
15.18.1
ページ・サイズは4KiB=4096バイト=$2^{12}$バイトなので、エントリ数は$2^{43-12}$=2,147,483,648です。
PTEサイズは4バイトなので、必要なメモリサイズは4*2,147,483,648=8,589,934,592バイトになります。
15.18.2
5.19
5.20
5.20.1
2ウェイ・セット・アソシアティブの場合、ブロック番号をセット数の2で剰余を取った数が、ブロックが含まれるセット位置になります。
置換はLRU方式なので、最も古く参照されたブロックを置き換えていきます。
| アドレス | ヒット | キャッシュのセット | セット0 | セット0 | セット1 | セット1 |
|---|---|---|---|---|---|---|
| 0 | ミス | 0 mod 2 = 0 | メモリ[0]new | |||
| 1 | ミス | 1 mod 2 = 1 | メモリ[0]new | メモリ[1]new | ||
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2]new | メモリ[1]new | |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4]new | メモリ[2] | メモリ[1] | メモリ[3]new |
| 2 | ヒット | 2 mod 2 = 0 | メモリ[4] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 3 | ヒット | 3 mod 2 = 1 | メモリ[4] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 4 | ヒット | 4 mod 2 = 0 | メモリ[4]new | メモリ[2] | メモリ[1] | メモリ[3]new |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4]new | メモリ[2] | メモリ[5]new | メモリ[3] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[4] | メモリ[6]new | メモリ[5]new | メモリ[3] |
| 7 | ミス | 7 mod 2 = 1 | メモリ[4] | メモリ[6]new | メモリ[5] | メモリ[7]new |
| 0 | ミス | 0 mod 2 = 0 | メモリ[0]new | メモリ[6] | メモリ[5] | メモリ[7]new |
| 1 | ミス | 1 mod 2 = 1 | メモリ[0]new | メモリ[6] | メモリ[1]new | メモリ[7] |
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2]new | メモリ[1]new | メモリ[7] |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4]new | メモリ[2] | メモリ[1] | メモリ[3]new |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4]new | メモリ[2] | メモリ[5]new | メモリ[3] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[4] | メモリ[6]new | メモリ[5]new | メモリ[3] |
| 7 | ミス | 7 mod 2 = 1 | メモリ[4] | メモリ[6]new | メモリ[5] | メモリ[7]new |
| 0 | ミス | 0 mod 2 = 0 | メモリ[0]new | メモリ[6] | メモリ[5] | メモリ[7]new |
5.20.2
置換はMRU方式なので、最も最近に参照されたブロックを置き換えていきます。
| アドレス | ヒット | キャッシュのセット | セット0 | セット0 | セット1 | セット1 |
|---|---|---|---|---|---|---|
| 0 | ミス | 0 mod 2 = 0 | メモリ[0]new | |||
| 1 | ミス | 1 mod 2 = 1 | メモリ[0]new | メモリ[1]new | ||
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2]new | メモリ[1]new | |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 4 | ミス | 4 mod 2 = 0 | メモリ[0] | メモリ[4]new | メモリ[1] | メモリ[3]new |
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 3 | ヒット | 3 mod 2 = 1 | メモリ[0] | メモリ[2]new | メモリ[1] | メモリ[3]new |
| 4 | ミス | 4 mod 2 = 0 | メモリ[0] | メモリ[4]new | メモリ[1] | メモリ[3]new |
| 5 | ミス | 5 mod 2 = 1 | メモリ[0] | メモリ[4]new | メモリ[1] | メモリ[5]new |
| 6 | ミス | 6 mod 2 = 0 | メモリ[0] | メモリ[6]new | メモリ[1] | メモリ[5]new |
| 7 | ミス | 7 mod 2 = 1 | メモリ[0] | メモリ[6]new | メモリ[1] | メモリ[7]new |
| 0 | ヒット | 0 mod 2 = 0 | メモリ[0]new | メモリ[6] | メモリ[1] | メモリ[7]new |
| 1 | ヒット | 1 mod 2 = 1 | メモリ[0]new | メモリ[6] | メモリ[1]new | メモリ[7] |
| 2 | ミス | 2 mod 2 = 0 | メモリ[2]new | メモリ[6] | メモリ[1]new | メモリ[7] |
| 3 | ミス | 3 mod 2 = 1 | メモリ[2]new | メモリ[6] | メモリ[3]new | メモリ[7] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4]new | メモリ[6] | メモリ[3]new | メモリ[7] |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4]new | メモリ[6] | メモリ[5]new | メモリ[7] |
| 6 | ヒット | 6 mod 2 = 0 | メモリ[4] | メモリ[6]new | メモリ[5]new | メモリ[7] |
| 7 | ヒット | 7 mod 2 = 1 | メモリ[4] | メモリ[6]new | メモリ[5] | メモリ[7]new |
| 0 | ミス | 0 mod 2 = 0 | メモリ[4] | メモリ[0]new | メモリ[5] | メモリ[7]new |
5.20.3
置換はランダム方式なので、その場の気分で置き換えていきます。
ものすごく運が悪いせいでミス率が可能な組み合わせの中で最大になる気がします。
| アドレス | ヒット | キャッシュのセット | セット0 | セット0 | セット1 | セット1 |
|---|---|---|---|---|---|---|
| 0 | ミス | 0 mod 2 = 0 | メモリ[0] | |||
| 1 | ミス | 1 mod 2 = 1 | メモリ[0] | メモリ[1] | ||
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[1] | |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[3] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[0] | メモリ[4] | メモリ[1] | メモリ[3] |
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[3] |
| 3 | ヒット | 3 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[3] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[3] |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4] | メモリ[2] | メモリ[5] | メモリ[3] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[4] | メモリ[6] | メモリ[5] | メモリ[3] |
| 7 | ミス | 7 mod 2 = 1 | メモリ[4] | メモリ[6] | メモリ[7] | メモリ[3] |
| 0 | ミス | 0 mod 2 = 0 | メモリ[0] | メモリ[6] | メモリ[7] | メモリ[3] |
| 1 | ミス | 1 mod 2 = 1 | メモリ[0] | メモリ[6] | メモリ[7] | メモリ[1] |
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[7] | メモリ[1] |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[3] | メモリ[1] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4] | メモリ[2] | メモリ[3] | メモリ[1] |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4] | メモリ[2] | メモリ[5] | メモリ[1] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[4] | メモリ[6] | メモリ[5] | メモリ[1] |
| 7 | ミス | 7 mod 2 = 1 | メモリ[4] | メモリ[6] | メモリ[5] | メモリ[7] |
| 0 | ミス | 0 mod 2 = 0 | メモリ[0] | メモリ[6] | メモリ[5] | メモリ[7] |
5.20.4
最適な置換をします。
| アドレス | ヒット | キャッシュのセット | セット0 | セット0 | セット1 | セット1 |
|---|---|---|---|---|---|---|
| 0 | ミス | 0 mod 2 = 0 | メモリ[0] | |||
| 1 | ミス | 1 mod 2 = 1 | メモリ[0] | メモリ[1] | ||
| 2 | ミス | 2 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[1] | |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[3] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[3] |
| 2 | ヒット | 2 mod 2 = 0 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[3] |
| 3 | ヒット | 3 mod 2 = 1 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[3] |
| 4 | ヒット | 4 mod 2 = 0 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[3] |
| 5 | ミス | 5 mod 2 = 1 | メモリ[4] | メモリ[2] | メモリ[1] | メモリ[5] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[6] | メモリ[2] | メモリ[1] | メモリ[5] |
| 7 | ミス | 7 mod 2 = 1 | メモリ[6] | メモリ[2] | メモリ[1] | メモリ[7] |
| 0 | ミス | 0 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[7] |
| 1 | ヒット | 1 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[7] |
| 2 | ヒット | 2 mod 2 = 0 | メモリ[0] | メモリ[2] | メモリ[1] | メモリ[7] |
| 3 | ミス | 3 mod 2 = 1 | メモリ[0] | メモリ[2] | メモリ[3] | メモリ[7] |
| 4 | ミス | 4 mod 2 = 0 | メモリ[0] | メモリ[4] | メモリ[3] | メモリ[7] |
| 5 | ミス | 5 mod 2 = 1 | メモリ[0] | メモリ[4] | メモリ[5] | メモリ[7] |
| 6 | ミス | 6 mod 2 = 0 | メモリ[0] | メモリ[6] | メモリ[5] | メモリ[7] |
| 7 | ヒット | 7 mod 2 = 1 | メモリ[0] | メモリ[6] | メモリ[5] | メモリ[7] |
| 0 | ヒット | 0 mod 2 = 0 | メモリ[0] | メモリ[6] | メモリ[5] | メモリ[7] |
5.20.5
未来にどのアドレスを参照するかを知ることはできないので、何が最適な置換かは誰にも分かりません。
5.20.6
ミス時にアドレスをキャッシュに格納するかどうか選べた場合、運が良ければ置き換えなかったアドレスをその後に参照してミス率が減るかもしれないですが、運悪く置き換えるはずだったアドレスをその後に参照してミス率が上がるかもしれません。
5.21
5.22
仮想記憶は、複数のアプリケーションを同時に動かすことができるように、仮想アドレスを利用します。
仮想マシンは、複数のOSマシンを同時に動かせるように、仮想アドレスを利用します。
(参考)
5.23
5.23.1
QEMUの欠点は以下から引用します。
CPUの命令単位でエミュレートする非常にプリミティブな仮想化方式のため,オーバーヘッドが大きくパフォーマンスが低下するのは避けられない。
この文章について、QEMUは多くの命令セット・アーキテクチャをエミュレートするためにオーバーヘッドが大きくなってしまう、という意味だと私は解釈しました。
本来の命令セット・アーキテクチャより速くなりうるかは分かりませんでした。
もしかすると、以下に言及されている命令列の組み合わせで、本来より速くなるのかもしれません。
QEMUでは命令の変換の際にあらかじめ用意した命令列をつなぎ合わせたり,変換結果をキャッシュに格納したりして高速化を図っている。
用語メモ
ライトスルー方式とライトバック方式
ライトスルー方式は、キャッシュに書き込む際に、主記憶装置にも同時に書き込む。
主記憶装置への書き込みには時間がかかるので、それが完了するのを待っていると性能が大幅に落ちてしまう。そこでライト・バッファにデータを一時保存しておき、主記憶装置への書き込みが完了時にライト・バッファのデータを解放する。
キャッシュとライト・バッファに書き込みすれば、主記憶装置への書き込みが完了していなくても処理を進められる。
ライトバック方式は、キャッシュのみに書き込み、主記憶装置にはキャッシュミスで置き換えが必要になった時に書き込む。
(キャッシュへの書き込み時、キャッシュが満杯の場合やタグが一致しない場合はキャッシュミスとなり、キャッシュは置き換えられる)
この方式の欠点として、不意に電源が消えるなどして主記憶装置のメモリが更新されずに終了してしまうと、主記憶装置とキャッシュの同じアドレスのデータが一致しなくなる恐れがある。
タグのサイズと連想度
4096ブロックのキャッシュ
ブロック・サイズは4語
アドレス32ビット
ブロックあたりのバイト数 32ビット/8ビット × 4語 = 16バイト = $2^4$バイト
インデックスとタグに使用されるビット数 32 - 4 = 28
ダイレクトマップ方式は、セット数とブロック数は同じなのでインデックスに使用されるビット数は$4096 = 2^{12}$より12ビット
よってタグに使用されるビット数は$(28-12)*4096=66,000$ビットになる。
2ウェイ・セット・アソシアティブ方式の場合は、セット数は半分になり、インデックス用のビットが1つ減り、タグ用のビットが1つ増える。
よってタグに使用されるビット数は$(28-11)*4096=70,000$ビットになる。
4ウェイ・セット・アソシアティブ方式の場合は、セット数は1/4になり、インデックス用のビットが2つ減り、タグ用のビットが2つ増える。
よってタグに使用されるビット数は$(28-10)*4096=74,000$ビットになる。
フル・アソシアティブ方式の場合は、セット数は1個であり、インデックスは不要で、タグに使用されるビット数は$28*4096=115,000$ビットになる。


