12月11日、胃にいい日。
変な事書いてツッコミを受けないかと胃をキリキリさせながら記事を書いております。
導入
ピアノにおいて響板という部位があり、これが弦から出る音を増幅させているいわば天然のアンプである。
 YAMAHA ピアノのしくみ 音が出るしくみより引用
YAMAHA ピアノのしくみ 音が出るしくみより引用
物理習いたての頃の私はこれが不思議だった。
アンプというアナロジーで考えると、エレキギターのアンプは電力をエネルギーとして供給することで音を増幅させている。しかし、響板はただの板で外部からエネルギーを供給しているわけでないのに音を増幅させている。
エネルギーの採算どうなってんねん と。
この記事では以下の2点について論じていこうと思う。
- 響板が音を増幅させる仕組み
- エネルギーの採算
※エネルギー保存と書いてないのは減衰振動やら音の伝搬やらを考えていてエネルギー保存と書くと面倒なことになりそうだったため。
響板が音を増幅させる仕組み
結論から言うと、響板はアンプのような"増幅装置"ではなく、弦と結合振動系をなす振動子 で、弦よりも良い放射能力 を持つためわれわれに効率よくエネルギー音として伝えてくれるものである。昔の私にとって「弦から出る音を増幅させている」という表現がミスリードであったのだ。
結合振動系の運動方程式を考えて解析的に振動の特性を...という議論は今回飛ばす。(インピーダンスマッチングについて見ておくと理解が深まると思うが見なくてもよい)
放射能力について詳しくまとめることで大学物理成分を加えていく。
音の球面波(準備)
音は疎密波で、圧力の振動ととらえることができるので以下の式を満たす。
\Delta p=\frac{1}{c^2}\frac{\partial^2 p}{\partial t^2}
導出はそこらにごまんとあると思うので省略。
$p=e^{i\omega t}P(\boldsymbol{r})$の形で表されるとすると
\Delta P+\frac{\omega^2}{c^2}P=0
の形になる。以降$\frac{\omega}{c}=k$とする。(いわゆる波数)
今回球対称な場合を考えるのでラプラシアンを極座標で書いて
\displaylines{
\Delta P&=&
\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial P}{\partial r})
+\frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta\frac{\partial P}{\partial \theta})
+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 P}{\partial \varphi^2} \\
&=&\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial P}{\partial r})
}
(球対称だと$\phi$は$\varphi,\theta$によらない)
$P=\frac{\phi}{r}$とすると簡単になって
\frac{\partial^2 \phi}{\partial r^2}+k^2 \phi=0
$p$についての解は
p=\frac{A}{r}e^{i(\omega t-kr)}+\frac{B}{r}e^{i(\omega t+kr)}
この状況は点音源から放射状に音が伝搬する様子を表す。
以降の議論に必要な概念をまとめておく。
音が疎密波であることを考えると流体の速度と圧力は以下の式を満たす。
\rho\frac{\partial u}{\partial t}=-\frac{\partial p}{\partial r}
$\rho$は媒質の密度である。(圧力についての波動方程式を求めるところで出てくる)先ほど導出した$p$の進行波だけを取って上の式に代入し、$u$を求めると
u=\frac{A}{r\rho c}(1+\frac{1}{ikr})e^{i(\omega t-kr)}
半径aの小さな球殻について体積速度Qという量を以下で定義し
Q=4\pi a^2 u(a)
$ka<<1$的な奴だの時を考えて$u$の式に代入してAを求める。
A=Q\frac{ikc \rho}{4\pi}e^{i\omega t}
$p$はこれを用いて ($\omega=kc$に注意)
p=Q\frac{i\omega \rho}{4\pi r}e^{-ikr}
となる。Qは"音荷"とでもいうべきもので、電磁気でいう電荷や磁荷みたいなものだ。(monopoleが話題の昨今だが...)
線音源による放射
本旨とはずれるが線音源の放射特性について記す。線音源の放射特性は双極子からの放射と類似している。これは高次モード(基本振動の整数倍での振動)で振動する弦が
+-+-+-+-+-+-+-+-+-+-+-+-.....
と節を挟んで逆相で振動し、逆相の音源が隣同士の状態ととれるためである。
双極子の放射がどうなっているか詳しく見ていこう。下図のような状況を考えて
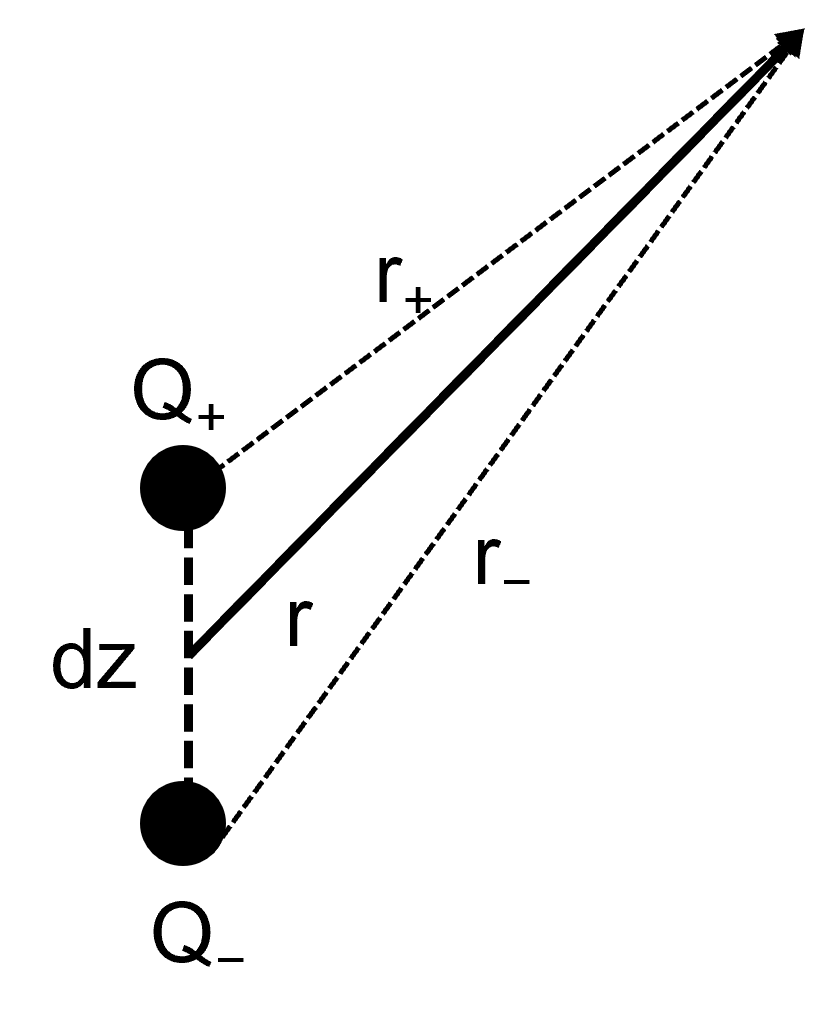
p_{\pm}=Q\frac{i\omega \rho}{4\pi}(\frac{e^{-ikr_+}}{r_+}-\frac{e^{-ikr_-}}{r_-})
$dz\rightarrow 0$をとる時、$r_+=r-\frac{1}{2}dz\cos\theta,r_-=r_++dz\cos\theta$として($\theta$は$dz$と$r$の角度)として$dz$周りのTalor展開を1次まで用いると
p_{\pm}=-Qdz\frac{i\omega \rho}{4\pi}(\frac{\partial\frac{e^{-ikr}}{r}}{\partial r})
$Qdz\rightarrow\mu$とするいつもの操作を行って、
p_{\pm}=-\mu\cos\theta\frac{\omega^2 \rho}{4\pi cr}(1+\frac{1}{ikr})e^{-ikr}
(なんか本と符号が合わない...。本旨ではないところだが。)
音響インテンシティという値が以下の式で表され、
I=\rho cu^2=\frac{p^2}{\rho c}
これはエネルギー流密度を表す。放射能力を評価するのによく使われる値だが双極子の$I$は十分遠方で
I=\frac{\omega^4\rho\mu^2}{16\pi^2c^3}\cos^2\theta
これから読み取るべきは双極子は$\omega$が小さいと放射能力が低い、双極子モーメントの方向の放射が強いという指向性を持つの2点である。
線音源に関する話は論文レベルで読み切れない書き切れないので結果だけ言うと
I\simeq(\frac{\pi\rho\omega^3a^4u^4}{4c^2r})\cos^2\theta
$a$はこの時線を円柱と見たときの半径である。双極子と似ている上に、とても小さい$a$の4乗に比例していて放射能力が著しく低いことがわかる。
囲まれた面音源による放射
つかれたので結果だけ。半径aの枠に囲まれた振動板or膜を考えると
p\simeq\frac{1}{2}i\omega\rho ua^2(\frac{e^{ikr}}{r})[\frac{2J_1(ka\sin\theta)}{ka\sin\theta}]
$u$は面の振動方向への速度、$J_1$は一次のBessel関数である。(これが円形ピストンと呼ばれる最も単純なモデルであることは一応断っておく)
$\omega$依存性が線よりも弱く、放射を弱める因子も特段ない。
余談だが、面音源の議論はBessel関数をはじめStruve関数など特殊関数マシマシなのでなかなか面倒 面白い。
これで大まかに面音源のほうが線音源よりも良い放射能力があることを示せた。
エネルギーの採算
振動弦のエネルギーは①空気抵抗 ②内部減衰 ③他系へのエネルギー伝搬 によって減っていく。①②③ともに減衰項(速度に依存する項)に現れ、運動方程式を見ればわかるように
\displaylines{
\frac{dx^2}{dt^2}+2\frac{1}{\tau}\frac{dx}{dt}+\omega^2x=0 \\
x=A\exp(-\frac{t}{\tau}+D)
}
減衰時間の逆数に比例する。(減衰時間は振幅が1/eになる時間)
力は線形であることから、減衰時間の逆数も線形である。
よって
\frac{1}{\tau}=\frac{1}{\tau_1}+\frac{1}{\tau_2}+\frac{1}{\tau_3}
$\tau_1,\tau_2,\tau_3$はそれぞれ①②③の要因による減衰時間である。弦が響板と離れている場合は$\tau_3$が消える。(伝搬で抵抗力が生じるとは何ぞやと感じた方はアドミッタンスで検索)
つまり弦が響板とつながっている場合$\tau$は減少し、減衰が早くなる。
振動エネルギーが早くなくなっていく ことで採算が取れていたのである。
あとがき
振動現象を電気回路とのアナロジーで考えることがあったり、今回の点音源の扱いが点電荷を扱った時と似ている議論をしていたり、電磁気色々便利だと感じた。
今回のテーマは高校の時に部活で研究していたもので高校の自分に向けたつもりで書いた。高校の時よりいろいろわかるようになってて楽しかった。
参考文献
楽器の物理学 丸善出版
N.H.フレッチャー/T.D.ロッシング[著] 岸憲史/久保田秀美/吉川茂[訳]