はじめに
この記事では遺伝的アルゴリズムについて説明する。初めにどのようなアルゴリズムなのか説明し、そこで紹介した操作を小分けにpythonでnumpyのみを使って実装する。遺伝的アルゴリズムというだけのことがあって高校の生物基礎程度の知識があると理解が容易にできる。
遺伝的アルゴリズム
遺伝子アルゴリズムは進化論の考え方に基づいたアルゴリズムで、データ(表現型)を遺伝子(遺伝子型)のように変形し選択や交叉、突然変異などの操作を繰り返すことによって最適な解を捜索するアルゴリズムである。表現型は遺伝子の評価などに使用し、遺伝子型は操作の対象として使われる。
フローチャート
厳密ではないがフローチャートは以下のようになる。Typoraでうまい作り方がわからず、随分下手なものになってしまったので参考程度に。
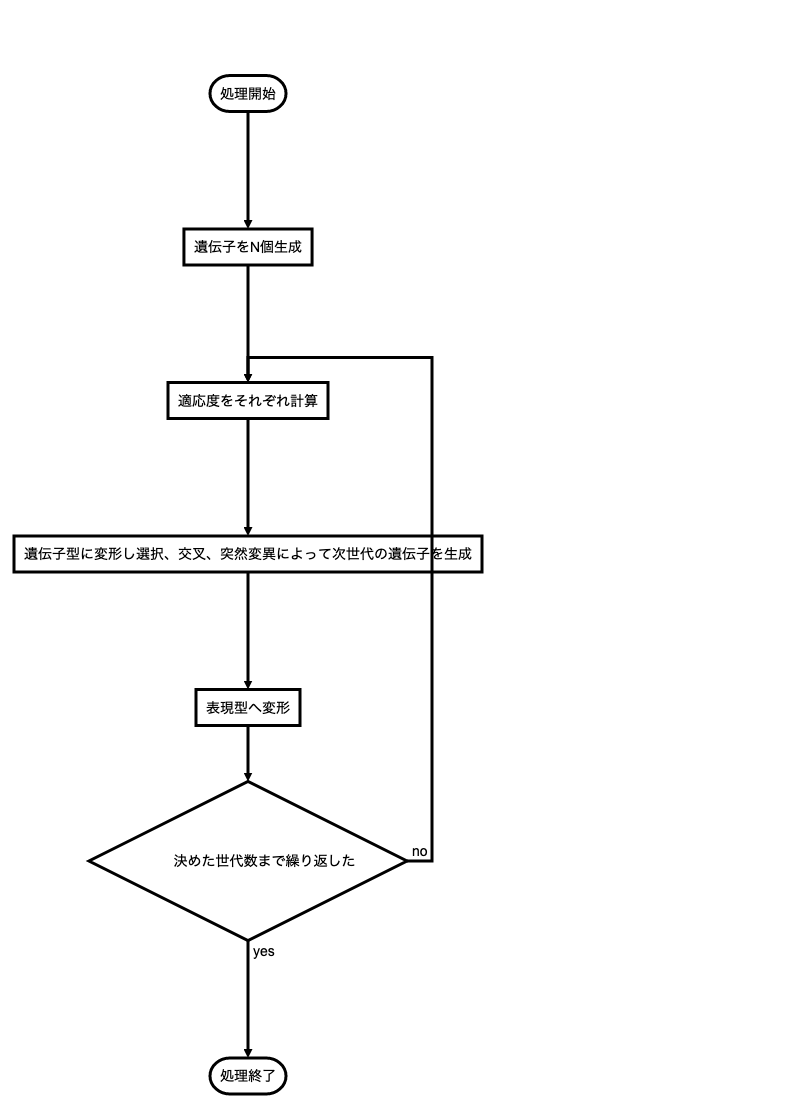
決められた世代までとあるが、評価がある閾値を超えるまで繰り返しを行うケースもある。また、遺伝子アルゴリズムでは最後に求められた解が最適な解とは限らないので過去も含め最も評価が良かったものを採用することもある。
遺伝子操作
次世代の遺伝子を生成する時、選択、交叉、突然変異の三つの動作のうちどれかを行う。それぞれが起きる確率の合計は1であり、交叉が起こる確率は突然変異よりもとても大きくすると良い。選択は学習、交叉と突然変異は捜索を行っていると考えられる。なので、交叉や突然変異を選択する確率は世代が進むにつれて小さくするとより良い結果を得られると考えている(私の意見なので参考程度に)。
選択
適応度を用いて優秀な遺伝子を増やしたり劣等な遺伝子を減らしたりする操作である。選択法にはルーレット選択、ランキング選択、トーナメント選択、エリート保存選択などがある。
ルーレット選択
ある確率$p_i$によって個体$i$を選択する方法である。確率$p_i$は個体の適応度によって決まり、以下のような式で表される。
$$
p_i = \frac{f_i}{\sum f_j}
$$
この選択法は適応度が負の場合を考慮しない方法で、遺伝子間の適応度の差が大きいときは適応度の高い個体ばかりが選ばれることによって収束が早期に起きてしまうと言う問題がある(私の考えだが、前者はexpで和取れば解決できるのではと考えている)。
ランキング選択
適応度の大きさでソートし、その順番によってあらかじめ与えた確率で選択する方法である。なるべくシンプルな実験をしたいときはこの選択方法が採用される。あらかじめ与えられた確率で計算するので、適応度の差による確率の違いが出ない。これによって早期収束の問題はないが、適応度の差が極めて小さい場合も確率が大きく変わることがある。また、ソートを選択の都度行わなければならないので計算コストが高くなる。
トーナメント選択
集団から決まった個数だけランダムに遺伝子を選び出し、その中で最も適応度の高い遺伝子を選択するこれを元の遺伝子個数回行う方法である(選ばれた遺伝子は次世代の遺伝子となり、その後の選択に影響はない)。選び出す個数はパラメーターであり、大きくすることで適応度の大きい遺伝子が次世代に増えるが、その場合早期収束する可能性が高まる。
エリート保存選択
エリート保存選択はこれまで紹介した選択法と組み合わせて使う選択法である。これは、適応度の大きさでソートし上位幾つかの遺伝子を次世代の遺伝子としてあらかじめ残すのようにする方法である。世代数を小さく収束した解を得たいときに使われる手法であり、局所的な解に収束しやすくなることや、ソートしなければならない問題がある。
交叉
遺伝子間で染色体を組み替えることによって次世代の個体を生成する操作であり、生物の交配によって子孫を残すことをモデル化したものである。一般的には一点交叉、二点交叉、多点交叉、一様交叉などが使われる。この記事では多点交叉については説明しない(二点交叉より良い値が出ることが少なく使うメリットがほとんどないから)。
一点交叉
最初に提案された交叉で遺伝子を入れ替える場所を一つ決め、それ以降を入れ替える方法である。効率が悪いため、現在はあまり使われない。
例 |は決めた場所
遺伝子1: 10101|001 => 次世代1: 10101100
遺伝子2: 01110|100 => 次世代2: 01111001
二点交叉
遺伝子の入れ替えの始点と終点を決め、その間の染色体を入れ替える方法である。
例 |は決めた場所
遺伝子1: 1010|101|0 => 次世代1: 10100100
遺伝子2: 1010|010|0 => 次世代2: 10101010
上の例で最適解が10101110であるとき入れ替えによって最適となる確率は$\frac{2}{8(8-1)}=\frac{1}{28}$である。8は遺伝子のサイズであり、これが大きくなると最適解が得られる確率が小さくなってしまう。この性質をヒッチハイキングという。
一様交叉
遺伝子の染色体をそれぞれ$\frac{1}{2}$の確率で入れ替える方法である。二点交差で求められなかった(求めにくかった)問題に使うと有効なことが多い(逆も然り)。
例 |は決めた場所
遺伝子1: 10101010 => 次世代1: 10100010
遺伝子2: 10100100 => 次世代2: 10101100
二点交差ではヒッチハイキングの問題があったが、一様交差では最適となる確率は$\frac{2}{2^3}=\frac{1}{4}$となり遺伝子のサイズに依存しないのでこの問題は発生しない。
突然変異
任意で染色体の一部の値を反転させる操作である(2進数の場合、数値だとランダム)。これによって局所的な解に収束することがなくなる。先にも述べたが、突然変異を起こす確率は他の操作(特に選択)と比べるととても小さい。なぜなら頻繁に突然変異を起こしているとランダムに次世代の遺伝子を生み出しているだけであり、最適な解を得られないからである。通常0.1~1%で設定される。
実装
遺伝子数が$N$、遺伝子の長さが$length$、遺伝子は0または1の値を取る染色体で構成されているとして実装する。
紹介するコードを実行したいときは以下でサンプルを利用すると良い(他の変数は適宜追加)。
N = 10
length = 8
gene_arr = np.random.randint(2, size=length)
fitness_arr = np.random.rand(N)
表現型と遺伝子型
表現型は遺伝子の適応度を計算するにあたって使用する型、遺伝子型は操作するにあたって使用する型である。表現型は一般的に10進数のように我々にも評価がわかりやすい型で、遺伝子型は2進数のようにわかりにくい型であることが多い。例えば関数の最大化なのでは実際その通りで、表現型として10進数、遺伝子型として2進数と変形して計算する(変形は2進数から10進数のみ)。2進数から10進数への変換だが、その場合のコードは以下のようになる。
def geno2pheno(gene_arr):
"""
遺伝子型から表現型への変換
Attributes
----------
geno_tabel: ndarray
表現型へ変更するためのテーブル
Parameters
--------------
gene_arr: ndarray
遺伝子
Returns
----------
表現型の遺伝子
"""
geno_table = np.array([2**i for i in range(length)])
return np.sum(gene_arr * geno_table, axis=1) / (2 ** length - 1)
長さlengthによって表現型の大きさが変わらないように正規化する。
## 選択
選択の引数としてchoice_numを導入した。理由はエリート保存選択で次世代の遺伝子を先に決めた時とエリート保存選択を行わなかった時では選択数が異なるからだ。choice_num+fix_num=Nの条件が課せられている。
ルーレット選択
def roulette_choice(gene_arr, fitness_arr, choice_num):
"""
ルーレット選択
Attributes
-------------
idx: ndarray
次の世代に選ばれた遺伝子のインデックス(重複可)
Parameters
--------------
gene_arr: ndarray
遺伝子
fitness_arr: ndarray
適応度が格納された配列
choice_num: int
選択する遺伝子数
Returns
----------
次世代の遺伝子
"""
idx = np.random.choice(np.arange(N), size=choice_num, p=fitness_arr/sum(fitness_arr))
return gene_arr[idx]
np.random.choiceの引数pは確率であり渡す配列は合計が1でなければいけない。そのため適応度fitness_arrその合計で割る必要がある。
ランキング選択
def ranking_choice(gene_arr, fitness_arr, prob_arr, choice_num):
"""
ランキング選択
Attributes
-------------
idx: ndarray
次の世代に選ばれた遺伝子のインデックス(重複可)
Parameters
--------------
gene_arr: ndarray
遺伝子
fitness_arr: ndarray
適応度が格納された配列
prob_arr: ndarray
あらかじめ与えられた確率(適応度順)
choice_num: int
選択する遺伝子数
Returns
----------
次世代の遺伝子
"""
gene_rank = np.argsort(fitness_arr)
idx = np.random.choice(np.arange(N), size=choice_num, p=prob_arr)
return gene_arr[gene_rank][idx]
トーナメント選択
def tournament_choice(gene_arr, fitness_arr, choice_num):
"""
トーナメント選択
Attributes
-------------
next_gene_arr: list
次世代の遺伝子
idx_chosen1: int
ランダムに選ばれたインデックス
idx_chosen2: int
ランダムに選ばれたインデックス
choice_num: int
選択する遺伝子数
Parameters
--------------
gene_arr: ndarray
遺伝子
fitness_arr: ndarray
適応度が格納された配列
Returns
----------
次世代の遺伝子
"""
next_gene_arr = []
for i in range(choice_num):
[idx_chosen1, idx_chosen2] = np.random.randint(N, size=2)
if fitness_arr[idx_chosen1] > fitness_arr[idx_chosen1]:
next_gene_arr.append(gene_arr[idx_chosen1])
else:
next_gene_arr.append(gene_arr[idx_chosen2])
return np.array(next_gene_arr)
エリート保存選択
def elite_choice(gene_arr, fitness_arr, fix_num):
"""
エリート保存選択
Attribute
-----------
gene_rank: ndarray
遺伝子を適応度順に並び替えたときのインデックス
Parameters
--------------
gene_arr: ndarray
遺伝子
fitness_arr: ndarray
適応度が格納された配列
fix_num: int
次世代に残す遺伝子数
Returns
----------
次世代の遺伝子
"""
gene_rank = np.argsort(fitness_arr)
return gene_arr[gene_rank][:fix_num]
## 交叉
一点交叉
def one_point_crossing(gene_arr, cross_point):
"""
一点交叉
Attribute
-----------
idx_chosen1: int
ランダムに選ばれたインデックス
idx_chosen2: int
ランダムに選ばれたインデックス
gene2: ndarray
二つ目のインデックスの遺伝子をコピーしたもの
Parameters
--------------
gene_arr: ndarray
遺伝子
cross_point: int
入れ替える場所を示す数字
Returns
----------
次世代の遺伝子
"""
[idx_chosen1, idx_chosen2] = np.random.randint(N, size=2)
gene2 = gene_arr[idx_chosen2].copy()
gene_arr[idx_chosen2][cross_point:] = gene_arr[idx_chosen1][cross_point:]
gene_arr[idx_chosen1][cross_point:] = gene2[cross_point]
return gene_arr
二点交叉
def two_point_crossing(gene_arr, begin_point, end_point):
"""
二点交叉
Attribute
-----------
idx_chosen1: int
ランダムに選ばれたインデックス
idx_chosen2: int
ランダムに選ばれたインデックス
gene2: ndarray
二つ目のインデックスの遺伝子をコピーしたもの
Parameters
--------------
gene_arr: ndarray
遺伝子
begin_point: int
入れ替える場所を示す数字(始点)
begin_point: int
入れ替える場所を示す数字(終点)
Returns
----------
次世代の遺伝子
"""
[idx_chosen1, idx_chosen2] = np.random.randint(N, size=2)
gene2 = gene_arr[idx_chosen2].copy()
gene_arr[idx_chosen2][begin_point: end_point] = gene_arr[idx_chosen1][begin_point: end_point]
gene_arr[idx_chosen1][begin_point: end_point] = gene2[begin_point: end_point]
return gene_arr
一様交叉
def uniform_crossing(gene_arr):
"""
一様交叉
Attribute
-----------
idx_chosen1: int
ランダムに選ばれたインデックス
idx_chosen2: int
ランダムに選ばれたインデックス
gene2: ndarray
二つ目のインデックスの遺伝子をコピーしたもの
Parameters
--------------
gene_arr: ndarray
遺伝子
Returns
----------
次世代の遺伝子
"""
[idx_chosen1, idx_chosen2] = np.random.randint(N, size=2)
gene2 = gene_arr[idx_chosen2].copy()
for i, chomosome in enumerate(gene2):
if np.random.rand() < 0.5:
gene_arr[idx_chosen2][i] = gene_arr[idx_chosen1][i]
gene_arr[idx_chosen1][i] = chomosome
return gene_arr
突然変異
突然変異は確率がいろいろ出てくるので整理する。まず、下記のコードにはない突然変異の操作をする確率。次に突然変異を起こすとき遺伝子が突然変異を起こす確率。最後に遺伝子が突然変異を起こすとして選ばれた時、染色体が突然変異を起こす確率である。
def mutation(gene_arr, gene_rate, chromosome_rate):
"""
突然変異
Parameters
--------------
gene_arr: ndarray
遺伝子
gene_rate: double
遺伝子が突然変異を起こす確率
chromosome_rate: double
染色体が突然変異を起こす確率
Returns
----------
次世代の遺伝子
"""
for i, gene in enumerate(gene_arr):
if gene_rate > np.random.rand():
for j, chromosome in enumerate(gene):
if chromosome_rate > np.random.rand():
gene_arr[i, j] = 1 - chromosome
return gene_arr
以上のものを組み合わせることで遺伝的アルゴリズムのコードを書くことができる。それを書くと長すぎるのでここでは省略する。
まとめ
遺伝的アルゴリズムは生物の進化システムを模倣したようなアルゴリズムで、選択、交叉、突然変異などの操作を繰り返すことによって最適解に近い解を見つけることができる。選択、交叉、突然変異などはそれぞれ次世代の遺伝子を作り出すための操作であり、選択、交叉で学習を行い突然変異で捜索を行うようなアルゴリズムであった。