はじめに
ベイズの定理について条件付き確率から順を追って説明する。また、理解の助けとなると考えられる具体的な例を2つ紹介する。
確率
この記事では確率を以下のように書く。
- 事象Aが起きる確率を$P(A)$
- 事象Aと事象Bが起きる確率を$P(A\cap B)$
- 事象Aまたは事象Bが起きる確率を$P(A\cup B)$
条件付き確率
ベイズの定理を説明する前に条件付き確率について説明する。条件付き確率とは事象Bが起きたという条件下で事象Aが起きる確率のことを指す。この確率は一般的に$P(A| B)$と書かれる。式で表すと以下のようになる。
$$
P(A|B) = \frac{P(A\cap B)}{P(B)}
$$
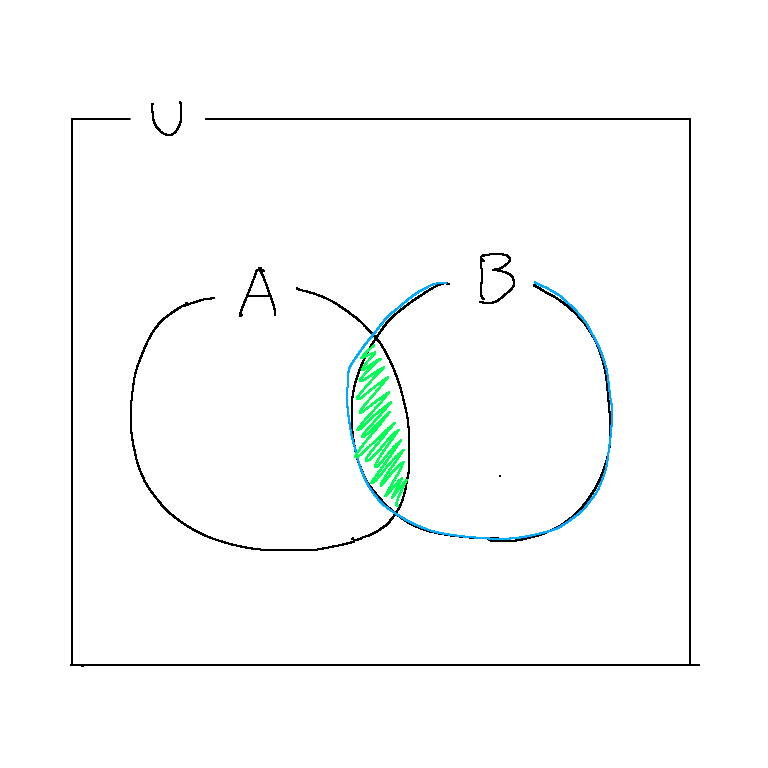
これは以下の弁図で考えると、青で囲まれた部分を緑色の部分で割った式である。
ベイズの定理
事象Bが起きたという条件の下で事象Aが起きる確率は
$$
P(A|B) = \frac{P(A\cap B)}{P(B)}
$$
でかけることを先ほど確認した。この逆(事象Aが起きたという条件の下で事象Bが起きる)の確率も同様に
$$
P(B|A) = \frac{P(A\cap B)}{P(A)}
$$
と書くことができる。また、これを変形して$P(A|B)$を用いて書こうとすれば以下のようになる。
$$
P(B|A) = \frac{P(A|B)P(B)}{P(A)}
$$
この式をベイズの定理と呼ぶ。事象Bが原因で事象Aが起きるという「原因->結果」の関係があるとき、$P(B|A)$は結果が事象Aとわかっている時に原因として事象Bが起きる確率である(説明がわかり辛いので具体例をのちに紹介する)。この確率は直感的に求めるのが難しいが、左辺を見ると$P(A|B),P(A),P(B)$のように直感的にわかる式で構成されているのでそれらの組み合わせて求めることができるという利点がある。直感的というのは現実の流れのような順番で考えられる確率のことを言った。
例1
ベイズの定理のわかりやすい例としてよく、病気の検査が使われるのでそれを採用して紹介する(PCR検査にも当てはまるホットな話題ということもある)。
罹患率が0.01%の病気で、検査の判定は以下のようなものを考える。
| 陽性 | 陰性 | |
|---|---|---|
| 罹患 | 95% | 5% |
| 非罹患 | 20% | 80% |
| 確率表記として |
- 罹患している確率を$P(B_1)=0.0001$
- 罹患していない確率を$P(B_2)=0.9999$
- 陽性である確率を$P(A_1)=0.95\times 0.0001 + 0.20\times 0.9999=0.200075$
- 陰性である確率を$P(A_2)=0.05\times 0.0001 + 0.80\times 0.9999=0.799925$
と書く。理想的な病気の検査では罹患したことが原因となって検査で陽性という結果がでる。罹患したことで検査で陽性がでる確率は表から$P(A_1|B_1)=0.95$である。これをもとに陽性と判定された人のうち実際に罹患している確率を求めることができる。その確率は$P(B_1|A_1)$であるのでベイズの定理を使って$P(B_1|A_1)=\frac{P(A_1|B_1)P(B_1)}{P(A_1)}=0.00047482$となる。この例では罹患している人が陽性と出る確率(真陽性率)が高いので検査がもっともらしいものに感じるが、計算すると陽性と出ても0.05%しか実際に罹患していないことがわかる(再検査の重要性)。ここで出てきた数値は適当に設定したものである。
例2
ベイズの定理が有効な場面として有効な場面としてモンティ・ホール問題がある。問題の設定は以下のようなものである。
- 当たりが入った箱1つとハズレが入った箱を2つ準備する
- 3つの箱から一つを選ぶ。箱の見た目は全て同じで当たりである確率は$\frac{1}{3}$である。
- 残った二つの箱のうち一つを指定してそれがハズレという情報を与える。
- その後箱をもう一度選ぶチャンスを与えると、最初選んだ箱が当たりである確率が$\frac{1}{3}$、残った箱に当たりである確率が$\frac{2}{3}$となる。
これは直感的に残った箱二つの箱から選ぶので確率は$\frac{1}{2}$や、三つのうち一つを選んでいるので選び直したとしても$\frac{1}{3}$と考える人が多いが、選び変えた時の確率は$\frac{2}{3}$であるというパラドックスとして有名である。
この例ではハズレという情報が開示された(原因)下で、選んだ箱が当たりである確率(結果)を求める。箱1を選ぶ確率を$P(A_1)$、箱2を公開する確率を$P(B_2)$と書くとする。選んだ箱が当たりである確率は定義より$\frac{1}{3}$、箱1を選んでいた場合は箱2または箱3を公開する選択肢しかないので箱2を公開する確率は$\frac{1}{2}$である。箱1を選び、それが当たりの場合を考える。この場合$P(B_2|A_1)=P(B_3|A_1)=\frac{1}{2}$となる。箱2が当たりの時は$P(B_2|A_1)=0, P(B_3|A_1)=1$となる。箱3が当たりの時も同様。箱1,2,3には区別がないので、入れ替えた値は変わらない。
箱2を開示した下で最初に選んだ箱1が当たりの確率$P(A_1|B_2)$求める。ベイズの定理より
$$
P(A_1|B_2)=\frac{P(B_2|A_1)P(A_1)}{P(B_2)}
$$
となる。このとき、$P(B_2|A_1)=\frac{1}{2},P(A_1)=\frac{1}{3},P(B_2)=\frac{1}{2}$より、$P(A_1|B_2)=\frac{1}{3}$となる。次に最初に箱1を選び、箱2を開示した下で箱3が当たりである確率$P(A_1|B_2)$を求める。先程同様にベイズの定理より
$$
P(A_1|B_2)=\frac{P(B_2|A_1)P(A_1)}{P(B_2)}
$$
となる。先程同様に$P(B_2|A_1)=1,P(A_1)=\frac{1}{3},P(B_2)=\frac{1}{2}$より$P(A_1|B_2)=\frac{2}{3}$となる。
これより、箱を選び直した時の確率が$\frac{2}{3}$となることが示された。